华志豪 郭琴 樊碧璇 谢旻

(江西师范大学物理与通信电子学院,南昌 330022)

在光力学系统中,辐射压力引起的非线性可导致系统产生混沌等多种丰富的动力学行为.从有序转变到混沌有各种各样的途径,本文研究了回音壁式耦合光力系统中两种不同途径通往混沌的现象——倍周期分岔道路和准周期道路.两个全同的光力学子系统通过光学倏逝波进行耦合,调控子系统间的耦合强度,可以有效地改变系统的动力学行为.采用分岔图、李雅普诺夫指数以及相空间轨迹的变化分析系统从有序到混沌的转变.研究表明,较强的耦合强度会迫使两个子系统的振荡产生完全同步,子系统间相互耦合的作用可等效于子系统光学模频率与外加控制场频率失谐量的增加,耦合光力学系统的动力学行为等效于单个光力学系统的动力学,可实现倍周期分岔道路通往混沌的转变.而对于相对较弱的耦合,耦合系统的动力学将在高维相空间展开,极限环发生Hopf 分岔,形成环面吸引子.选取合适的失谐量,耦合系统可实现从准周期道路进入混沌的现象.

1 引言

光力学系统[1]是研究光场和机械振子相互作用的典型模型.近年来,光力学系统的相关研究备受关注,已经成为量子光学、微纳光子学等多个领域的研究对象,并且在精密测量和量子信息处理等方面展现出重要的应用价值,呈现了丰富的物理现象,如机械振子的主动冷却[2,3]、量子纠缠[4,5]和类电磁诱导透明[6,7]等.

光力学系统中的辐射压力可以诱导多种非线性效应.在20 世纪八十年代,光力学系统中的双稳态就已被发现[8].近二十年来,随着腔的品质和性能不断提高,光力学系统中的非线性动力学得到了广泛研究,如动态多稳性[9,10]、随机共振[11,12]、耦合光力学系统中的同步效应[13,14]、魔鬼阶梯[15]、阿诺德舌头[16]等.

混沌是非线性动力学的一个重要分支,其实现机理是众多研究者关注的焦点.目前已在各领域实现了多种通往混沌的途径,如倍周期分岔道路[17,18]、准周期道路[19,20]及阵发性混沌道路[21-23]等.光力学系统因具有非线性也成为研究混沌的典型系统之一[24-29].在光力学系统中,通往混沌的道路大部分遵循倍周期分岔道路,由准周期道路通往混沌的现象鲜有研究.Roque 等[30]曾研究发现,在弱耗散的经典光力学系统中可产生准周期吸引子,实现从极限环到产生准周期运动,进而实现向混沌的转变.这为光力学系统中产生混沌现象提供了一种新的途径.另一方面,在连续系统中,非线性和三维及以上相空间是产生混沌的必要条件.高维相空间意味着更丰富的动力学行为[31].因此,耦合系统成为研究环面吸引子和高维混沌等动力学行为的自然候选者.在耦合系统中,环面吸引子为最常见的吸引子,但环面吸引子可能会随着参数的变化直接失稳,从而导致混沌,即产生由准周期道路通往混沌[31-35].关于耦合系统中产生准周期道路向混沌的转变,较早的研究可以追溯到Buskirk 和Jeffries[31]在电子电路中的实验,他们发现改变驱动电压时,电路中单一非线性谐振器表现为倍周期道路向混沌转变,而两个耦合的谐振器则表现为准周期道路向混沌转变.随后,有研究发现,在耦合Lorentz 系统[32,33]和耦合Duffing 振子系统[34]中不仅存在准周期运动,还存在稳定的三频准周期运动以及高维混沌等现象.

基于上述研究背景,本文利用光学倏逝波将两个回音壁式光力学子系统进行耦合,考虑两个光力学子系统的系统参数完全相同,研究耦合光力系统中的混沌动力学行为.研究发现,两个子系统间的耦合强度对于系统混沌运动的产生及其动力学过程有着重要的作用.当两个光力学子系统间的耦合较强时,强耦合将会导致两个子系统的动力学完全同步,两个子系统间耦合的作用等效于改变子系统中控制场与腔场的失谐量,耦合系统可实现传统的倍周期分岔通往混沌的现象.然而,对于两个子系统间弱耦合的情形,耦合系统的动力学将进入高维相空间,极限环发生Hopf 分岔,形成二维环面吸引子.在合适的失谐量下,调控耦合强度,可实现二维环面吸引子向奇异吸引子的转变,即从准周期运动通往混沌的转变.文中采用系统的分岔图和对应的李雅普诺夫指数谱进行详细分析,并展示了锁频这一经典动力学现象.

本文的总体安排如下: 第2 节介绍本文的研究模型——回音壁式耦合光力学系统,理论推导系统的运动方程,分析无耦合情形下子系统的稳态区域;第3 节讨论耦合光力学系统的非线性动力学行为,使用力学模振幅分岔图和最大李雅普诺夫指数联合进行分析,详细展示了耦合系统中倍周期分岔和准周期运动向混沌的转变行为;最后,第4 节进行了总结.

2 理论模型

本文研究的是回音壁式耦合光力学系统如图1 所示.两个光力学子系统a1和a2(频率分别为ω1和ω2)通过光学倏逝波耦合,并且两个子系统中分别包含频率为ωm1和ωm2的力学模.采用纤维型波导分别与两子系统的边侧耦合,用于控制场E1和E2(频率均为ωL)的输入与输出.

在旋转波近似下,该耦合系统的哈密顿量可表示为 (ℏ=1) :

考虑坏腔极限,即光学模与力学模之间的耦合系数远小于光场的衰变率,机械模式的零点涨落远小于对应光学模式的线宽,因此系统的量子涨落可以忽略不计.系统随时间演化的动力学方程可以表示为

通过线性化处理,可以得到系统的雅可比矩阵为如下形式:

其中αir和αii(i=1,2) 是腔中光学模复振幅的实部和虚部.雅可比矩阵的特征值可用于判断系统在平衡点的稳定性以及李雅普诺夫指数的计算.

图2 给出了两个子系统之间无耦合的情形下(G=0 ),系统处于稳态时,力学模的位置x1随失谐Δ1的变化曲线图.可以看出,随着失谐Δ1的增加,系统可由单稳态(蓝色区域)演化为自持振荡状态(绿色区域),然后再过渡到双稳区域.图中小框内曲线描述了系统从单稳态区域过渡到自持振荡区域的临界区域内雅可比矩阵特征值的复平面图.在该区域内,随着失谐的微小增加,雅可比矩阵将出现一对共轭特征值——ξ和ξ∗,两特征值的虚部跨越实轴,系统发生超临界Hopf 分岔,形成不稳定焦点,并同时产生一个稳定的极限环,系统开始自发振荡.

图2 两个子系统无耦合情形下,力学模的稳态位置 x1 随失谐 Δ1 的变化曲线图.蓝色表示稳定解,绿色表示参量不稳解,红色表示不稳定解.小框内为雅可比矩阵的一对共轭特征值虚根变化的复平面图.系统参数分别为κ1=1.0ωm1,γ1=0.26ωm1,g1=-0.0006ωm1,E1=2980ωm1Fig.2.System stability diagram of x1 with the varying of detuning Δ1 under uncoupling between the two subsystems.Blue stands for the stable branches,green stands for parametric instability,and red stands for unstable branch.The virtual rosots of a pair of conengenvalues for the Jacobi matrix are presented in the small box.The parameters areκ1=1.0ωm1,γ1=0.26ωm1,g1=-0.0006ωm1,E1=2980ωm1.

3 系统的混沌现象

3.1 倍周期分岔道路

本文考虑由两个全同光力学子系统构成的回音壁式耦合系统,即两个子系统具有完全相同的系统参数.当两个子系统间耦合强度较强时,可产生迫使两个子系统的振荡完全同步的情形[36,37].为了体现强耦合导致的同步现象,图3 给出了失谐Δ1=Δ2=-1.0ωm1时,不同耦合强度G下两个子系统力学模位置x1和x2的输出曲线,其中蓝实线为x1的输出曲线,红虚线为x2的输出曲线,系统各算符的初始平均值随机.不难发现,当耦合强度较弱时,两个子系统的输出并不同步,如 图3(a)和图3(b)所示.然而,在较强耦合下,两个子系统的位置输出曲线x1和x2在时域上完全重合,即子系统之间的振荡实现了完全同步,如图3(c)—(f)所示.而且在强耦合下,随着G的增加,系统的动力学行为也有显著改变,其输出从有序化的周期振荡逐步转变为无序化振荡.当两个子系统耦合强度为G=1.7ωm1,位置输出曲线为单周期振荡,如图3(c)所示,图中以黑色框标记单周期.继续增强耦合强度G,振荡周期也不断增大,由单周期振荡变为倍周期、四周期乃至无周期振荡.图3(f)中的无周期运动表明系统很可能已经进入了混沌状态.

图3 不同耦合强度下两个子系统力学模位置的输出曲线,蓝实线对应 x1 ,红虚线对应 x2 (a) G=1.0ωm1 ;(b) G=1.5ωm1 ;(c) G=1.7ωm1 ;(d) G=2.3ωm1 ;(e) G=2.8ωm1 ;(f) G=3.0ωm1 .两个子系统参数完全相同,初始条件随机,Δ1=Δ2=-1.0ωm1,其余参数和图2 相同Fig.3.Output curves of the two mechanical modes under different coupling strengthes.The blue solid line and the red dashed line correspond to x1 and x2 ,respectively: (a) G=1.0ωm1 ;(b) G=1.5ωm1 ;(c) G=1.7ωm1 ;(d) G=2.3ωm1 ;(e) G=2.8ωm1 ;(f) G=3.0ωm1 .The parameters for the two subsystems are exactly the same,and the initial conditions are arbitrary.All parameters are the same as those in Fig.2 except for Δ1=Δ2=-1.0ωm1 .

当系统在强耦合下迫使两个子系统达到完全同步时,两个子系统力学量的稳态值在任意时刻均相等,光学模的复振幅也不例外,即α1=α2.系统的动力学方程中(2)式可改写为

为了定量分析耦合系统的动力学行为,进一步给出了强耦合下x1的振幅随两个子系统间耦合强度变化的分岔图以及最大李雅普诺夫指数图,如图4 所示.李雅普诺夫指数是表示相空间相邻轨迹的平均指数发散率的数值指标.该指数越大,表示系统的局域稳定性越差,当其大于零时,则代表系统处于混沌状态.观察分岔图可以得知,随着耦合强度的增强,x1的振荡从单周期开始,随后周期逐步加倍,直至无周期振荡.对于无周期区域,最大李雅普诺夫指数λ1皆为正值,表明在这些区域,系统已经进入混沌状态.随着耦合强度的增加,系统的动力学行为的周期数倍增,直至进入混沌状态,这种现象被称为倍周期分岔,也是单个光力学系统中通往混沌最常见的途径[25].耦合系统的倍周期分岔路径的产生正是由于单个子系统在失谐的区域存在一个对应的倍周期分岔现象.强耦合的作用迫使两个子系统的振荡完全同步,因此耦合光力学系统的动力学行为等效于单个光力学系统,实现了倍周期分岔道路向混沌的转变.

图4 (a)系统倍周期分岔图;(b)最大李雅普诺夫指数图.所有参数和图3 相同Fig.4.(a) Schematic period-doubling bifurcation diagram;(b) the curve for the maximum of Lyapunov exponents.All parameters are the same as those in Fig.3.

3.2 准周期道路

接着,进一步考虑两个全同子系统间的耦合强度相对较弱的情形.强耦合可迫使两个子系统的动力学完全同步,耦合系统的动力学行为与单个子系统的维度相同,只在四维相空间展开,这被称为同步流形,而完全同步下出现的混沌可被称为同步混沌.在相对较弱的耦合下,子系统之间的振荡具有相干性,耦合系统的动力学行为将在高维相空间展开.此时,通过调节光学耦合强度,可诱导极限环发生超临界Hopf 分岔,产生环面吸引子,这为耦合系统产生准周期路径提供了先决条件.为了可观测到耦合系统的环面失稳,实现准周期路径通往混沌的转变,还需系统处于容易产生复杂动力学行为的参数区域范围内.倘若在合适的失谐量下,强耦合迫使两个子系统达到完全同步时,系统已经处于或接近处于同步混沌状态,那么这就为相对较弱耦合时产生环面失稳并通往混沌提供了可能.为此,选取失谐为Δ1=Δ2=0.5ωm1,调节耦合强度,研究耦合系统从准周期运动向混沌的转变.

图5 给出了两个子系统在失谐Δ1=Δ2=0.5ωm1时,不同耦合强度下系统的三维相空间图I1(a1腔光子数)-x1-p1的轨迹、二维相空间图x1-x2的 轨迹、李雅普诺夫指数谱以及x1的频率谱.为了体现混沌对初始条件的敏感度,图5 给出了两组初始条件下三维相空间图的轨迹,其中第一组初始条件是随机生成的,第二组初始条件与第一组的区别是初始的x1被增加了 10-5,图中利用两种不同颜色进行表征.其余三个子图只展示了系统为第一组初始条件下的结果.在无共存吸引子的情况下,系统在任意初始条件下的功率谱和李雅普诺夫指数谱的特征稳定.二维相空间则很好地体现了两个子系统动力学的关系.

图5 不同耦合强度下 系统 达到 稳定时的状态图 (a) G=1.47ωm1 ;(b) G=1.53ωm1 ;(c) G=1.60ωm1 ;(d) G=1.87ωm1 .其中每张子图中包含4 个分图,左上图对应 I1-x1-p1 三维相空间轨迹,两种颜色表征两组初始条件下的轨迹;左下图对应x1-x2二维相空间轨迹;右上图对应动态李雅普诺夫指数谱(前4 个李雅普诺夫指数);右下图对应 x1 的频率谱.Δ1=Δ2=0.5ωm1,其余参数和图3 相同Fig.5.Stability diagrams of the system under different coupling strengthes: (a) G=1.47ωm1 ;(b) G=1.53ωm1 ;(c)G=1.60ωm1 ;(d) G=1.87ωm1 .Each subgraph includes four charts,the top left one corresponding to the three-dimensional phase space of I1-x1-p1,and the two colors represented the traces for two sets of initial conditions;the bottom left one corresponding to the two-dimensional phase space of x1-x2 ;the top right one corresponding to Lyapunov exponents (the top four Lyapunov exponents);and the bottom right one corresponding to the frequency spectrum of x1 .The other parameters are the same as those in Fig.3 except for Δ1=Δ2=0.5ωm1 .

为了区分极限环和极限环面,借助李雅普诺夫指数谱来判断吸引子的类型.系统具有八维相空间,拥有8 个李雅普诺夫指数.在数值模拟中,从大到小排列,李雅普诺夫指数的第4 个值表现为稳定负值,因此图5 只给出了前4 个李雅普诺夫指数λi(i=1,2,3,4).当两个子系统间的耦合强度G=1.47ωm1时,三维相空间图显示吸引子为标准二维环面,如图5(a)所示.在李雅普诺夫指数谱中,λ1和λ2重合在 0 处,而λ3和λ4为负值,表明吸引子属于 (0,0,-,-,···) 型,对应二频准周期运动.而在x1的频率谱中,其主频峰ω01以左出现了一个不可公度的新频率ω02,谱中所有频率分量都可以表示为这两个基本频率的线性组合,这也是二频准周期运动的表征.当耦合强度增强到G=1.53ωm1时,如图5(b)所示,三维相空间图表明吸引子出现了分形结构的趋势,而李雅普诺夫指数λ1上升为正值,说明系统已经处于混沌状态.不难看出,即使两组在具有微小差别的初始条件下,三维相空间图有着完全不同的两组轨迹(两种不同的颜色表征),表明混沌对初始条件非常敏感,这是混沌的特点之一.然而整体上,两组轨迹又被限制于相同的区域,这是因为吸引是耗散系统的整体性质.相较于图5(a),x1的频率谱细峰逐渐消失,并且峰值也有所降低,此时系统刚刚过渡到混沌,混沌的特征还不够明显.继续增强耦合强度,G=1.60ωm1,如图5(c)所示,相较于图5(b),λ1明显上升,x1的频率谱展现出混沌的标准特征,即宽峰和类似噪声的整体谱线.三维相空间图出现了奇异吸引子的特征,即明显的分形结构.然而,当耦合强度达到G= 1.87ωm1时,x1-x2二维相空间图为一条关于x1-x2对称的直线,如图5(d)所示.这是两个子系统动力学行为完全同步在相空间的体现,过强的耦合强度导致子系统的振荡完全同步.结合李雅普诺夫指数(λ1的正值)以及与图5(c)类似的功率谱,说明此时耦合系统处于同步混沌的状态.

下面仍以x1的振幅随耦合强度变化的分岔图以及李雅普诺夫指数谱来详细分析系统从准周期道路向混沌的转变过程,图6 给出了系统的分岔图和李雅普诺夫指数图.x1的振幅分岔图中显示,随着耦合强度的增大,系统的动力学过程历经了极限环、准周期运动、有限周期运动以及由准周期运动向混沌状态的转变.当耦合强度G较小时,系统的振荡是单周期的极限环,其相应的李雅普诺夫指数谱中最大值λ1为零,λ2和λ3为相等的负值.随后,λ2和λ3开始分离,λ2上升至零并保持为零,而λ3则下降,依然为负值.这表明极限环发生了超临界Hopf 分岔,转变为稳定的二维环面[38],即准周期运动.x1的振幅变得稠密,而且x1的频率谱上将会出现两个不可公度的基本频率.随着耦合强度的增强,两个基本频率会发生微小移动.如果满足两个基本频率之比为有理数,系统将出现锁频现象,并且系统的动力学行为由准周期运动转变为有限周期运动.如此交替变化,两种动力学现象交替的间隔越来越小,直至系统完全处于准周期运动状态.然而继续增强耦合强度,系统将出现环面失稳,开始由准周期运动向混沌状态的转变,其标志是分岔图中下边界不再清晰.而系统处于混沌状态的另一标志是李雅普诺夫指数λ1急剧上升,变为大于零的正值,同时λ2上升至零的位置,在这个范围内吸引子拥有环面的形状,如图5(c)所示.当耦合强度过强时,系统的动力学行为再次出现了突变,李雅普诺夫指数谱也有一个明显的变化,λ3先上升为零,随后立刻下降为负值,与λ4基本保持相等.强耦合导致了两个子系统振荡完全同步,引起了同步混沌的现象,这与图5(d)所示结果完全符合.同步混沌的发生为耦合系统产生环面失稳给予了很好的解释.混沌往往发生于系统处于容易产生复杂动力学行为的参数区域内.虽然强耦合导致的同步混沌不是高维相空间的产物,但其发生区域依然是系统动力学剧烈变化的区域,并且具有鲁棒性.因此,调节光学耦合强度,使环面吸引子不断靠近同步混沌时,将会激起耦合系统产生复杂的动力学行为,从而产生环面失稳变为奇异吸引子,实现从准周期路径通往混沌的转变.

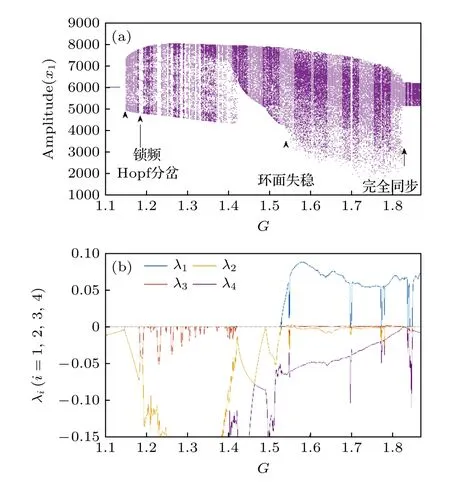
图6 (a)准周期路径分岔图;(b)李雅普诺夫指数图(前4 个李雅普诺夫指数).所有参数与图5 相同Fig.6.(a) Schematic quasiperiodic bifurcation diagram;(b) curves of Lyapunov exponents (the top four Lyapunov exponents).All parameters are the same as those in Fig.5.

4 结论

综上所述,本文利用光学倏逝波耦合两个回音壁式全同光力学子系统,从理论上研究了该耦合系统中两个子系统间的相互耦合对系统产生混沌现象的影响.调控两个光力学系统之间的耦合强度,耦合系统可实现倍周期分岔道路和准周期道路进入混沌的转变.倍周期分岔的产生原因是由于强耦合迫使两个子系统的振荡完全同步,使得在强耦合下调制耦合系统的耦合强度等效于改变了子系统光学模频率与外加控制光场频率的有效失谐量,耦合系统的动力学可退化为单个光力学系统的动力学过程,实现倍周期分岔通往混沌的道路.对于较弱的耦合,系统的动力学将进入高维相空间,极限环发生Hopf 分岔,形成环面吸引子.选取合适的失谐量,系统可实现环面失稳,从而产生从准周期道路进入混沌的现象.

感谢江西师范大学物理与通信电子学院段正路教授的讨论.