肖勇 曹雨生

(宁夏大学物理学院,银川 750021)

光波导模式分析是先进波导器件和光波线路设计中的一项基本任务.如何处理电磁异质界面和吸收边界问题是光波导高效数值分析面对的两大困难.现有高阶精度有限差分模式分析方法均未考虑吸收边界条件,导致漏模和辐射模难以精确模拟.本文基于浸入界面方法和完美匹配层吸收边界条件,提出一种具有二阶和四阶精度的有限差分方法.利用该方法对单界面等离子波导、平面对称波导和一维光子晶体波导进行模式分析,数值实验结果表明二阶和四阶算法对于导模、漏模和辐射模的收敛速度均与期望的阶数相符,二阶算法约在归一化步长 10-4 时提供有效折射率相对误差约为 10-9 的极限精度,四阶算法约在归一化步长10-3时提供有效折射率相对误差约为 10-10 的极限精度.对一维光子晶体波导中导模和包层模场分布进行的研究表明,界面处横电模式的场及其一阶导数的连续,横磁模式的场的连续及其一阶导数的不连续,均可以被精确解析.本文提出的方法只需利用折射率的值而不依赖于模场的特定函数表示,即可用于计算任意折射率剖面下的任意模式,为阶跃折射率平面波导模式分析提供一种简单而高效的工具.

1 引言

电磁异质结构对于集成光学和光纤光学中多数光子器件功能的实现至关重要.在先进波导器件和光波线路的设计中,光波导模式的全矢量求解是一项基本任务[1-3].在各种数值方法中,有限差分法(finite-difference method,FDM)易于实现而被普遍用于波导模式分析[4,5].有限差分法一般通过求解稀疏矩阵本征值问题可同时高效地确定多个模式的传播常数以及模场.波导存在折射率跳变的界面,导致模场及其导数一般是不连续的.标准有限差分法基于微分方程的解及其导数的连续性,直接应用于界面问题时,会降低差分格式的精度.针对界面问题的高精度有限差分求解,LeVeque 和Li[6,7]提出了浸入界面方法(immersed interface method,IIM),该方法可以系统地生成所需精度的差分格式.Horikis 和Kath[8-10]将IIM 应用于光波导模式分析,分别发展了具有任意截面形状二维波导的二阶精度算法以及光纤的二阶和四阶精度算法.在IIM 提出之前,Stern[11]利用泰勒级数展开模场然后匹配界面边界条件的方法,来改进阶跃折射率光波导模式分析的有限差分法.模场展开和匹配边界条件也是IIM 的两个基本步骤,IIM 和Stern方法仅在差分格式的系数修正如何表示方面存在微小差异,IIM 将系数修正表示为矩阵方程的解,Stern 方法直接给出系数修正的解析表达式.在Stern 工作的基础上,研究者经过二三十年的努力,最终开发出了光波导的全矢量任意阶精度模式求解器[12-18].高阶格式提供更快的收敛速度,极大降低计算资源需求,提高计算精度.然而在现有波导模式分析的高阶方法中,均未考虑吸收边界条件,需要设置较大的计算区域以令导模的倏逝场衰减至可用硬壁截断,而漏模则难以精确模拟.

本文针对阶跃折射率平面波导模式的全矢量求解,采用IIM 和完美匹配层(perfectly matched layer,PML)[19,20]吸收边界条件发展二阶和四阶精度的有限差分法,该方法对导模、漏模和辐射模均能高效模拟.本文的组织结构为: 第2 节列出发展算法所需的解析方程;第3 节详细推导二阶精度有限差分格式,四阶精度格式的推导与二阶精度情形类似,主要结果罗列在附录中;第4 节通过多种典型平面波导中各类模式的模拟,验证算法的有效性;第5 节给出结论.

2 基本方程

考虑如图1 所示的多层平行平面系统,每层填充各向同性介质.平行平面系统的模式分为横电(transverse electric,TE)和横磁(transverse magnetic,TM)偏振,非零场分量分别为(Ey,Hz,Hx)和 (Hy,Ez,Ex) .取时谐因子为 e-iωt,并令∂/∂y=0,TE 偏振满足的场方程为

图1 平面波导示意图及坐标系放置Fig.1.Depiction of a planar waveguide and layout of the coordinate system.

边界条件为Ey和Hz在界面处连续.TE 和TM 偏振有对偶关系,二者满足的场方程和边界条件在变换

下均互换.因此,可以先求解TE 偏振,TM 偏振的相应结果直接由对偶关系获得.

值得指出的是,经典电磁学中没有长度量纲的基本常数,麦克斯韦方程满足缩放不变性[21].这种缩放不变性在本问题中表现为,(5)式和(6)式中的空间坐标x和电磁波长λ均可收缩入归一化坐标.在将空间坐标归一化后,计算结果对于波导结构和波长满足相同比例关系的所有情形均适用.

3 算法

对于给定的平面波导结构,选取包含所有界面的计算区域,并用N个等间隔的格点将其离散,电场和磁场位于相同的格点,如图2 所示,其中竖线表示界面.记归一化空间步长为h,格点i的归一化坐标为.对于一般的第i个格点,用三点格式

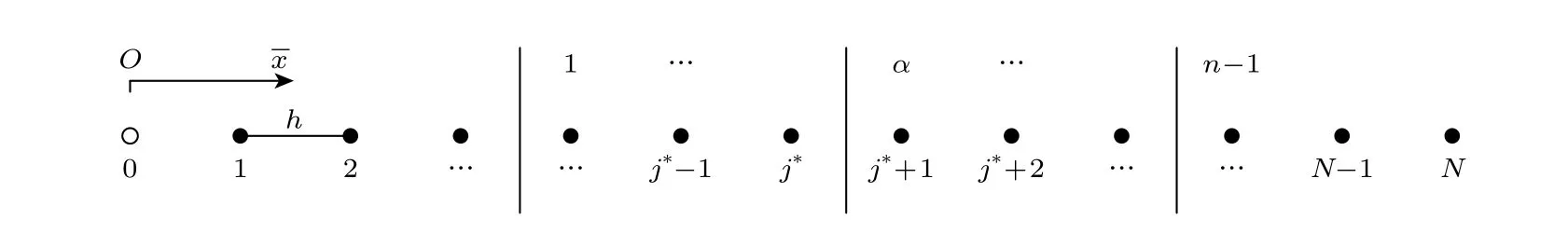
图2 计算区域离散Fig.2.Discretization of the computational domain.

近似波动方程(6).

3.1 常规格点

若格点i及其 邻近的两个格点i-1 及i+1 均在同一介质层内,则i为常规格点,对二阶导数取标准的中心差分格式近似将获得二阶精度,相应的差分方程(7)的系数为

3.2 非常规格点

对于如图2 所示的某一界面α两侧的格点j∗和j∗+1,三点格式跨越界面,由于E的一阶导数不连续,若依然采用(8)式作为差分方程(7)的系数,则全局精度一般降为零阶.格点j∗和j∗+1 称为非常规格点,相应的系数C±1,0需要修正以获得全局的二阶精度.

采用IIM 获得非常规格点处的修正系数C±1,0,需要E及其一阶和二阶导数在界面处的跳跃条件.引入记号 [f]=0 表示函数f在界面处连续,即f-=f+,其中“-”和“+”分别表示界面左侧和右侧.边界条件直接给出E的跳跃条件:

利用跳跃条件(9)—(11)式,将(14)式改写为

将(12)式、(13)式、(15)式和(19)式代入(20)式,并令(20)式等号右边O(h) 前的部分为零,得到

从中求得的C±1,0使得格点j∗处的局域截断误差为T=O(h),即局域一阶精度.由于界面比计算区域低一维,非常规格点具有局域一阶精度即可以保证算法的全局二阶精度[6].引入记号

类似地,可以求得非常规格点j∗+1 处的修正系数C±1,0满足的方程:将δ+-和µ+-的定义式(16)—(18)式中所有上标“—”替换为“+”、“+” 替换为“—”得到δ-+和µ-+.

在上述非常规格点差分格式系数修正的推导中,未限制电磁参数是否为实数或复数(介质可具有增益或损耗),亦未限制其在界面两侧的跳跃量.因此对于任意电磁参数剖面的平面波导,本文描述的方法均适用.

3.3 吸收边界

波导的第一层和最后一层为开放介质层,需要做电磁波的吸收处理以降低计算区域截断带来的误差.PML 是目前计算电磁学中较为普遍采用的吸收边界条件.Berenger[19]最初通过引入非物理分裂场的方式实现PML,而利用麦克斯韦方程在复平面上的解析延拓性质,通过复坐标拖拽实现PML 的等价方式[20]在数学上更加优美且易于扩展至其他应用场景.

电磁波被有效吸收后,在第一个格点和最后一个格点外应用硬壁条件E=0 ,最终得到N×N的三对角矩阵本征值问题,利用稀疏矩阵技术可以高效地求得期望模式的有效折射率和电场分布.

3.4 高阶精度和TM 偏振

算法可以自然地扩展至高阶精度,附录给出了四阶精度的相应公式.对TE 偏振的算法做对偶变换((4)式),即得TM 偏振的相应结果.

4 算例

通过典型平面波导,如单界面等离子波导、对称波导和一维光子晶体波导的模式分析,验证算法的有效性.需要指出的是,本节算例中涉及的坐标、厚度和步长均为相应量乘以k0=2π/λ归一化后的数值.简单起见,仅考虑模式在最外层主要表现为倏逝波的情形.如图3 所示,PML 吸收边界可通过如下的实坐标拖拽实现:

图3 PML 吸收边界条件设置示意图Fig.3.Schematic diagram of the setup of PML absorption boundary conditions.

其中“±”的“+”和“—”分别对应左侧和右侧最外层,为相应的物理界面位置,εr和µr为层中电磁参数;αPML为坐标拖拽后最外侧场相对界面处场的比值,统一取为 10-8;neff,PML为待求模式有效折射率的估计值,或者为使得所有期望模式有效吸收的数值,例如取为有效折射率的最小估计值;ℜ表示求复数的实部,用于处理漏模和辐射模.算例采用通信波长 1.55 μm 处典型电磁材料的参数,如εAu=-104.2+3.7i,εair=1 ,εSi=12.25 ,εSiO2=1.96,材料的相对磁导率均取为1.

金属和介质构成的单界面表面等离子波导中,TM 模式的有效折射率可由解析式给出:

对于金属为金、介质为空气的情形,精确解为neff=1.00482710586+0.00017264861i.该波导中金属层的折射率为nAu=0.18+10.21i,其含有较大的虚部,且与空气层的折射率差异极大.三层平面对称波导中,TE 模式的有效折射率由解析的特征方程

图4 给出有效折射率的相对误差

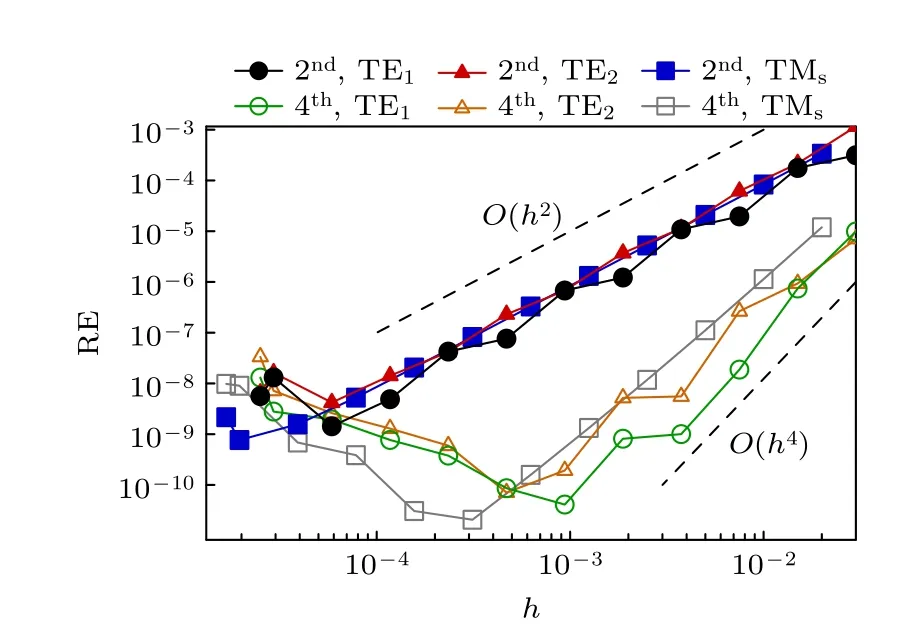
图4 收敛曲 线,单界面波导(T Ms )和 对称波导(TE1,2)模式Fig.4.Convergence curves: Modes of single interface waveguide (T Ms ) and symmetric waveguide (TE1,2).

与计算步长h的关系,其中所有材料层的归一化厚度均为 1,单界面波导的neff,PML=1.004,对称波导的neff,PML=1.05 .作为对比,图中的虚线为理想的二阶和四阶收敛曲线.可以看出,对于三个模式,二阶和四阶算法的收敛速度均与期望的阶数相符.计算误差来源包含舍入误差和截断误差.舍入误差仅与计算机硬件(本文计算在CPU 主频 3.40 GHz和双精度下执行)和计算操作次数有关,步长越小则操作次数越多,误差累积越大.对于稳定的有限差分算法,截断误差随步长减小而减小.在大步长和小步长区间,计算误差分别由截断误差和舍入误差主导.两种误差相等的步长即对应最优步长,计算误差降为极限值[22].二阶算法约在步长h=10-4时提供约为 R E=10-9的极限精度;四阶算法约在步长h=10-3时提供约为 R E=10-10的极限精度;进一步减小步长将使舍入误差超过模型截断误差.对于给定的步长,四阶方法相对二阶方法在数量级上降低误差,而计算耗时至多仅增加约(5-3)/3≈67%.例如,h=9.3750×10-4时,TE1模式在二阶方法下 R E=6.7717×10-7,计算耗时 0.181 s;在四阶方法下 R E=4.1112×10-11,计算耗时 0.244 s,计算耗时增加约 35 %.

常规有限差分法在处理界面问题时通常使用参数平滑或者平均方法.对于椭圆微分方程界面问题,不连续系数的调和平均方法比平滑方法更为精确,然而使用调和平均的有限差分法仅对满足特定条件的一维椭圆界面问题提供二阶精度[23].图5给出电磁参数未做平均处理和施加调和平均处理两种条件下,对称波导中 TE1模式和单界面波导中TMs模式的收敛曲线. TE1模式的收敛速度在两种处理下无论对于二阶还是四阶格式均降为一阶,未做平均处理时收敛曲线抖动剧烈,调和平均处理后收敛曲线趋于平稳,但误差增加约1 个数量级.对于 T Ms模式,两种处理条件下二阶和四阶格式的精度均降为零阶,且误差水平基本一致,其中调和平均处理下的收敛曲线未在图5 中给出.

图5 收敛曲线,电磁参数未做处理(-non)和施加调和平均处理(-avg)Fig.5.Convergence curves: non-averaging (-non) and harmonic averaging (-avg) for electromagnetic parameters.

图5 结果可解释如下.对于TE 模式,三点式((7)式)仅在(9)—(11)式给出的电场跳跃条件全部满足的情形下提供二阶精度收敛.在介质非磁时,电磁参数未做处理使电场及其一阶导数的跳跃条件满足,而二阶导数跳跃条件不满足,因而给出一阶收敛速度.此时,五点式((A1)式)亦仅给出一阶精度.电磁参数调和平均处理后,尽管收敛曲线的平稳性得到改善,但由于电场一阶导数的跳跃条件不再满足,致使误差上升.对于TM 模式,磁场的一阶和二阶导数的跳跃条件在电磁参数未做处理下均不满足,三点式((7)式)和五点式((A1)式)只能给出零阶精度.本文利用的IIM 方法精确匹配所需的跳跃条件,对TE 和TM 模式都能提供期望的收敛阶.

考虑更为复杂,解析方法难于处理的一维光子晶体波导.取波导堆叠为 A (LH)MC(HL)MA,其中低折射率层L 为二氧化硅,高折射率层H 为硅,芯层C 的介电常数εC=4,周围介质A 为空气.算例取M=10 ,归一化层宽wC=5,wL,H由1/4 波长堆叠条件给出:

其中h-1为小于h的临近步长.计算取wA=1,neff,PML=1.5,有效折射率的相对误差与步长的关系如图6 所示.算法对包含 23 层介质的一维光子晶体波导同样有效,四阶格式同样约在步长h=10-3时给出约为 R E=10-10的精度.

图6 收敛曲线: 一维光子晶体波导模式(TEc 为包层模式)Fig.6.Convergence curves: Modes of one-dimensional photonic crystal waveguide (TEc is cladding mode).

为了清楚地展示模场分布,令M=3 .图7 给出了3 个模式在对称轴左侧的场分布,其中取了二阶算法,步长h=1.688×10-2,其他计算参数不变.由图可见,界面处TE 模式的场及其一阶导数的连续,TM 模式的场的连续及其一阶导数的不连续,均可以被精确解析.

图7 模场分布: 一维光子晶体波导,竖直虚线标示界面位置Fig.7.Distribution of modal fields: One dimensional photonic crystal waveguide,with dashed lines indicating the positions of interfaces.

5 结论

针对平面波导的高效模式分析问题,本文基于浸入界面方法和完美匹配层吸收边界条件,提出一种具有二阶和四阶精度的全矢量计算方法.本方法只需利用取样点上折射率的值而不依赖于模场的特定函数展开形式,对于任意折射率剖面下的任意模式(导模、漏模和辐射模)均能简单而高效求解.算法不仅可进一步向高阶扩展,且其技术框架亦可应用于其他波动系统的数值模拟中界面问题和吸收边界条件的处理.

附 录

本附录罗列TE 偏振模式的四阶精度公式.对于一般的第i个格点,用五点格式

近似波动方程(6).

电场E的三阶和四阶导数的跳跃条件为

引入中间函数

将(22)式扩展为