关于区间序列的离散Opial型不等式
2023-07-13连俊勤赵大方
连俊勤,赵大方
(湖北师范大学数学与统计学院, 湖北 黄石 435002)
0 引言
1960年,波兰数学家Opial[1]给出了经典的Opial不等式:
其中,x(t)∈C1[0,h],x(0)=x(h)=0,且x(t)≥0在(0,h)上成立.经典的Opial不等式引起了华罗庚[2]等国内外众多学者的广泛关注.此后,有关Opial不等式的各种推广便出现了.其中,不仅有连续型的推广[3-4],离散化的推广[5-6],还有时标上的推广[7],以及Opial不等式在微分方程与差分方程上的广泛应用等[8-9].其中,有关离散Opial型不等式的研究可以追溯到1968年,Lasota[10]给出的离散Opial型不等式的相应证明.1995年,Agarwal和Pang[11]对各种离散的Opial型不等式进行了比较系统的分析研究,使得这些不等式的种种特征得到直观的展现.2019年,Costa等[12]研究了区间值函数的Opial型不等式,得到了一些有趣的结论,但其中一些不等式的右端系数并不是很精确.2022年,赵大方等[13]修正并进一步推广了Costa等[12]关于区间值函数的Opial型不等式的主要结论.受文献[10-13]的启发,我们继续研究了关于区间序列的离散Opial型不等式,得到了一些新的结论,并对所得主要结论给出了若干例子来予以验证.此外,文中所得结果不仅推广了经典的离散Opial型不等式,也为区间差分方程的研究提供了一些理论基础.
1 预备知识
Kc(R)是上的全体有界闭区间的集合,即Kc(),对任意的(),λ∈.其中,区间运算规定如下:

A⊖B=C⟺A=B+C.
即对∀A∈Kc(),都有A⊖A=[0,0].对于Kc()中任意两个不同的区间A,B,其H-差只有当w(A)≥w(B)时才会存在.所以,为了解决这个问题,2009年,Stefanini-Bede[15]引入了gH-差:
即gH-差对Kc()中任意A,B都成立,有
显然,(Kc(),d)是完备的度量空间,其中d为Kc()上的Hausdorff度量,即对∀A,B∈Kc(),有
此外,易知(Kc(),+,·)是拟线性空间,其中拟范数‖·‖为:
在Kc()中任取区间定义A,B间的Kulisch-Miranker偏序关系为:对于Kc()上的区间序列若对任意的指标i∈{0,1,…,N-1},都有,则称区间序列是递增的(若符号反向,则称区间序列是递减的).递增的区间序列和递减的区间序列统称为单调的区间序列.对于非退化的单调区间序列的乘法,取区间序列中{0,1,…,N}的任意指标a,b,记其所在区间为若
和
则有
成立.此外,若无特别说明,本文中出现的范数都是拟线性空间(Kc(),+,·)上的拟范数.
2 关于区间序列的离散Opial型不等式
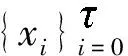
(1)
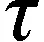
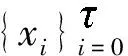
从而有
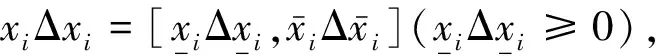
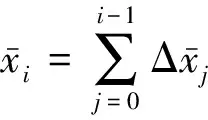

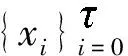
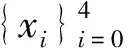
因为
显然有
成立.
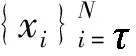
(2)
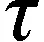
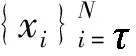
从而有



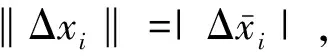
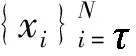
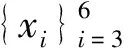
因为
显然有
成立.
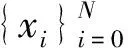
(3)
成立.其中Δxi=xi+1⊖gHxi,i=0,1,2,…,N-1,[·]是取整函数.
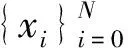
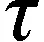
即证(3)式成立.综上所述,对于任意的N,不等式(3)皆成立,证毕.
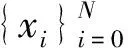
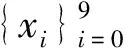

显然有
成立.
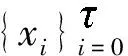
(4)
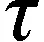
过程与定理1的证明过程类似,故省略.
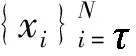
(5)
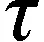
定理5的证明证明过程与定理2的证明过程类似,故省略.
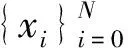
(6)
成立.其中Δxi=xi+1⊖gHxi,i=0,1,2,…,N-1,[·]是取整函数.
定理6的证明证明过程与定理3的证明过程类似,故省略.
3 结论
主要研究了关于区间序列的离散Opial型不等式,推广了几个经典的涉及向前差分算子的低阶离散Opial型不等式,为今后研究涉及向前差分算子的高阶离散Opial型不等式做了一些基础性的工作.
