安徽省合肥市肥东县城关中学(231600) 王东海

直线与圆锥曲线的位置关系问题一直是高考及各地模考的热点和难点,在这类考题的命题中往往都是探求一些特殊结论,这些结论看似特殊,实则往往都具有普遍性.我们在解答考题后要深入拓展到一般情况,还要注意探寻其它圆锥曲线的对偶性质.下面以2023 届高三武汉元月联考圆锥曲线试题的探究为例进行说明.

1 考题呈现

题目(2023 届武汉元月联考第21 题)已知椭圆C:的右焦点为F,P在椭圆C上,|PF|的最大值和最小值分别为6 和2.

(1)求椭圆C的方程.

(2)若椭圆C的左顶点为A,过点F的直线l与椭圆C交于B,D(异于点A)两点,直线AB,AD分别与直线x=8交于M,N两点,试问∠MFN是否为定值? 若是,求出该定值;若否,请说明理由.

分析这是一道涉及圆锥曲线的夹角定值问题,我们既可利用两向量的夹角公式解决,也可借助圆的性质处理,还可使用直线的参数方程来达到目的.此题对学生的数学运算、逻辑推理等核心素养的应用水平提出了较高要求,另外该题对学生思维品质的要求也较高,学生要完成正确的求解并非易事.但本题设问简洁且内容丰富,具有较大的探究空间.

2 解法探究

视角1在解析几何中遇到两直线的夹角,往往可以使用向量的夹角公式来快速处理.

解析1如图1,(1)椭圆C:.

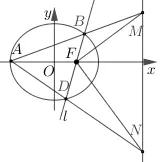
图1

(2)当直线l垂直于x轴时,l:x=2 代入椭圆方程C:3x2+4y2−48=0,解得B(2,3),D(2,−3).

直线AB方程:令x=8,得y=6,则M(8,6).同理N(8,−6).所以kFM=1,kFN=−1⇒又由题意可得直线l的斜率不为零,设B(x1,y1),D(x2,y2),直线l:x=my+2,,将其与椭圆方程联立并整理得:(3m2+4)y2+12my−36=0,则而直线AB的方程为直线AD的方程为令x=8,得因为F(2,0),所以从而

故∠MFN为定值.

视角2本题也可考虑以MN为直径的圆恒过点F,从而达到说明∠MFN为定值由圆直径式方程可得以MN为直径的圆方程为

而焦点F(2,0),再验证它是否在此圆上,因为的目的.

解析2前同解析1,可得

从而∠MFN为定值.

评注这里利用了圆的直径式方程,可以较快地写出以MN为直径的圆的方程,节约了时间.

视角3考虑到直线l经过焦点F(2,0),故这里也可利用直线的参数方程来解决该题.

解析3因直线l经过焦点F(2,0),故设直线l的参数方程为将其代入椭圆方程C:3x2+4y2−48=0,可得:3cos2θ+4sin2θ)t2+12 cosθ·t−36=0,则

又因B(2+tBcosθ,tBsinθ),D(2+tDcosθ,tDsinθ),从而直线AB方程为:令x=8,得同理可得从而

故∠MFN为定值

视角4本题还可尝试采用定比点差法来解决,这种解法往往别具一格.

解析4不妨设且直线DB上必存在点Q,使又设D(x1,y1),B(x2,y2),则由定比分点坐标公式得

因D,B在C上,故

上述两式相减得:

3 结论一般性推广

由上面的分析和解答,∠MFN为定值,那么此结果是偶然还是必然呢? 在考题中,a,b均为特殊数值,如果将参数a,b一般化,焦点F(2,0)及其对应的准线x=8 也变为一般的F(c,0)和会得到什么结果呢? 焦点或准线再一般化呢? 基于以上思考,可得以下几个一般性结论:

结论1一般地,已知椭圆C:的左顶点为A,x轴上一定点S(s,0),过点S的直线l与椭圆C交于B、D(异于点A)两点,直线AB,AD分别与直线x=t交于M、N两点,则kSM· kSN必为定值.

证明由题意可得直线l斜率不为零,设B(x1,y1),D(x2,y2),直线l:x=my+s,,将其与椭圆方程b2x2+a2y2−a2b2=0 联立得到(b2m2+a2)y2+2mb2sy+b2(s2−a2)=0.从而,

推论1已知椭圆C:的右焦点和左顶点为F,A,过点F的直线l与椭圆C交于B,D(异于点A)两点,直线AB,AD分别与准线交于M,N两点,则∠MFN必为定值.

推论2已知椭圆C:的左顶点为A,x轴上一定点S(s,0),过点S的直线l与椭圆C交于B、D(异于点A)两点,直线AB,AD分别与点S对应的极线交于M,N两点,则kSM·kSN为定值.

在结论1 中,取s=c,则有

推论3椭圆C:的右焦点和左顶点为F,A,过点F的直线l与椭圆C交于B,D(异于点A)两点,直线AB,AD分别与直线x=t交于M,N两点,则kFM·kFN为定值.

4 类比推广

我们还可尝试把结论类比到双曲线和抛物线.

结论2一般地,已知双曲线C:0)的左顶点为A,x轴上一定点S(s,0),过点S的直线l与双曲线C交于B、D(异于点A)两点,直线AB,AD分别与点S对应的极线交于M、N两点,则kSM·kSN为定值.

结论2 中令s=c,则恰有kSM·kSN=−1,即有

推论4如图2,已知双曲线C:0)的右焦点和左顶点为F、A,过点F的直线l与C交于B、D(异于点A)两点,直线AB,AD分别与准线交于M、N两点,则∠MFN为定值.

图2

结论3一般地,已知抛物线C:y2=2px(p>0)的顶点为O,x轴上一定点S(s,0),过点S的直线l与抛物线C交于B、D(异于点A)两点,直线OB,OD分别与点S对应的极线x=−s交于M、N两点,则kSM·kSN必为定值.

在结论3 中,令s=p/2,则也恰有kSM·kSN=−1,即有

推论5如图3,已知抛物线C:y2=2px(p>0)的焦点和顶点为F,O,过点F的直线l与抛物线C交于B、D(异于点O)两点,直线OB,OD分别与准线交于M、N两点,则∠MFN必为定值.

图3