广东省中山市中山纪念中学(528454) 李文东

解三角形中的最值与取值范围问题,在高考中考查形式灵活,是教学中的难点,常常在知识的交汇点处命题,与函数、几何、不等式等知识结合在一起.我们知道三角形只要满足三个条件,那么这个三角形就基本唯一确定了,而少于三个条件时,其边、角、周长和面积就可以变化,从而就有了求这些量的取值范围问题.这类问题的求解方法主要是充分运用三角形的正余弦定理,结合不等式或函数的知识,必要时运用轨迹的思想,本文针对一道三角形面积的最值问题谈谈对此类问题的一些思考.

一、试题及其解法分析

题目(2023 届华大联盟10月高三联考数学试题的第16 题)在∆ABC中,AC⊥BC,AC=BC,E为线段AC上一点(不与A,C重合),D为BE延长线上一点,AD=2,CD=1,则∆ABD面积的最大值是____.

该试题内涵丰富,从知识层面看,主要考查平面图形的几何性质、解三角形(正余弦定理)、以及动态图形中的三角形面积的最值等知识;从能力层面看主要考査运算求解、逻辑推理等方面的能力,突出考查数学运算、逻辑推理等核心素养;试题的思维过程和运算过程体现了能力立意的命题思想,较好地体现了对平面几何中的解三角形、几何图形的性质等核心内容和转化与化归、函数思想,数形结合等基本思想方法的考查,是一道具有教学价值的好题.

下面笔者从不同的角度对该题给出解析.

解法1(几何法)显然∠ADC为钝角,如图1,过点B作BF⊥AD于点F,过点C作CG⊥BF于点G,过点C作CH⊥AD于点H,由于AC⊥BC,故∠CBG=∠ACG=∠CAD,AC=BC,故Rt∆BGCRt∆AHC,故BG=AH,于是BF=BG+GF=AH+CH=AD+DH+HC=2+DH+HC,而DH2+HC2=CD2=1.由基本不等式得故当且仅当DH=HC时等号成立;从而.

图1

解法2(轨迹思想)建立如图2世纪的坐标系,则A(2,0),设C(x0,y0),由于CD=1,故设B(x,y),∆ACB为等腰直角三角形,为了方便的得到点B,C的坐标关系,我们采用复数进行旋转变换的方法,显然得,代入,化简得点B的轨迹方程为:x2+(y−2)2=2,显然

图2

解法3(函数思想)设AC=x,∠CAD=α,∠ACD=β,则在∆ACD中,由余弦定理得.所以所以∆ABD的面积

令f′(x)>0,得令f′(x)<0,得所以f(x)在上单调递增,在上单调递减,所以

即

解法4(三角函数)设∠ADC=θ,在∆ACD中,利用余弦定理可得:AC2=AD2+CD2−2AD·CDcosθ=5−4 cosθ,在∆ACD中,利用正弦定理可得:,得于是cos ∠DAC=而∆ABD的面积

解法5(广义托勒密定理)先介绍广义托勒密定理:

在凸四边形ABCD中,有AC·BD≤AB·CD+AD·BC,等号当且仅当A,B,C,D四点共圆时成立.其证明可参考文献[1].

设AC=BC=x,则由广义托勒密定理AC·BD≤AB·CD+AD·BC得:于等号当且仅当A,B,C,D四点共圆时成立,上述等号成立的条件是∠ADB=90◦和A,B,C,D四点共圆,由∠ACB=90◦和A,B,C,D四点共圆知∠ACB=∠ADB=90◦,上述两等号恰好同时成立,于是是而.

点评上述五种解法分别从不同的角度切入,解法1 主要是利用平面几何的知识与基本不等式,对平面几何能力要求较高;解法2 根据题中条件,建立恰当的坐标系利用复数的旋转得到点B的轨迹方程,由于新版教材已经有复数的三角形式,因此对于复数的旋转学生不难理解,求解显得十分简洁,而且该方法便于推广;解法3 则是引入AC=x,然后将∆ABD的面积表示为x的函数,转化为函数求最值问题,推导和运算都很复杂;解法4 是引入∠ADC=θ作为参数,然后利用正余弦定理将∆ABD的面积表示为θ的三角函数,想法和解法3 类似,但是计算要简单很多;解法5 最简捷,但是需要用到广义托勒密定理,而且局限性很大!

二、利用轨迹求解三角形最值问题举例

对于三角形中的某些最值和范围问题,若是我们能够从轨迹的角度去思考,往往能够起到降低思维,减少运算的效果,下面举例说明.

例2(2011年高考新课标卷理科第16 题)在∆ABC中,B=60◦,则AB+2BC的最大值为____.

分析本次常见的解法是利用正弦定理边化角转为三角函数或者利用余弦定理结合不等式知识求解,其实利用轨迹思想有下面更直观的解法.

解在∆ABC中利用正弦定理得:2R1,其中R1为∆ABC外接圆的半径,如图3,延长AB至D,使得BD=2BC,则AB+2BC=AD.在∆ACD中,∠CBD=120◦,设∠D=θ,由正弦定理得化简得联立sin2θ+cos2θ=1,可得于是其中R2为∆ACD外接圆的半径,显然AB+2BC=AD的最大值为∆ACD外接圆的直径,即为.

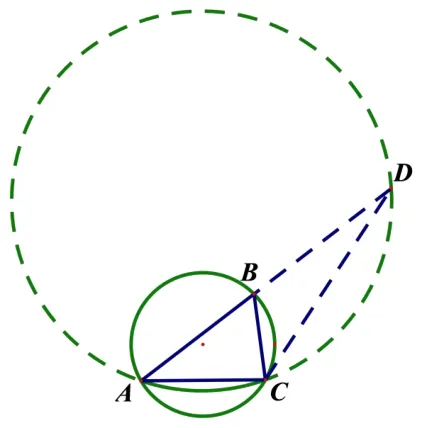
图3

例3在∆ABC中,AD为∠BAC的平分线,且BD=2DC,BC=6,求∆ABC面积的最大值.

解因为AD为∠BAC的平分线,由角平分线定理得以B为原点,BC所在直线为x轴,建立直角坐标系,则B(6,0),设A(x,y),于是有此即为点A的轨迹方程.于是即∆ABC面积的最大值为12.

点评本题中点A的轨迹的背景是阿波罗尼斯圆:设点A,B为两定点,动点P满足|PA|=λ|PB|,当λ >0 且1 时,动点P的轨迹为阿波罗尼斯圆.

除了三角形中的动态问题可以考虑用轨迹方法求解,其实对于一些确定性问题也可以利用轨迹思想求解,往往能够起到意想不到的效果.

例4在∆ABC中,角A,B,C所对的边分别为a,b,c,且2acosB=2c−b.

(1)求A;

(2)若∆ABC内一点P满足:PB⊥PC,∠APC=120◦,且AC=3AB=3,求tan ∠ACP.

解(1)由正弦定理及2acosB=2c−b,得2 sinAcosB=2 sinC−sinB,又A+B+C=180◦,所以sinC=sin(A+B),故2 sinAcosB=2 sin(A+B)−sinB=2 sinAcosB+2 cosAsinB−sinB,即2 cosAsinB−sinB=0.又因为sin0,所以又A∈(0◦,180◦),解得A=60◦.

(2)如图4,以C为原点,AC所在直线为x轴,建立直角坐标系.由题意A(3,0),由∠BPC=90◦知点P在以BC为直径的圆上,其方程为:由AC=3和∠APC=120◦,根据正弦定理知点P在以AC为弦且半径为的圆上,不难求得其方程为:两圆方程相减得直线PC得方程为:由题意其斜率即为tan ∠ACP的值,故.

图4

三、拓展练习

作为上述思想和方法的应用,读者可以尝试解决以下问题:

1.在平面四边形ABCD中,AB=1,BC=2,∆ACD为等边三角形,求∆BCD面积的最大值.(答案:

2.在平面四边形ABCD中,AB=1,∆ACD为等腰直角三角形,,求BD的最大值.(答案:

3.(2013年高考全国I卷理科第17 题)如图5,在∆ABC中,∠ABC=90◦,BC=1,P为∆ABC内一点,∠BPC=90◦.

图5