■江苏省沙溪高级中学 邵敏亚 魏志英

圆锥曲线离心率问题,历来是各级各类考试的命题重点,由于这类问题方法灵活,综合性较强,因而也是同学们学习的难点。那么这类问题该如何破解呢? 同学们或许能从下面几个例题的“一题多解”中得到启示。

一、求离心率的值

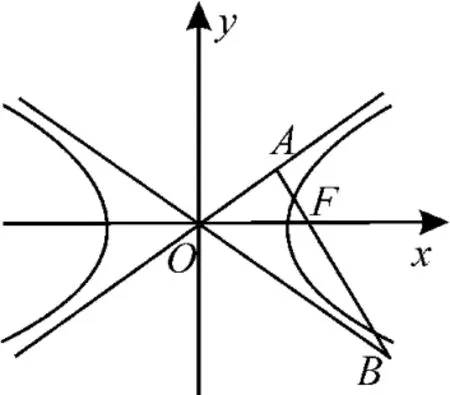
图1

(法4)如图2,过点F向双曲线的另一条渐近线作垂线,垂足为D,则|DF|=b,|BF|=2b。

图2

法3首先将∠AOF与∠AOB的正切值用a,b表示,再利用正切二倍角公式得到a,b之间的关系式,进而求出离心率的值。此法利用了双曲线焦点到渐近线的距离为b的特征,结合图形,巧妙地利用了长度关系及双曲线的对称性。解题过程中体现了数形结合思想与方程思想,对大家的观察能力及分析问题的能力有较高的要求。

法4 则通过添加辅助线,将“|AF|与|BF|”化到同一个直角三角形中,利用|AF|与|BF|的长度关系及相似、双曲线渐近线的对称性得到∠AOF的大小,进而求出离心率,构思巧妙,易于运算。本法与法3 类似,但优于法3,体现了数形结合思想的妙用。

二、求离心率的取值范围

图3

点评:求圆锥曲线离心率的取值方法一般采用不等式法和函数值域法。

法1利用椭圆的对称性,将|BF|转化为|AF′|,将|AF|与|AF′|用角θ表示,再利用椭圆的定义将离心率e表示为θ的函数,将离心率e的取值范围问题转化为三角函数的值域问题,求解时应特别注意角θ的取值范围。本法体现了函数思想的应用。

法2将点A的坐标用角θ表示,然后代入椭圆方程解出cos22θ。利用求出cos22θ的取值范围,得到关于e2的不等式,结合0＜e＜1 得出e的取值范围。法2利用了点在曲线上,即点的坐标满足曲线方程的特征,解题过程中体现了方程思想与化归思想,对大家的运算能力及化归能力有较高的要求,而利用余弦函数的有界性将问题转化为不等式问题是解题的关键。

法3将m,n用θ表示,利用椭圆的定义及△AFF′是直角三角形,将e表示为tanθ的函数,利用对勾函数求解。本解法与法1类似,只是对的处理上有所不同。这里利用化切处理再结合均值不等式得解,体现了函数思想与化归思想,在数和式的处理上对我们提出了较高的要求。

法4则利用极端情况,即∠AOx=时的情况,将|OA|2的长度用a,b表示,再结合|OA0|≤|OA|=c得到事实上这里也可用余弦定理及勾股定理将|AF|,|AF′|用c表示,再结合椭圆定义得解。法4采用“以静制动”的方式处理问题,要求同学们具有较好的观察能力与推理能力。

法5利用S△AFB=S△AFF′,结合焦点三角形面积公式将表示,再利用sin 2θ的有界性求出e的取值范围。本解法与法2类似,利用了正弦函数的有界性,同样要求大家具有较好的分析、解决问题的能力和丰富的函数不等式的知识储备。

三、离心率之间的关系

例3已知椭圆C1与双曲线C2有相同的焦点F1,F2,曲线C1,C2的一个交点为P,且PF1⊥PF2,则椭圆C1的离心率e1与双曲线C2的离心率e2一定满足的关系是( )。

图4

点评:本例是个选择题,求解时不仅要用到圆锥曲线的有关定义和几何图形的特征,还可采用特殊化法。从而达到快速解答的目的。

本例法1取特例,对选项进行检验排除,可以快速地得到答案。作为选择题,如果能用特例进行排除,可以提高准确率。本解法体现了特殊化方法的优势。

法2 是求解圆锥曲线离心率的常用方法,利用圆锥曲线定义结合平面几何知识,从几何关系寻求a,c的关系式。分析图形的几何特征,利用几何关系建立关于a,b,c的方程是解决离心率问题的常见策略。法2体现了方程思想的运用,对代数式的恒等变形能力要求较高。

法3利用椭圆与双曲线焦点三角形的面积公式,得到曲线之间的关系。椭圆焦点三角形面积(其中θ=∠F1PF2),法3体现了方程思想与化归思想的运用,要求我们具有较好的分析、解决问题的能力。

法4最为简捷,但要求我们善于运用代数式的恒等变形,具有较高的数学运算素养。