朱 婉(江苏省徐州市贾汪中学 221011)

在开展高中数学实际解题教学的过程中,教师常常会发现,有部分学生并没有积极参与到学习中。这会导致这部分学生无法与其他学生进行充分的讨论与交流,很难有所收获。陶行知先生在《民主教育》一文中指出:“民主教育是教人做主人,做自己的主人,做国家的主人,做世界的主人。”为了激发学生的主观能动性,教师应该在高中数学解题教学中积极融入陶行知先生的民主教学思想,优化教学活动。

一、 引导不同层次的学生探索知识

由于学生的学习、理解以及探索水平存在一定的差异,最终得到的学习效果必然会有所不同。面对这种情况,教师不仅要始终保持积极的态度,鼓励学生,让学生尽自己所能参与教学活动,还要为学生量身定制相应的练习,引导他们展开探索。以下面这道问题为例。

例1:已知复数(x2-1)+(y+1)i大于复数(2x+3)+(y2-1)i(x,y∈R),试求x,y的取值。

针对学困生,教师可以提出这样的问题:如果从复数这个概念着手,要满足怎样的条件,才能对两者进行大小比较? 学困生虽然缺乏解题经验,但是在教师的细心引导下,他们依然能够学习到数学中的基础知识,并且从中受到相应的启发。于是,学困生得到答案:只有这两个复数的虚部都为0,它们才能正常比较大小。

教师引导学中生解题时,要让他们有机会展现自己的运算能力。学中生的解题方法如下:因为(x2-1)+(y+1)i＞(2x+3)+(y2-1)i,那么可得x2-1＞2x+3(式1),y+1=0(式2),y2-1=0(式3),综合以上三式可得x＜1-或x＞1+,y=-1。这种解题思路有值得学困生学习的地方。

针对学优生,教师则应将教学的重点放在以多种方式解决问题上。比如,有的学优生会应用数形结合的方式来解决这一问题:将复数(x2-1)+(y+1)i(x,y∈R)与(2x+3)+(y2-1)i(x,y∈R)呈现在坐标上,然后应用构建复数形方法构建几何图形来求x,y的取值。

二、 引导学生掌握科学的学习方法

有的学生没有掌握解决问题的方法,于是就产生了“自己解决不了问题,就先等教师或者其他同学解题,最后再参考他们的解题方法”的错误思想,这种思想的存在,会在一定程度上阻碍他们知识的消化和吸收。教师需要融合陶行知先生教学思想,帮助学生掌握“以问题为导向”的学习方法。以下题为例。

教师提问:(1)这一题涉及哪些知识点? 学生在结合问题的解题需求以及自己的学习经验之后,能够发现“如果函数的表达式为f(x)=x,那么f(x)的取值范围就是函数f(x)的值域”。于是,学生意识到解题第一步就是要关联具象化的问题和抽象化的理论,让理论成为解题的指导。

(2)函数值域求法有几种? 结合每种求法的特点,这一题适于应用什么方法? 在这两个问题的引导下,学生提出“观察法、配方法、换元法、反函数法”这四种求函数值域的方法,并且发现这一题并不适合采用配方法和反函数法来解决。配方法适用于把函数转换成为二次函数的复合函数形式,这一题难以完成这种转换。而且这一题的自变量式子原本就比较复杂,求反函数会让问题变得更复杂。那么,如果采用观察法呢? 同样不行,式子过于复杂,难以直接求出函数的值域。排除了以上三种方法之后,学生只好将函数式子化简,按照配方法的思路,将自变量式子的分母分解为（1+x2）2,同理,将分子分解为x（1-x2）,通过等量变换,学生最终得到了这样的式子。

通过学习,学生掌握“从问题本身出发,以理论作为指导,找出解题方法,然后根据式子特征找到最佳解题方法”的解题思路。

(3)本题解题难点究竟在哪里? 学生认为,如果直接分析函数的值域,解题过程就会变得十分烦琐。于是,在教师的引导下,学生会将思考的角度放在“能否应用数学思想来完成解题”上。得到教师的启示后,学生发现本题中,自变量的式子与三角函数中的万能公式十分接近。依此思路,学生会令,将函数变为三角函数,得。

(4)结合整合的式子,如何运算和求解? 学生结合所学“求取三角函数值域”的知识得:y∈。

在完成了本题的练习之后,学生便掌握“发现数学问题,到关联解题理论依据”“列举解题的基本方法,结合实际问题进行有效选择”“找出问题的重点难点,应用数学思想来对问题进行转换,结合新问题的条件,解决原有问题”这三种巧妙的解题技巧。

三、 引导学生参与有趣的学习活动

有的学生认为解题的过程太枯燥,难以沉下心来专心解题。因此,教师可以开展趣味化学习活动,让学生能够在良好的学习氛围中愉快地开展解题学习。

比如,教师可以引导学生以角色扮演的方式呈现出自己完成的一道经典习题(这一题需要呈现出一种解题思想)。

例3:已知锐角α,β,γ满足cos2α+cos2β+cos2γ=1,求证:。

让一名学中生来解题,学中生采用三角方法来进行求解,但是发现计算过程变得十分烦琐。此时,教师可以引导学中生观看这一式子的特征。而根据已知条件和未知答案,学中生会发现例3 中已知条件的式子与立体几何中长方体对角线的性质公式有些相似。此时,学生可以模仿教师的解题思想,画出一个长方体的图像(如图1所示),应用数形结合的思想进行解题。在图1 中设长方体ABCDA1B1C1D1的长、宽、高分别为a,b,c,令它的对角线AC1与棱AB,AD,AA1的夹角分别为α,β,γ,那么可知cos2α+cos2β+cos2γ=1,并且可 以 得 到,那么可得。

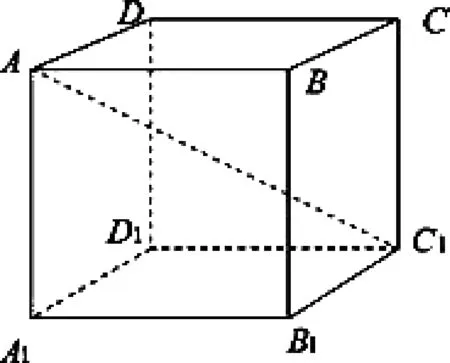
图1

学生最终得到“当且仅当a=b=c时取等号,即α=β=γ时结论成立”的结果。

学生在完成习题的讲解后,还要分享自己的解题感受。实际上,并非习题没有给出必要条件,而是学生在处理文字信息时,难以很快察觉到习题中存在这种已知条件。如果把抽象的文字信息反映在数学图形上,就能够很快在图形中找出对应的数量关系。