陈凯 上海市位育中学

《孙子兵法》的兵势篇中这样写道：激水之疾，至于漂石者，势也；鸷鸟之疾，至于毁折者，节也。故善战者，其势险，其节短。势如彍弩，节如发机。在古文中，“机”字的含义之一，是用于释放箭的组件，其中很重要的零件就是扳机（古称扳机为悬刀），《尚书·太甲》中说：“若虞机张，往省括于度则释”，就是说要在合适的时机扣动扳机放箭。在使用一般的弓箭时，在把弓拉开的过程中以及在拉开弓之后直到释放箭之前，手臂需要承担很大的负荷。而具有待发装置的弩就不一样，在拉弓到位后，承担负荷的是弩臂。在扣动扳机时，射手只需要施加一个小的力量，然后借助机关将之前积蓄的巨大的能量瞬间释放出来。

弓弩的作用不只是杀伤敌人，古人也利用射出的火箭或射出能发出声响的鸣镝来传递信息。不过就算弓弩射出箭的距离很远，由于受地球引力和空气摩擦力的影响，箭总是要落回到地面上。这里有一个夸张但合理的假设，如果发射的方向和力度都足够精准，射出的箭恰巧击中远处弩的扳机，那么就能触发远处的弩也射出箭，理论上说，只要后续接力的弩足够多，触发的过程就可以一直继续下去。可以将这个过程中的某些关键要素抽取出来，如拉满弓所积蓄的势能、用以释放能量的机关的触发、机关触发后的连锁反应等，本文将要说明，这些要素不仅和信息的传输有关，还与计算有关。

● 用戈德堡机械装置传输信息

这样一组（理想状态下）能够实施接续触发动作的弓弩，其行为在某些地方类似于戈德堡机械装置。戈德堡机械一词来源于艺术家鲁布·戈德堡的系列漫画，在漫画中，某个复杂的机械系统由形态各异的简单机械机构组合而成，初始触发动作经由一系列机关逐级传递下去，直至驱动最终的机械结构完成某项任务——通常是打鸡蛋、挤果汁、敲闹铃之类的任务，其简单程度与整个系统的复杂极不相称，图1显示的是艺术家所想象的众多戈德堡机械装置中的一种。在网络上有许多构思奇妙的戈德堡机械装置的视频，在浏览了各种有趣的设计后，很容易联想到，可以借助某些戈德堡机械中的传动机构，来改进连锁击发的弓弩装置，使得即便在箭的落点不甚精准的情况下也能借助机械传动扣动下一级弩的扳机，提高信息传输的成功率。

图1 1932年鲁布·戈德堡创作的漫画《橘子榨汁机》

与借助各种各样奇怪的机关来实现动作传递的戈德堡机械装置不同的是，（理想状态下）在箭射时弓弩扳机所引发的连锁反应中，每个触发行为都是一致的，这个行为可以被一模一样复制到n组释放箭和被触发的装置中。同时也可以看到，弓弩连锁击发模型与戈德堡机械装置有相似之处，就是两者都是通过机关的触动，将积蓄的势能释放出来。很自然可以联想到：用一个戈德堡机械装置来实现信息的传输，是完全有可能的。下页图2展示了一个相当简单的可以接续传递信息的戈德堡机械装置的例子：从斜面上滚下的小球推动杠杆，使得杠杆顶部的小球掉落，接下来就是不断重复刚才的过程。这个设计模型可以在Algodoo物理沙盘中运行，在制作这个模型时，只有第一个触发装置的搭建耗费了一些时间，而后续触发装置只要经由复制粘贴就可以快速放置到位，通过这个制作可以充分体会到模块化对提高工作效率的作用。

图2 一个可以接续传递信息的戈德堡机械装置

无论是弓弩连锁击发模型还是小球连锁碰落模型，在用于传输信息时，都有相同的弱点。其一，它们都只能一次性发挥作用，需要在每次使用后，重新将弓拉满，或将小球放置到杠杆顶端；其二，它们都无法改变所传递信息的状态，举例说，箭的射出总是导致后续箭的射出，而不会导致后续箭的停发，而停发的箭也不会使后续箭自动射出。想象一下，若是某弓弩在没有被其他箭射中扳机的情况下自动射出箭，那该是多么匪夷所思的事情。

这样一个用连锁击发或碰落装置组成的系统，无论中间接续了多少级，整个系统的输出状态和输入状态都是锚定的。那么，这个系统虽然确实能够传输信息，但因为其机械结构不能对信号取反，计算功能是受到很大限制的。

● 机械装置的数学模型与问题

可以想象改造上述连锁击发装置，使其能根据多个输入来决定输出。例如，某弓弩有两个扳机，只有当两个扳机都被击中时，箭才会被射出。为了研究这种弓弩的行为，可以试着将其抽象为数学模型，用函数X(a,b)代表弓弩的行为，函数返回结果1表示弓弩射出箭，结果0表示未射出箭；而函数内的两个参数a和b是两个扳机的状态，被击中为数字1，未被击中为数字0。显然，X(1,1)返回的值为1，而X(1,0)、X(0,1)和X(0,0)返回的值都是0。当然，若不使用弓弩，也可以用小球来实现类似的装置。

以上过程是试图建立逻辑上“与”运算的函数，但仔细分析后可发现，X(a,b)函数所抽象的弓弩的行为，和逻辑“与”运算是有区别的。其一，参数a和b的值不是同时改变的，设想一下，当对准下一级弓弩的两个扳机射出两杆箭时，物理上很难做到同时击中扳机，这样，两个参数中总是其中一个由0变1，继而另一个参数再由0变为1；其二，装置的运作不仅与作为输入的箭有关，还与事先有没有张满弓的能量积蓄有关；其三，当参数a和b的值有一个或两个都是0的时候，其含义是不明确的，因为分不清楚到底是因为前一级弓弩没有射出箭而输入0，还是因为前一级弓弩根本就没有工作而输入0。这种不知0为何物的微妙的感觉，让人想起王维的《鸟鸣涧》诗句“人闲桂花落，夜静春山空”中的“空”，而一旦后一级装置接收到前一级装置传来的信号，则又颇有“月出惊山鸟，时鸣春涧中”的意味。诗句中的“空”是由“时鸣”衬托出来的，而“空”却不是“时鸣”的反面。从科学实验的角度看，用以表述弓弩的行为的X(a,b)函数之所以与现实不符，是因为没有也难以将时间作为实验的因变量，X(a,b)函数仅能返回一个本征值。从电子电路的角度看，弓弩触发是一个脉冲信号，这个信号在没有被展宽时是不适用于逻辑函数的。

扩展思考一下，如果想要用弓弩实现逻辑上的“异或”运算，那就更不可能了，“异或”运算的要求是，在两个输入不一致的情况下，输出为1，对应到弓弩的行为上，就是只有在一个扳机被击中，另一个扳机未被击中的情况下，才引发后续的释箭动作，但当两个扳机都被击发或都没有被击发时，这样情况下就不引发后续的释箭动作。正如前面所说，因为不能保证射出的箭在时间上绝对同步到达扳机，一个扳机被击中后箭已离弦，即便另一个扳机再被击中，箭也不可能自动收回，所以这样的装置是几无可能制作出来的。由于无法实施“异或”运算，这个弓弩连锁击发模型无法实现哪怕最简单的二进制的1加1的运算，因为两个二进制数码1的相加，其低位必然是0。之所以要花费篇幅来讲此类装置做不到什么，其用意自然是想让大家去思考，怎样才能解决这些装置做不到的问题。

● 计算装置中的信号取反

英国物理学家大卫·多伊奇（David Deutsch）说：“每一个算法都是由物理系统执行的，即便是具有纸笔的数学家，算盘等机械系统还是现代计算机。”当今人们每天使用的各种数码设备无疑都能进行计算，只要相信所有的计算过程是不可能脱离物理实体而凭空存在着的，就能推理获知，计算过程必然对应着某种机械过程。《孙子兵法》中说“势如彍弩，节如发机”，但前文中用“机”计算的尝试，还存在着很多问题，如只能一次性传输信息、不能实现信息的取反、难以处理同步的信息输入等。有一个词语叫“神机妙算”，相信这个世界上存在着某种“机”来对应着某种“算”。

《墨子·公输》中说：子墨子解带为城，以牒为械，公输盘九设攻城之机变，子墨子九距之。公输盘就是鲁班，他和墨子开展了一场攻城战的演习，使用的是木质的机械模型。鲁班将攻城的机械模型改变了很多次，但每次都被守城方的墨子破解。这次演习的结果是，使得楚王打消了攻打宋国的意图。从这个故事中可以得到的一个启发，就是可以借助模型推演来预测结果。

借助模型可知，制作能够实现对输入信号取反的装置是可能的。模型的实现方法可能是多种多样的，不过要使其尽可能结构简单、运行过程明显，倒也不是件容易的事。图3所展示的机械装置的工作原理是这样的：用左上角斜坡滚落的一系列的球作为输入信号。当有球连续不断滚入槽内时，代表信号1；当没有球连续滚入槽内时，代表信号0。而右下角斜坡滚落的一系列球作为输出信号，其行为和代表数值与输入类似。装置的关键在于一个跷跷板结构，当输入信号为1时，也就是说，当有球连续不断砸到跷跷板左侧时，输出端的球无路可去，则右下角没有球滚落，表示输出为0。而当输入信号为0时，也就是说，跷跷板可以自由晃动，这样右侧的球就可以从右下角斜坡滚落，表示输出为1。由于这个装置是否能取反，取决于右上角管道是否有球滚入，所以此装置事实上是一个受控非门。这个装置还实现了一个重要的功能，就是只要右上角的管道能源源不断地提供小球，装置就能够重复实现信息的输入和输出的计算。

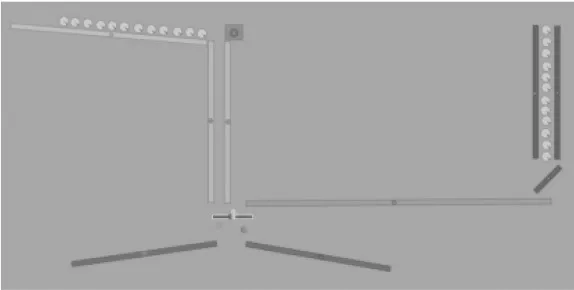
图3 对输入信号取反的机械结构

《老子》中说“安以动之徐生”，可是为什么呢？周敦颐的《太极图说》似乎给出了解释：“动而生阳，动极而静，静而生阴，静极复动。一动一静，互为其根。分阴分阳，两仪立焉。”周敦颐将原因归于动静互为其根，这种把问题引向另一个缘由的形而上解释，还是很难让人真正领会“动转静”与“静转动”的真谛。笔者搭建的这个对输入信号去取反的机械结构，却能将“由激发而抑制，由抑制而激发”的过程很直观地呈现了出来。

若是将两个取反机构级联，如图4所示，则输入和输出可呈现更复杂的关系。

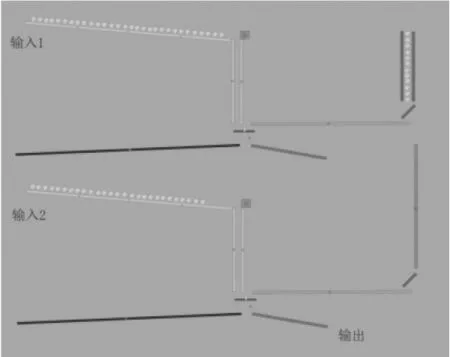
图4 将两个取反机构级联

经实验，或单纯用逻辑推理可知，当输入1和输入2时信息均为0，也就是说在没有小球在输入端滚入的情况下，输出信息为1。其他情况，输出信息都是0。理论上说，可以将更多的取反机构级联在一起，但小球滚落速度的差异，会对系统的稳定运行造成很大的麻烦。大家或许会想，用什么形式的信号来代替小球滚动，才能避免小球滚落速度不同所产生的影响。答案可能是电，或是光，或是其他什么人们当前还不知道的物质或现象。

● 取反机构的数学模型

很容易用数学函数X(a,b)来描述取反机构的行为，它应当有两个输入参数：其一，a对应触动的机关，也就是孙子所说的节或机；其二，b对应积蓄的能量，也就是孙子所说的势或弩。函数的输入和输出行为是这样的：

X(0,无) --> 0

X(0,有) --> 1

X(1,无) --> 0

X(1,有) --> 0

函数的第二个参数的值不参与运算，只是决定支撑计算装置运行的能量是否有效，所以用“有”和“无”来表示，对于图3中的取反机构，假设积蓄能量的参数总是“有”，则：

X(0,有) --> 1

X(1,有) --> 0

显然，这个装置的行为等同于逻辑上的“非”运算。可以看出，只要能量端总是“有”，X(a,b)就可能返回两个本征值中的一个值。

对于图4中的级联的取反机构，其对应的函数是X(a,t(X(a,b)))，函数中调用了函数自身，这便是一种递归，也就是说，哪怕是最简单的逻辑函数，在其真正的物理实现过程中就已含有递归了。X(a,t(X(a,b)))中的X(a,b)对应的是第一级取反机构的行为，t的作用是将其运算结果转化为第二级取反机构的能量，t(1)返回的是“有”，而t(0)返回的是“无”，这个结果结合第二级取反机构的输入再一次进行运算。函数的输入和输出行为是这样的：

X(0,t(X(0,有))) --> X(0,t(1))--> X(0,有) --> 1

X(0,t(X(1,有))) --> X(0,t(0))--> X(0,无) --> 0

X(1,t(X(0,有))) --> X(1,t(1))--> X(1,有) --> 0

X(1,t(X(1,有))) --> X(1,t(0))--> X(0,无) --> 0

在该函数中，第一级取反机构的能量总是“有”，而后续级联机构的能量，则经由运算而获得，所以对于装置的使用者来说，可以进一步简化函数的形式为NOR(a,b)，其输入和输出行为是这样的：

NOR(0,0) --> 1

NOR(0,1) --> 0

NOR(1,0) --> 0

NOR(1,1) --> 0

对数字逻辑比较熟悉的读者能立刻看出，这其实就是逻辑中的或非门，或非门是一种通用逻辑门，利用或非门可以演化出其他所有种类的逻辑门（真实电路中最常见的是用两个三极管组成与非门实现通用逻辑），当然，也能借助或非门实现前文中所说的难以实现的异或逻辑运算。逻辑运算是一种数学上的抽象，但对应逻辑运算抽象行为的物理实体并不是自然而然就存在着的，而是依靠一系列精巧的动作转换和能量传递来实现的。人们可以构建模型来验证自动化装置的数学计算的可行性，较之公输盘构建攻城机械模型更进一步的是，人们还可以用数学的模型代替实体的模型，来研究这个实体模型的行为。构建数学模型来解决现实问题是一回事，构建数学模型来研究数学计算行为本身，则又是另一回事。在人类历史上，数学模型的出现常先于可实现此模型行为的实体的出现，在乔治·布尔提出布尔逻辑近百年之后，才有香农的《对继电器和开关电路中的符号分析》一文问世。纵观布尔逻辑的提出直到用继电器实现各种布尔逻辑运算的历程，就可以感受到具有计算思维特征的抽象是如何从数学思维中浮现出来的。