付为刚， 廖 喆， 熊焕杰， 马骏驰

(中国民用航空飞行学院 航空工程学院， 四川 广汉 618307)

0 引言

板壳结构在航空航天[1,2]、武器装备[3,4]以及包装制品[5]等领域应用广泛.板壳结构在受到的压缩载荷达到临界值时会发生屈曲失稳破坏，从而造成灾难性的事故.作为影响结构安全性的重要设计因素，板壳结构的屈曲失稳特性一直是人们关注的热点.

近年来，许多学者对含简支与固支边界条件下矩形板的屈曲失稳特性进行了深入研究[6,7].Wang等[8]采用辛叠加方法得出了四种简支与固支组合边界条件下的解析解，其结果可作为其它数值方法的基准.Salama[9]采用Raylei-Ritz法研究了端部和中部承受单向轴压作用下加载边简支、非加载边固支矩形板的屈曲失稳特性.该方法依赖于事先假定满足边界条件的挠度函数.葛威延等[10]采用高阶有限条传递矩阵法，分析了两对边简支、两对边固支边界条件下四边受压矩形板的屈曲失稳问题，研究结果表明，该方法在有限条传递矩阵法的基础上进一步提高了计算精度.然而，在复杂的工程应用环境中，矩形板四边也存在含自由边界条件的现象，研究含有自由边界条件矩形板的屈曲失稳问题具有重要意义.鲍四元等[11]基于最小势能原理，计算了单向轴压作用下任意弹性边界矩形板的屈曲载荷系数，其中包括三边固支、一边自由等包含自由边界的情况，并给出了模拟不同边界条件时弹簧刚度的合理取值.刘寅华等[12]采用能量法以及非线性有限元法对加载对边简支，非加载边一边固支、一边自由的矩形薄板的屈曲强度进行了分析，并对比欧拉失稳和极值点失稳的临界应力，发现两者差异不大.该方法仅适用于特定边界条件，并不具有普适性.于海军等[13]利用辛弹性力学方法推导出了矩形带材局部纵向屈曲区域承受加载对边简支、非加载边一边简支、一边自由约束条件时的临界屈曲应力和屈曲挠度函数.而Li等[14,15]采用辛叠加方法，先后得出了四边自由和具有两个相邻自由边的双轴压缩矩形薄板屈曲失稳问题的解析解.与通常采用的半逆解法相比，辛弹性力学方法无需对解的形式进行假设，但其推导过程较为复杂.

有限差分法是一种数值解法，其有着简单、通用性强及在计算机程序上实现简便等优势.Ravari等[16]使用有限差分法研究了矩形纳米板的屈曲失稳特性，并与文献解进行比较，验证了有限差分法的有效性.袁坚锋等[17]基于Levy形式级数和有限差分法提出了面内弯曲载荷作用下两边简支、两边固支复合材料层合板的数值解法.该方法理论推导复杂，且只适用于特定边界条件，不能适用于包含自由边界条件矩形板的屈曲失稳问题求解.

目前，针对含对边自由边界矩形板屈曲失稳特性方面的研究工作较少.本文基于有限差分法对含对边自由边界矩形板的屈曲失稳特性展开研究.首先，针对不考虑剪切效应的矩形板屈曲控制微分方程及边界条件进行离散化，将求解临界屈曲载荷的问题转换为求解挠度系数矩阵广义特征值的问题；对比不同网格结点数下有限差分数值解、有限元仿真解与文献解之间的相对误差，验证本文求解方法的精确性.在此基础上，系统研究矩形板几何参数中边长比与厚宽比同有限差分法求解精度之间的耦合作用规律.针对厚宽比较大的矩形板，采用最小二乘法进行曲线拟合给出有限差分法精确求解的几何参数适用范围计算公式.最后，经过实例参数分析验证表明，有限差分法能在拟合公式限定的几何参数范围内精确求解含对边自由边界矩形板的屈曲失稳问题.

1 基本方程

受轴向压缩载荷作用下含对边自由边界矩形板的示意图如图1所示.在图1中：b为矩形板的宽度；l为矩形板的长度；F代表自由边界条件；Nx为其x方向上的轴向载荷.

基于弹性板的小挠度弯曲理论，各向同性矩形板的屈曲控制微分方程[18]：

(1)

式(1)中：D=Et3/[12(1-v2)]为矩形板的弯曲刚度；E为板的弹性模量；v为泊松比；t为板厚；w为挠度；Nx、Ny以及Nxy分别为x方向上的轴向载荷、y方向的上的轴向载荷、xy平面内的剪切载荷.

考虑矩形板仅承受x方向上的均匀分布轴向压缩载荷，即Ny=Nxy=0，则式(1)简化为

(2)

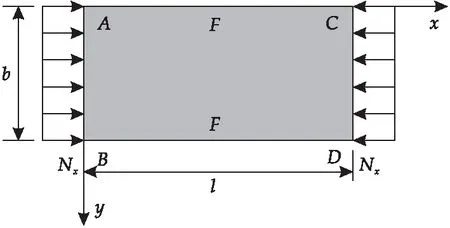
图1 含对边自由边界矩形板受载示意图

矩形板的典型边界条件包括固支、简支以及自由边界条件，图1中边AC、BD为自由边界，边AB、CD受简支或固支边界条件约束.以边x=0为例，以上三种边界条件可表示为

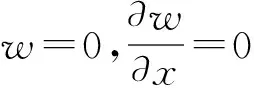
简支边：w=0,Mx=0

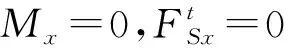
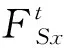
2 控制方程的有限差分法求解

有限差分法是应用离散的思想，用一个插值多项式及其微分来代替偏微分方程的解，首先需对求解区域进行网格划分，然后对方程中的导数进行充分近似，最后得到网格结点上未知函数的线性代数方程组并对其求解.

采用有限差分法对简化后的屈曲控制微分方程式(2)进行离散化处理.分别沿x、y方向将矩形板区域均匀划分成长度为Δx、宽度为Δy的网格，如图2所示.对于矩形板内任一结点的挠度wi,j的各阶差分公式可通过图2中相应的12个结点处的挠度按式(3)～(6)表示

一阶：

(3)

二阶：

(4)

三阶：

(5)

四阶：

(6)

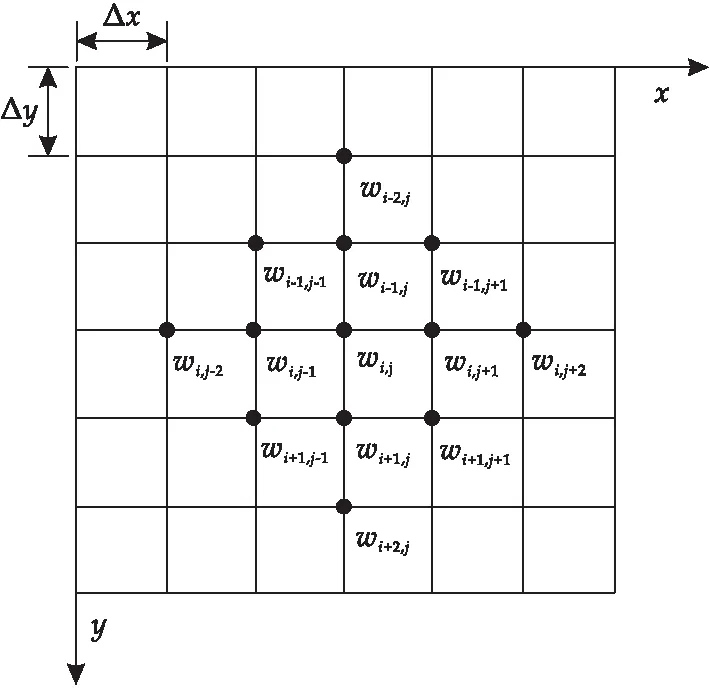
图2 结点划分示意图

将式(3)～(6)代入式(2)，得到板内各个结点处的以挠度为未知量的差分方程式(7).同时，根据矩形板及其边界条件的对称性，可对结点进行简化，减少独立结点数量.

i=1,2,…,n;j=1,2,…,m

(7)

式(7)中：n为矩形板y方向上结点数，m为矩形板x方向上结点数.

下文以轴向压缩载荷作用下非加载对边自由、加载对边简支矩形板为例，研究含对边自由边界矩形板的屈曲失稳特性.通过式(3)～(6)导出边界条件的差分形式：

自由边AC、BD：

(8(a))

(8(b))

对于简支边AB、CD，Mx=0可以简化为∂2w/∂x2=0:

wi,j=0

(9(a))

(9(b))

考虑到矩形板边界处结点的差分方程中包含板外虚结点挠度，应用边界条件，将板外虚结点用板内结点表示.

如图3所示，S、F分别代表简支、自由边界条件.考虑矩形板的两种边界条件，对自由边外由内到外第一行虚结点上任意结点4，第二行虚结点上任意结点12，以及简支边外第一列虚结点上任意结点20处的挠度可如式(10)表示

(10)

将式(10)带入差分方程式(7)，得到一个线性方程组，其矩阵形式为

(A+ηB)w=0

(11)

式(11)中：η=Nx/(DΔx2)；其中矩阵A、B由边界条件、网格划分、弯曲刚度等决定.求得式(11)挠度系数矩阵广义特征值的最小值ηcr，进而得到矩形板的临界屈曲载荷：

Ncr=ηcrDΔx2

(12)

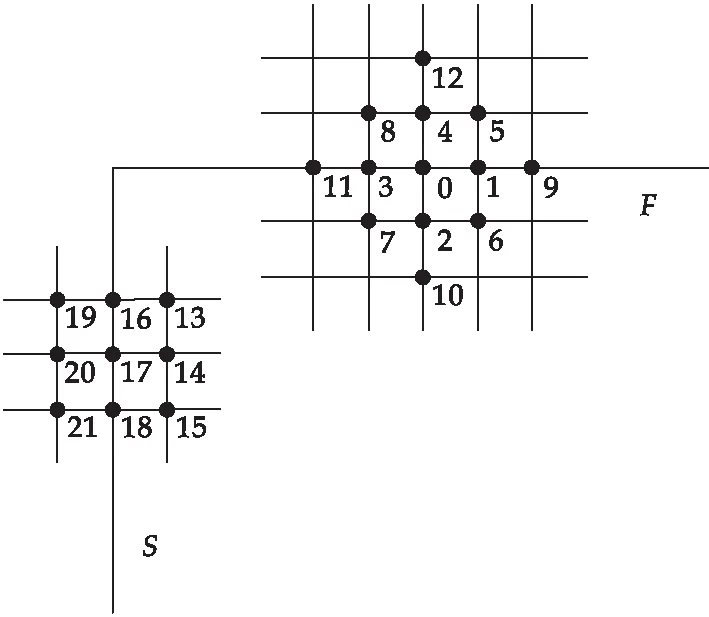
图3 边界外虚结点与边界内结点示意图

3 收敛性分析

基于MATLAB平台编程实现有限差分法求解矩形板的临界屈曲载荷，程序运行流程如图4所示.

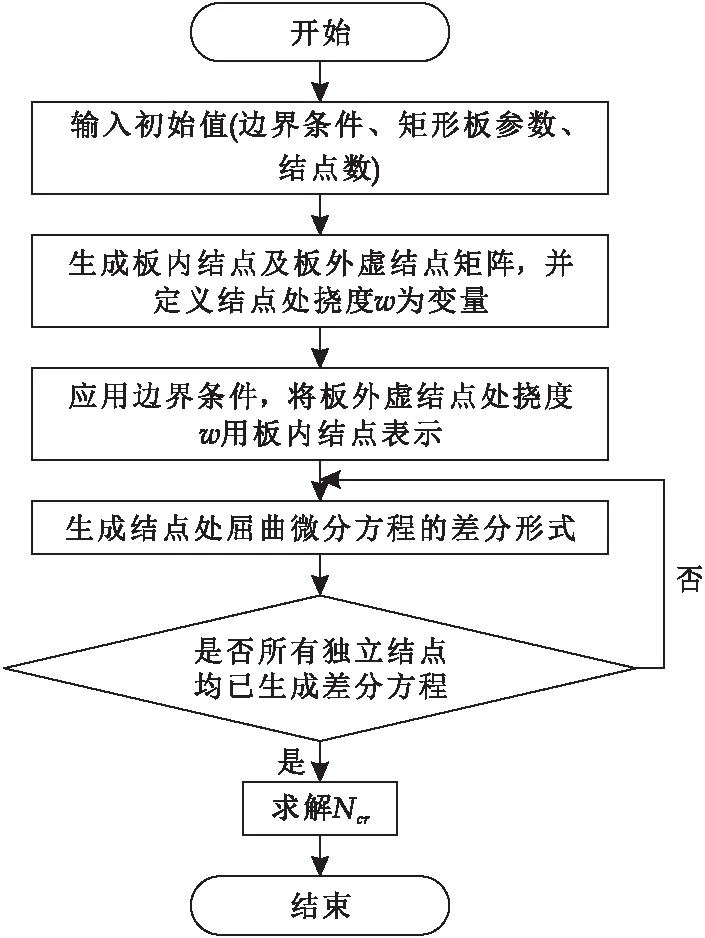
图4 MATLAB有限差分法程序流程图

计算中取x、y方向上的结点数相等(m=n).单向轴压作用下非加载对边自由、加载对边简支矩形板宽度b=1 m，厚宽比t/b=0.01.本文材料弹性模量E=70 GPa，泊松比v=0.3.分别采用有限差分法、有限元软件ABAQUS的buckle模块求解其临界屈曲载荷.ABAQUS有限元模型(r=1)如图5所示.ABAQUS有限元模型采用4结点减缩积分壳单元(S4R)，每个单元包含4个结点，在每个结点处有6个自由度(3个平动自由度，3个转动自由度).对于矩形板的左右两端采取简支约束并在右端施加轴向压缩载荷，上下两端不设置约束，使其作为自由边.

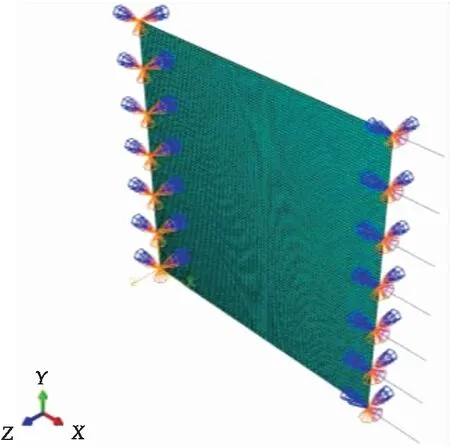
图5 有限元模型

当边长比r=1时，基于有限元法在不同结点数下求解单向轴压作用下非加载对边自由、加载对边简支矩形板的临界屈曲载荷与文献解之间的相对误差，结果如图6所示.随着结点数的增加，有限元仿真解逐渐收敛，结点数10 201、12 544分别对应单元尺寸的取值为0.01 m、0.009 m，当结点数取上述两值时，由图6可见，基于文献[19]求解结果的相对误差均为0.44%，而基于文献[20]求解结果的相对误差仅由0.36%变到0.35%，此时有限元仿真解具有较高精确性及稳定性，由此认为单元尺寸取值为0.01 m(结点数为10 201)时有限元仿真解收敛，后续有限元仿真相关计算均采用此单元尺寸.

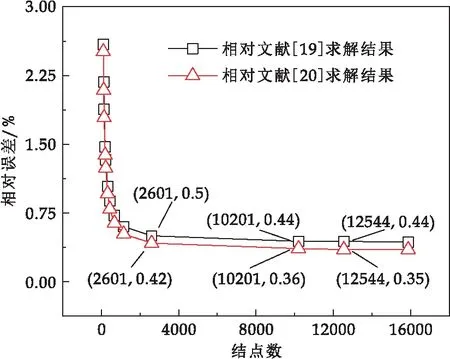
图6 有限元仿真解相对误差随结点数变化曲线

当边长比r=1时，基于有限差分法在不同结点数下求解单向轴压作用下非加载对边自由、加载对边简支矩形板的临界屈曲载荷与文献解之间的相对误差，结果如图7所示.随着结点数的增加，有限差分数值解呈收敛趋势，基于文献解的相对误差的绝对值随着结点数增加而逐渐减小，当结点数取20×20(m×n)时，基于文献[19]、[20]求解结果的相对误差分别为-0.15%、-0.23%.随着结点数的增加有限差分数值解精度逐渐提高，同时曲线斜率逐渐减小，当结点数由20×20变化到22×22时，各曲线中相对误差绝对值的变化值最大仅为0.04%，而后者所需计算时间却为前者的133.67%，为了在保证计算精度的前提下节约计算成本，后续计算中有限差分法离散结点数均取20×20.有限元仿真求解中，单元尺寸取值为0.01 m时包含10 201(r=1)个结点，且在每个结点处有6个自由度，其收敛速度以及计算效率远不如本文有限差分法求解程序.

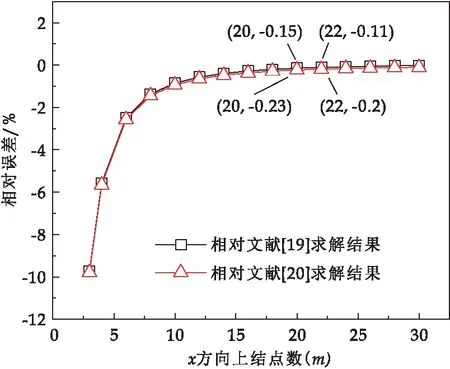
图7 有限差分数值解相对误差随结点数变化曲线

为进一步验证结点数取20×20时，有限差分法的适用性，在不同几何参数下，将有限差分数值解与文献解进行对比.如表1所示，有限差分数值解与文献[19]、文献[20]求解结果非常接近.

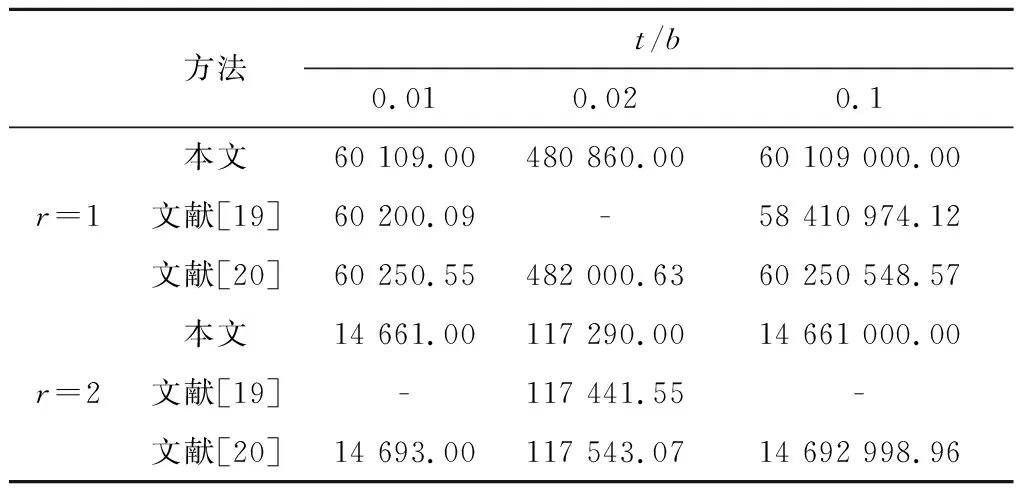
表1 不同几何参数下的临界屈曲载荷(N/m)

有限元仿真解易于获得，且能保证较高的精度，后文所述相对误差均基于有限元仿真解.当边长比0.1≤r≤5时，分别采用有限差分法与有限元法求得的临界屈曲载荷如图8所示.两种方法所得结果非常接近，有限差分数值解与有限元仿真解相对误差绝对值的最大值仅为0.84%，说明有限差分法具有较高的精确性.当边长比r=1时，有限元法得出临界屈曲载荷为60 467 N/m，有限差分法得出临界屈曲载荷为60 109 N/m，有限差分数值解相对误差绝对值仅为0.59%.边长比r=1时，有限差分法求解结果与有限元模型的一阶屈曲失稳模态对比如图9所示.由图9可见，有限差分法求解的屈曲失稳模态与有限元模型一致.

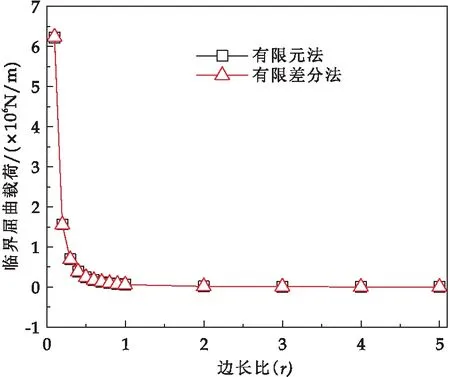
图8 临界屈曲载荷随边长比变化曲线

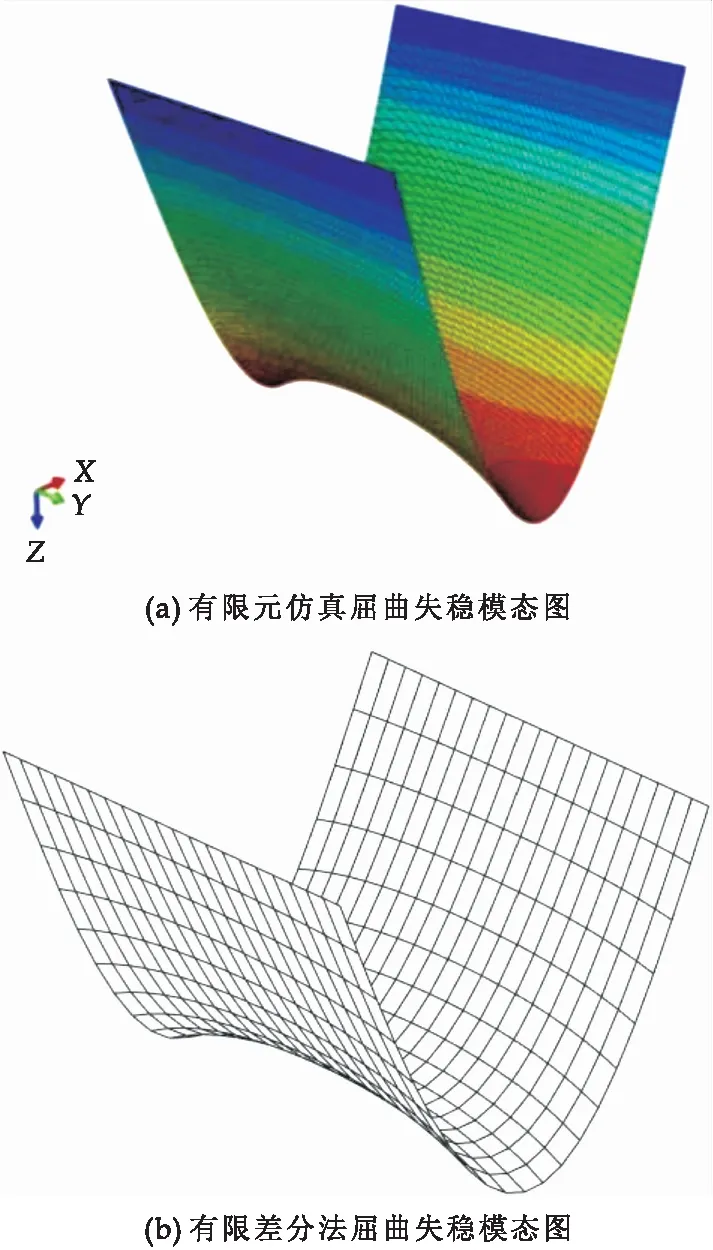
图9 t/b=0.01,r=1时矩形板的一阶屈曲模态图

4 误差分析

矩形板宽度b=1，厚宽比t/b分别取0.01～0.1，当边长比0.1≤r≤5时，以有限差分法求解单向轴压作用下非加载对边自由、加载对边简支矩形板为例研究有限差分数值解相对误差的变化规律，并考虑有限差分法精确求解矩形板屈曲临界载荷的几何参数适用范围.

4.1 几何参数变化对有限差分法求解精度的影响

不同厚宽比下有限差分数值解相对误差随边长比r变化曲线如图10所示.结果显示，随着边长比r的增大，有限差分法求解精度逐渐提高，当边长比r取值较小时，相对误差随边长比r增大而减小趋势比较剧烈；当边长比r取值较大时，相对误差随边长比r变化趋势较为平缓；当边长比r取值相同时，相对误差随着厚宽比的增大而增大.这是由于求解时忽略了板厚方向上的剪切效应，而随着厚宽比的增加，其影响也逐渐增大直至不可忽略，导致了相对误差的增大.从图10(a)可以看出，厚宽比取值较小时，相对误差随边长比r的增大先单调减小再单调增大，且相对误差会小于0，这是由于有限差分数值解偏小，如图7所示，结点数的增加可以减弱其影响，而厚宽比取值较大时忽略剪切效应的影响占主导，所以未呈现此现象，如图10(b)所示.

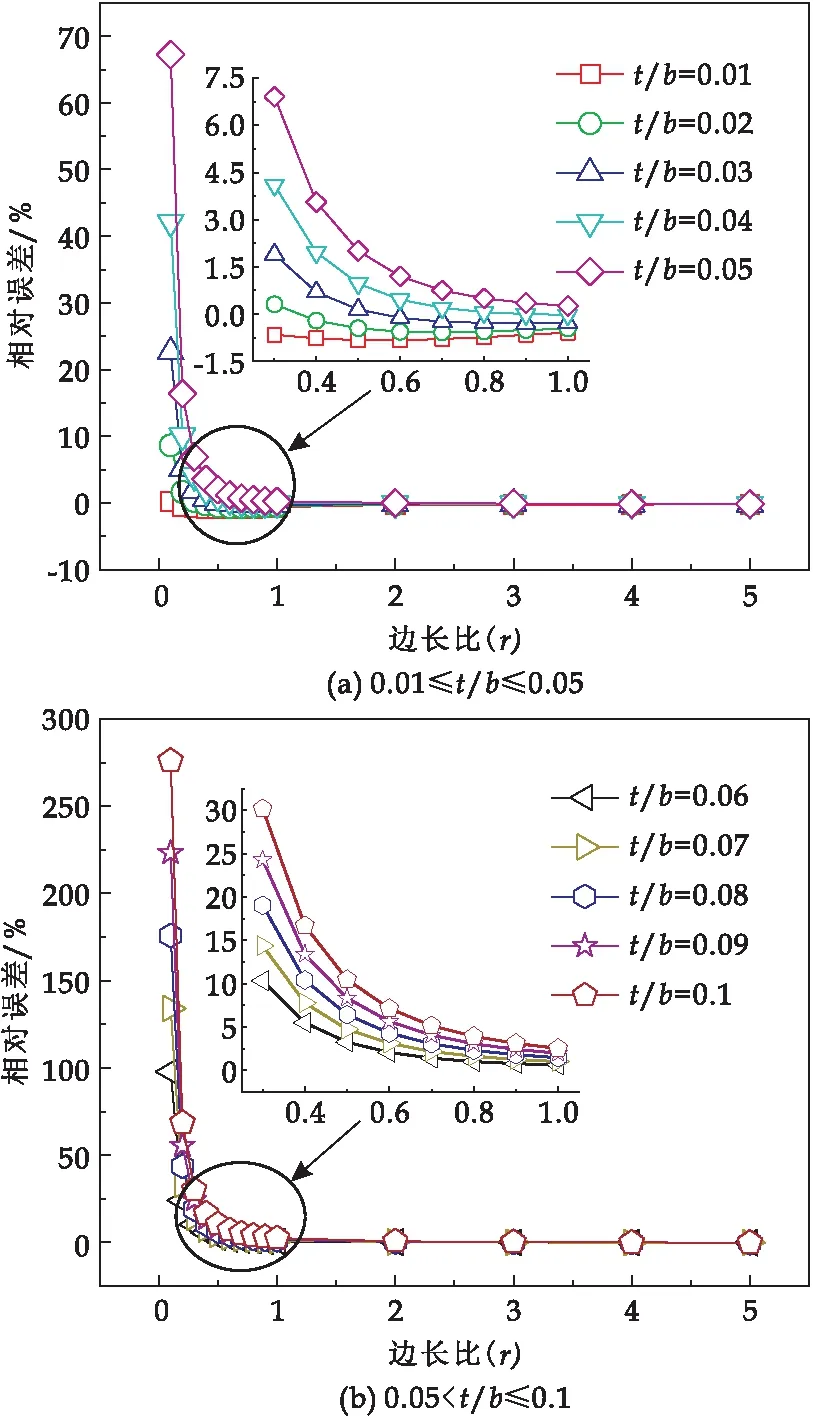
图10 边长比与厚宽比同相对误差之间的 耦合作用规律

4.2 几何参数精确求解适用范围计算公式的拟合

采用曲线拟合的最小二乘法得出各厚宽比下有限差分数值解相对误差与边长比的关系式，基于以上关系式得到一系列使相对误差略小于5%的矩形板几何参数.基于这一系列几何参数再次进行拟合，得到有限差分法精确求解矩形板屈曲失稳特性对应的几何参数适用范围计算公式：

(t/b)=0.126 6r+0.004 98

(13)

在已知厚宽比或边长比情况下，通过式(13)得出的矩形板几何参数可保证相对误差小于5%.为验证式(13)的准确性，取厚宽比分别为0.01，0.05，0.1，基于式(13)分别求得相应边长比；取边长比分别为0.5，1，2，5，基于式(13)求得相应厚宽比.记录以上式(13)计算结果及其相对误差.

不同厚宽比下有限差分数值解相对误差随边长比变化曲线如图11所示，式(13)计算得出各点相对误差均略小于5%，当边长比大于式(13)计算结果时，相对误差均在5%以下.图12显示了不同边长比下的有限差分数值解相对误差随厚宽比变化曲线，同样式(13)计算得出各点相对误差均略小于5%，当厚宽比小于式(13)计算结果时，相对误差不超过5%.综上，式(13)可精确计算有限差分法精确求解矩形板屈曲失稳问题的几何参数适用范围.

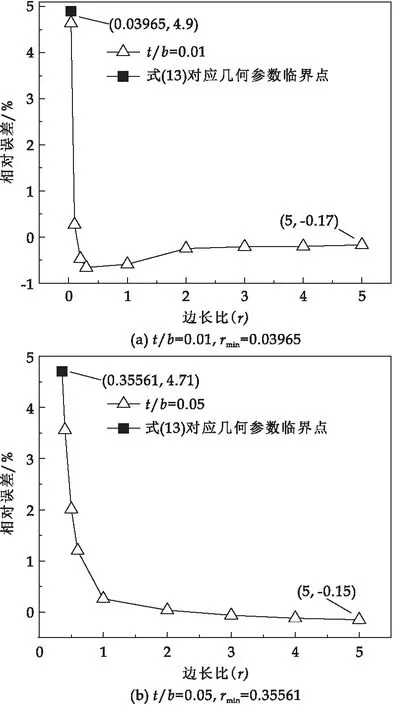
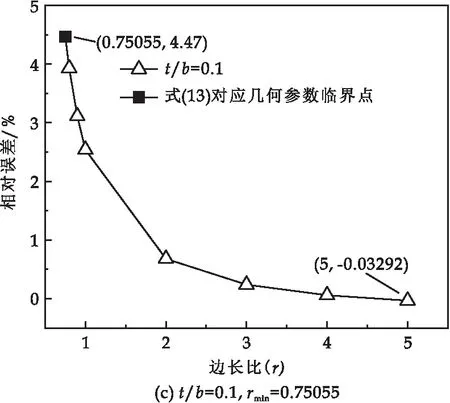
图11 当厚宽比t/b=0.01,0.05,0.1时,相对误差 随边长比变化曲线

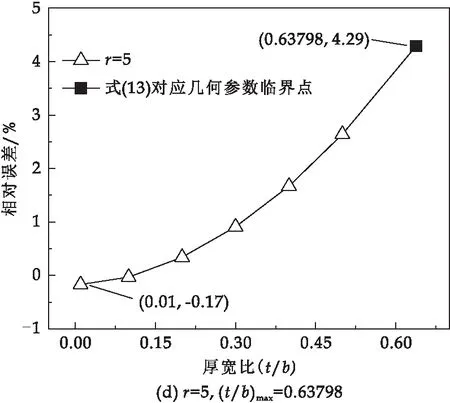
图12 当边长比r=0.5,1,2,5时,相对误差 随厚宽比变化曲线

5 结论

本文采用有限差分法，以单向轴压作用下非加载对边自由、加载对边简支矩形板为例，对含对边自由边界矩形板的屈曲失稳特性进行了研究，得到以下主要结论：

(1)有限差分数值解随结点数的增加逐渐收敛，且具有较高计算效率.通过与文献解、精确的有限元仿真解之间的对比分析，验证了有限差分法的精确性.

(2)当厚宽比一定时，有限差分法求解的相对误差会随着边长比的增大而减小；当边长比一定时，由于剪切效应的影响有限差分数值解相对误差会随着矩形板厚宽比增大而增大.

(3)有限差分法能够在拟合公式给出的几何参数适用范围内，精确求解含对边自由边界矩形板的屈曲失稳问题，使其相对误差保持在给定范围内.