李燕清，黄俊杰，*，阿拉坦仓

(1.内蒙古大学 数学科学学院，内蒙古呼和浩特 010021;2.内蒙古师范大学 数学科学学院，内蒙古呼和浩特 010022)

§1 引言

算子矩阵常常出现于系统理论，最优控制，应用力学以及数学物理等研究领域.众所周知，算子矩阵的Fredholm理论，特征向量展开定理等谱问题的研究比较复杂，一直没有彻底解决.为研究这类问题，往往需要引入一些有效的工具和研究方法.通常，算子矩阵可以分解为一个斜对角算子矩阵和一个具有良好性质的算子矩阵之和.因此，斜对角算子矩阵有望成为研究这些谱问题的有力工具，其中谱性质是亟需解决的关键问题之一.

近年来，许多学者研究了斜对角算子矩阵H的谱性质，并得到一些有意义的结论.在文[1]中，当B和C均自伴，即H为Hamilton算子矩阵时，得到了点谱的描述

并且0(H)当且仅当0(B)∪σp(C);而当其同时满足(BC)*CB时，有剩余谱和连续谱的刻画

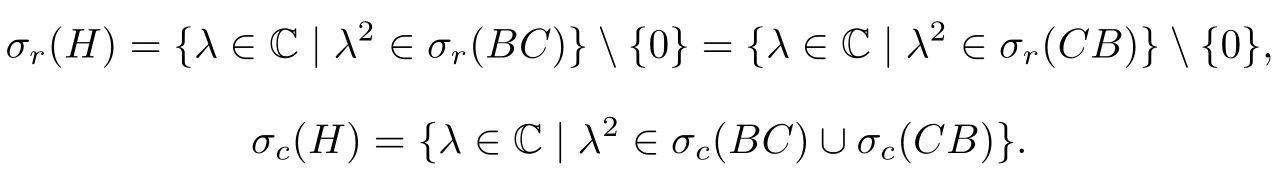
对于一般的有界算子B和C，文[2]给出近似点谱的描述

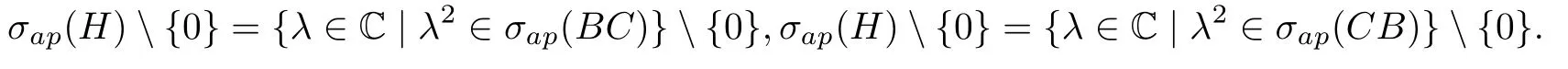
在文[3]中，当B和C是自伴算子时，

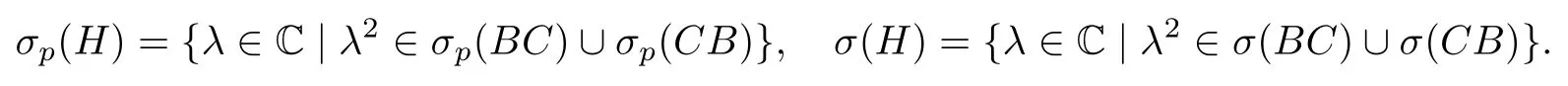
当B和C是可逆算子时，文[4]给出了本质谱的刻画σe(H){C|λ2(BC)∪σe(CB)}.

综上所述，在一定的条件下，可以通过斜对角算子矩阵中两个斜对角元的之积BC和CB的谱性质刻画整个算子矩阵的谱性质.目前为止，未见斜对角算子矩阵的左(右)Weyl谱和Weyl谱的相关研究，本文基于算子积的Fredholm性与各因子的关系解决了这个问题.

§2 预备知识

本文涉及的算子均为线性算子，对于算子T，分别以N(T)和R(T)表示零空间和值域;记n(T)dimN(T)，d(T)codimR(T).

定义2.1(见[5])X，Y为Banach空间，若T:X →Y是具有闭值域的稠定闭算子，n(T)＜∞，则称T为左Fredholm算子;而若零性条件替换为d(T)＜∞，则称T为右Fredholm算子;若T既是左Fredholm算子又是右Fredholm 算子，则称T为Fredholm算子;若T是左Fredholm算子或者右Fredholm算子，则称T为半Fredholm算子，此时可定义它的指标i(T)n(T)-d(T)，其中i(T)取值可为±∞.

定义2.2(见[5])X为Banach空间，T是X中的算子.若T -λI不是左(右)Fredholm算子，则λ称为T的左(右)本质谱，左(右)本质谱的全体记为σle(T)(σre(T));若T -λI不是Fredholm算子，则λ称为T的本质谱，本质谱的全体记为σe(T).

定义2.3(见[5–7])X，Y为Banach空间，若T:X →Y为左Fredholm算子且i(T)≤0，则称T为左Weyl算子;若T为右Fredholm算子且i(T)≥0，则称T为右Weyl算子;若T为Fredholm算子且i(T)0，则称T为Weyl算子.

定义2.4(见[5–7])X为Banach空间，T为X中的算子.若T-λI不是左(右)Weyl算子，则λ称为T的左(右)Weyl谱，左(右)Weyl谱的全体记为σlw(T)(σrw(T));若T-λI不是Weyl算子，则λ称为T的Weyl谱，Weyl谱的全体记为σw(T).

定义2.5(见[8])X为Hilbert空间，H:D(H)⊆X ⊕X →X ⊕X是稠定闭算子，其中A为闭算子，B和C均为自伴算子，则称H为Hamilton算子矩阵.

引理2.1(见[5])X，Y，Z为Banach空间，S:X →Y和T:Y →Z均为Fredholm算子，则TS:X →Z是Fredholm算子且i(TS)i(T)+i(S).

引理2.2(见[5])X，Y，Z为Banach空间，若S:X →Y和T:Y →Z均为左Fredholm算子且D(TS)在X中稠定，则TS:X →Z是左Fredholm算子;若S:X →Y和T:Y →Z均为右Fredholm算子且TS可闭，则TS:X →Z是右Fredholm算子.

引理2.3(见[5])X，Y，Z为Hilbert空间，S:X →Y是右Fredholm算子，T:Y →Z是稠定算子，则TS:X →Z稠定且(TS)*S*T*.

引理2.4(见[9])X，Y，Z为Hilbert空间，S:X →Y，T:Y →Z均为稠定闭算子.若TS:X →Z是右Fredholm算子，则T是右Fredholm算子;若TS:X →Z是左Fredholm算子且(TS)*S*T*，则S是左Fredholm算子.

引理2.5(见[10])X，Y是Hilbert空间，T:X →Y是稠定闭算子，则T*T，TT*均为自伴算子.

§3 主要结果

在本节中，如无特别说明X均为无穷维Hilbert空间，首先考虑斜对角算子矩阵

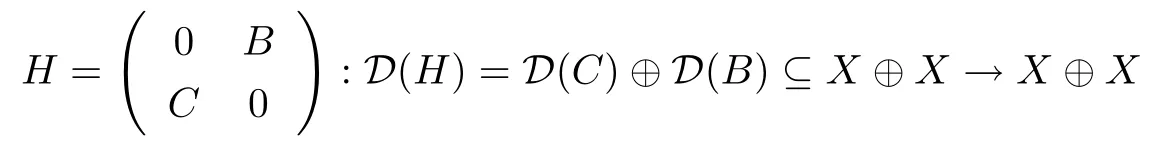
Weyl谱的刻画.

证假设λ不在上式等号右端的集合中，则H -λI为Fredholm算子且

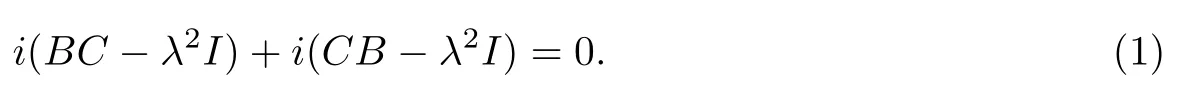
注意到斜对角算子矩阵H满足

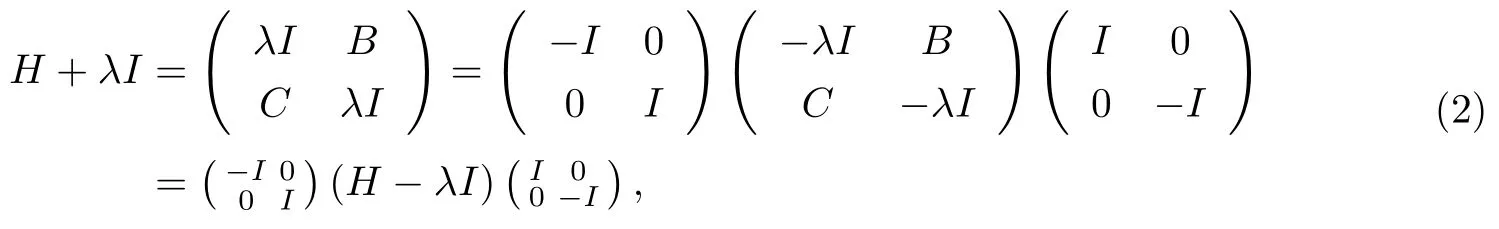
显然H+λI为Fredholm算子，应用引理2.1有H2-λ2I是Fredholm算子且

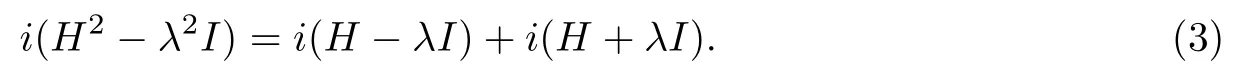
因为

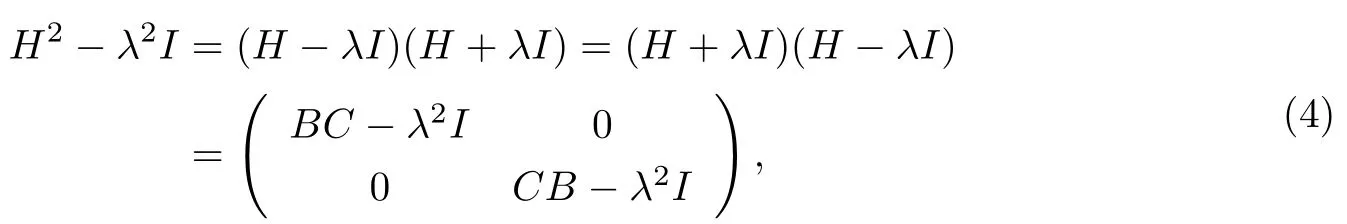
所以

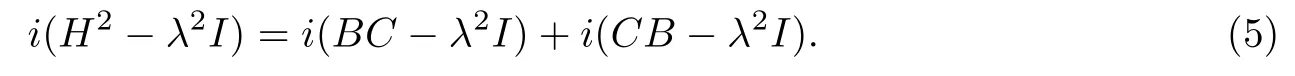
结合(1)，(3)，(5)得

另一方面，又由(2)显然

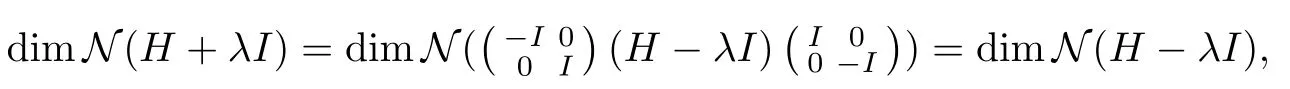
从而

因此

结合(7)，(8)得

进而由(6)，(9)有i(H -λI)0. 于是H -λI为Weyl算子，即(H).综上证明了

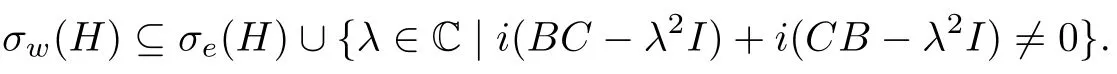
下面证明相反的包含关系.为此假设(H).注意到(2)，由前述证明有(H)，因此H -λI，H+λI均为Weyl算子，即H -λI，H+λI均为Fredholm算子且

由引理2.1，H2-λ2I也是Fredholm算子且满足指标公式:

结合(5)，(10)，(11)有

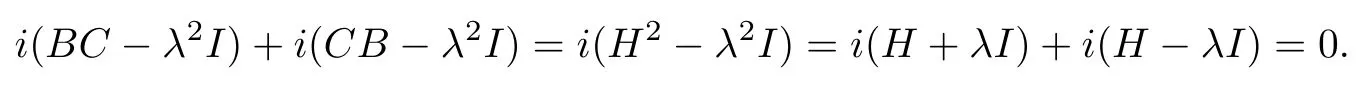
于是(H)且{C|i(BC-λ2I)+i(CB-λ2I)0}.综上

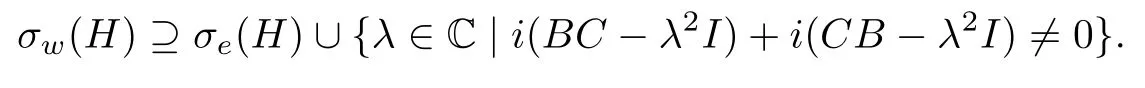
由定理3.1的证明过程，实际上还有推论3.1.

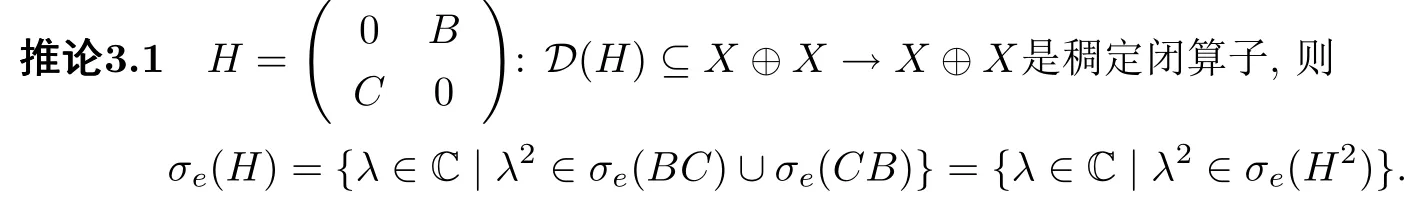
结合定理3.1和推论3.1有

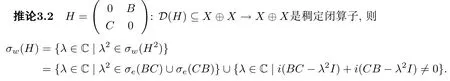
下面讨论左Weyl谱，由于涉及两算子积的左Fredholm性，需要一些附加条件.

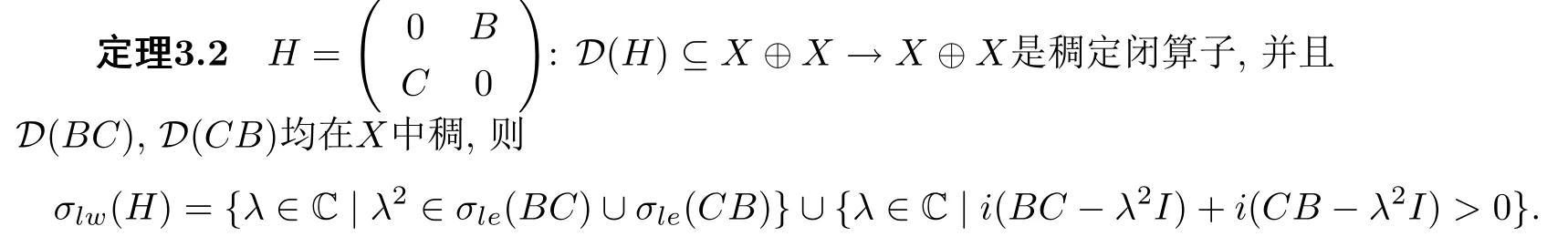
证假设λ不在上式等号右端的集合中，则BC-λ2I，CB-λ2I均为左Fredholm算子，同时

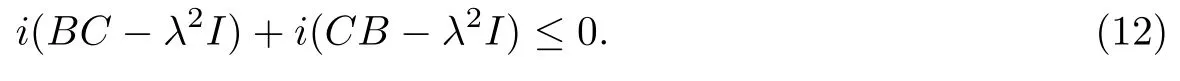
由(4)，显然有H2-λ2I是左Fredholm算子，并且

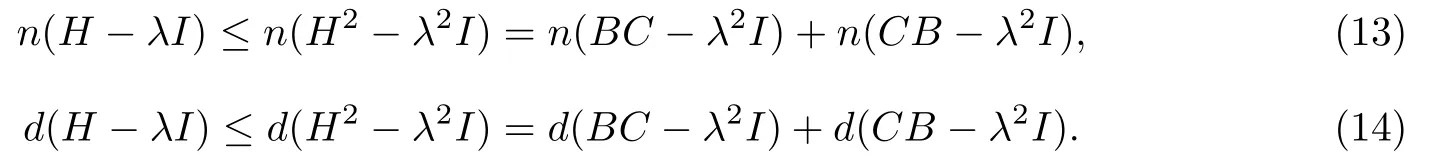
注意到H -λI和H+λI可交换，由引理2.4得到H -λI，H+λI均为左Fredholm算子.以下分两种情形讨论:

情形1d(H-λI)＜∞.此时由(8)有d(H+λI)＜∞，故H-λI，H+λI均为Fredholm算子.结合(5)，(12)和引理2.1得

注意到(9)有i(H -λI)≤0.因此，H -λI为左Weyl算子.

情形2d(H -λI)∞.此时，n(H -λI)＜d(H -λI)，即

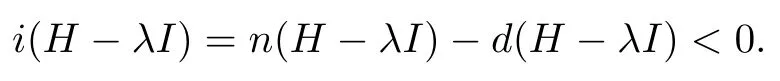
因此H -λI为左Weyl算子.综上(H)，于是

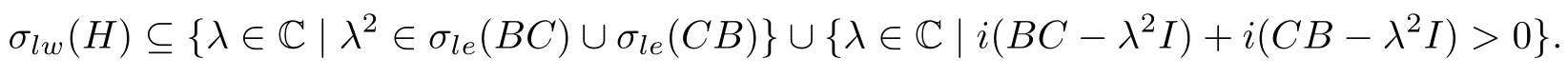
下面证明相反的包含关系.假设(H)，由(2)有(H)，因此H -λI，H+λI均为左Weyl算子，显然它们均为左Fredholm算子，并且结合(9)还有

注意到D(H2)D(BC)⊕D(CB)在X ⊕X中稠，应用引理2.2得到H2-λ2I是左Fredholm算子，由(4)这等价于BC-λ2I，CB-λ2I均为左Fredholm算子.以下分两种情形讨论:

情形1d(H2-λ2I)＜∞.此时，由(8)和(14)得d(H-λI)d(H+λI)＜∞，从而H-λI，H+λI均为Fredholm算子.结合(5)和(15)，应用引理2.1便有

情形2d(H2-λ2I)∞.此时，显然n(H2-λ2I)＜d(H2-λ2I)，即

证假设λ不在上式等号右端的集合中，则BC-λ2I，CB-λ2I均为右Fredholm算子，同时

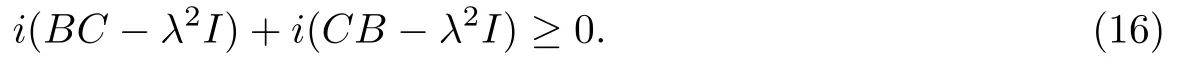
显然，R(BC-λ2I)，R(CB-λ2I)均为闭的，dim[(BC-λ2I)]＜∞，dim[(CB-λ2I)]＜∞.由类似于(14)的值域余维数的不等式，有dim[(X ⊕X)(H-λI)]＜∞(从而R(H-λI)闭)，因此H -λI为右Fredholm算子.同理，H+λI也为右Fredholm算子.以下分两种情形讨论.

情形1n(H-λI)＜∞.此时，由(7)有n(H+λI)＜∞，因此H-λI，H+λI均为Fredholm算子，结合(5)，(16)和引理2.1得

又由(9)有i(H -λI)≥0.因此，H -λI为右Weyl算子.

情形2n(H -λI)∞.此时显然n(H -λI)＞d(H -λI)，从而i(H -λI)＞0.因此H -λI为右Weyl算子.综上(H).于是，

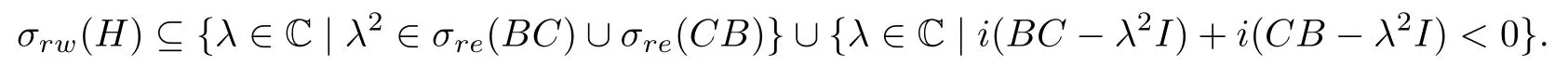
下面证明相反的包含关系.假设(H)，由(2)知(H)，则H-λI，H+λI均为右Weyl算子，因此H -λI，H+λI均为右Fredholm算子，又由(9)有

根据引理2.3和引理2.2，H2-λ2I为右Fredholm算子，这等价于BC -λ2I，CB -λ2I均为右Fredholm算子.以下分两种情形讨论:

情形1n(H2-λ2I)＜∞.此时，由(7)和(13)有n(H-λI)n(H+λI)＜∞，所以H-λI，H+λI均为Fredholm算子，由(5)，(17)和引理2.1得

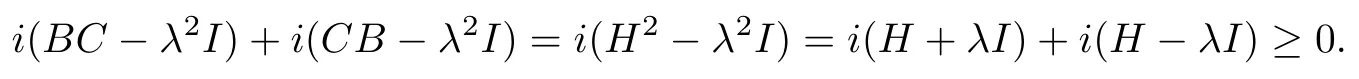
情形2n(H2-λ2)∞.此时n(H2-λ2)＞d(H2-λ2)，即

证由定理3.3的证明过程直接可得.

事实上，当λ0时，从B，C的谱性质考虑，有以下简要结果.

(i) 0(H)⇔0(B)∪σe(C)，或i(B)+i(C)0.

(ii) 0(H)⇔0(B)∪σle(C)，或i(B)+i(C)＞0.

(iii) 0(H)⇔0(B)∪σre(C)，或i(B)+i(C)＜0.

证(i) 充分性若B，C都是Fredholm算子且i(B)+i(C)0，则H是Fredholm 算子，根据i(H)i(B)+i(C)0，可得H是Weyl算子.

必要性若H是Weyl算子，即H是Fredholm算子且i(H)0，则B，C都是Fredholm算子，i(B)+i(C)i(H)0.类似可证明结论(ii)和(iii).

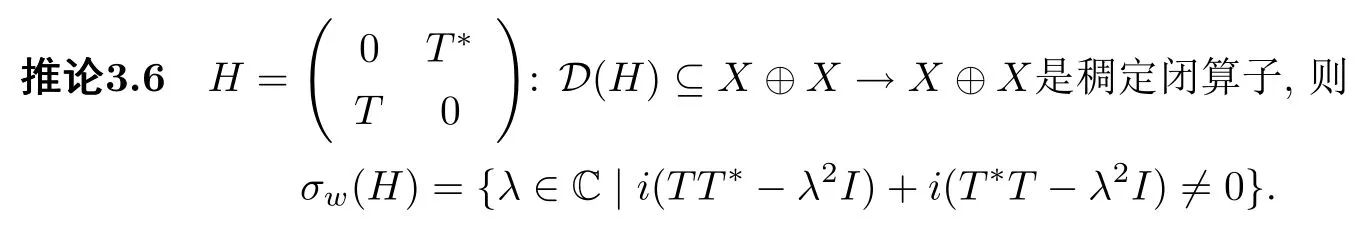
证注意到引理2.5，根据定理3.1的证明过程，结论显然成立.

注若HD(H)⊆X ⊕X →X ⊕X是Hamilton算子矩阵，则以上定理及推论均成立.