陆青

［摘  要］ 利用图形旋转可以巧妙地求线段长度的最值，求三条线段和的最值，求四边形面积的最值. 等线段共点、旋转问题、四边形中的等边共点且对角互补或为定值等都是适合利用图形旋转解题的特征.

［关键词］ 图形旋转；等边共点；最值

利用图形旋转可以巧妙地解题，有些求最值的题型就适合利用图形旋转来求解，如求线段长度的最值，求四边形面积的最值等，下面笔者通过举例探讨适合利用图形旋转解决的题型及求解方法.

题型1：求线段长度的最值

【方法1：利用等线段共点旋转后能够重合的特性进行图形旋转，构造折线段.】

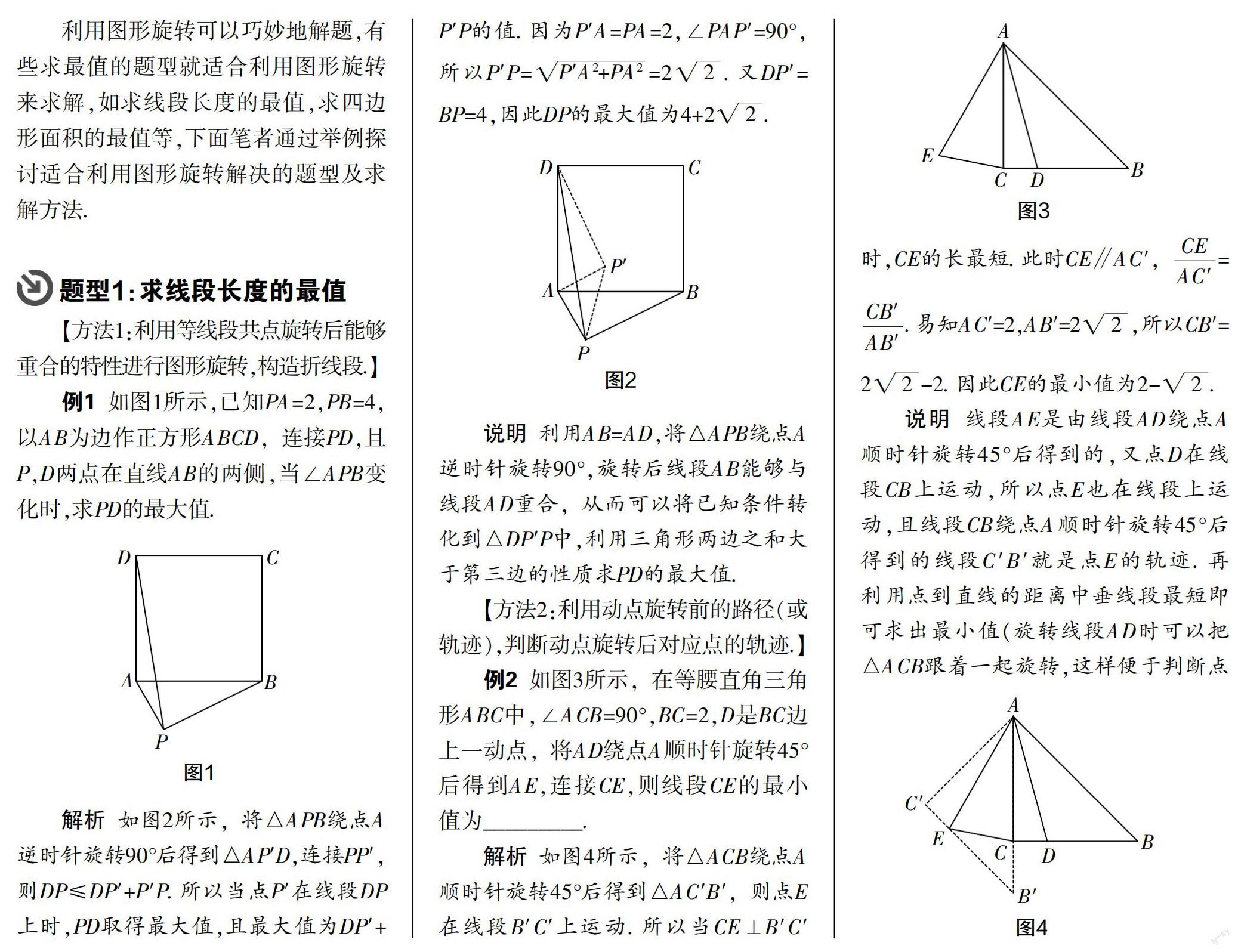
例1如图1所示，已知PA=2，PB=4，以AB为边作正方形ABCD，连接PD，且P，D两点在直线AB的两侧，当∠APB变化时，求PD的最大值.

解析如图2所示，将△APB绕点A逆时针旋转90°后得到△AP′D，连接PP′，则DP≤DP′+P′P. 所以当点P′在线段DP上时，PD取得最大值，且最大值为DP′+P′P的值. 因为P′A=PA=2，∠PAP′=90°，所以P′P==2. 又DP′=BP=4，因此DP的最大值为4+2.

说明利用AB=AD，将△APB绕点A逆时针旋转90°，旋转后线段AB能够与线段AD重合，从而可以将已知条件转化到△DP′P中，利用三角形两边之和大于第三边的性质求PD的最大值.

【方法2：利用动点旋转前的路径（或轨迹），判断动点旋转后对应点的轨迹.】

例2如图3所示，在等腰直角三角形ABC中，∠ACB=90°，BC=2，D是BC边上一动点，将AD绕点A顺时针旋转45°后得到AE，连接CE，则线段CE的最小值为_________.

解析如图4所示，将△ACB绕点A顺时针旋转45°后得到△AC′B′，则点E在线段B′C′上运动. 所以当CE⊥B′C′时，CE的长最短. 此时CE∥AC′，=. 易知AC′=2，AB′=2，所以CB′=2-2. 因此CE的最小值为2-.

说明线段AE是由线段AD绕点A顺时针旋转45°后得到的，又点D在线段CB上运动，所以点E也在线段上运动，且线段CB绕点A顺时针旋转45°后得到的线段C′B′就是点E的轨迹. 再利用点到直线的距离中垂线段最短即可求出最小值（旋转线段AD时可以把△ACB跟着一起旋转，这样便于判断点E的轨迹）.

例3  如图5所示，BD，AC为四边形ABCD的对角线，CD=2，∠CAD=60°，∠CAB=90°，∠CBA=30°，则BD的最大值为_________.

解析如图6所示，点A在以点O为圆心、为半径的圆上运动，CB可看作由CA先绕点C逆时针旋转60°，再扩大2倍后得到的. 于是将△ACD和☉O先绕点C逆时针旋转60°，再扩大2倍后得到△BCD′和☉O′，则点B在☉O′上运动，且☉O′的半径为. 连接O′C，O′B，O′D，则BD≤O′D+O′B. 所以当点O′在线段BD上时，BD取得最大值. 因为∠OCD=30°，∠O′CO=60°，所以∠O′CD=90°. 所以O′D==. 又O′B=，所以BD的最大值为.

说明∠CAD为定值，∠CAD所对的边CD也为定值，因此点A的轨迹是以线段CD为弦、所对的圆周角为60°的圆弧. 线段CB是由线段CA先绕点C逆时针旋转60°，再扩大2倍后得到的，又因为点A的轨迹为圆弧，所以点B的轨迹也是圆弧. 利用点到圆的距离中过圆心最大即可求出最大值（线段CA旋转并放大时，可以把△CAD及其外接圆弧一起跟着旋转并放大，这样便于判断点B的轨迹）.

题型2：求三条线段之和的最值

【方法：利用含三条线段中两条线段的三角形旋转60°得到等边三角形，将三条线段转化为一条折线段.】

例4如图7所示，在Rt△ACB中，∠ACB=90°，AC=2，BC=4，P在△ACB内部，且∠APC=120°，求AP+BP+CP的最小值.

解析如图8所示，将△CPA绕点C逆时针旋转60°后得到△CP′A′，连接PP′，A′B，则△PCP′是等边三角形. 所以∠CP′P+∠CP′A′=180°. 所以P，P′，A′三點共线. 所以AP+BP+CP=BP+PA′≥BA′. 所以当点P在线段BA′上时，AP+BP+CP取得最小值. 过点A′作A′E⊥BC交BC的延长线于点E，容易求得∠A′CE=30°，所以A′E=，CE=3，BE=7. 所以BA′==2. 因此AP+BP+CP的最小值为2.

说明将△CPA绕点C向△ABC外侧旋转60°（图中为逆时针方向）后得到等边三角形CPP′，于是将三条线段转化为一条折线段，最后利用“两点之间，线段最短”即可求出最小值. 本题由于P，P′，A′三点共线，所以利用三角形两边之和大于第三边来求最小值（点P为费马点）.

例5如图9所示，矩形ABCD的边AD上有一动点F，矩形内有一动点E，AB=2，BC=4，求EF+EB+EC的最小值.

解析如图10所示，将△CEB绕点C逆时针旋转60°后得到△CE′B′，则当B′，E′，E，F四点共线且B′F⊥AD时（如图11所示），EF+EB+EC取得最小值，且最小值为2+2.

说明将△CEB（它由三条线段中的两条线段与矩形的一边构成）绕点C向矩形ABCD外侧旋转60°（图中为逆时针方向）后得到等边三角形CEE′，将三条线段转化为一条折线段，利用点到直线的距离中垂线段最短即可求出最小值.

题型3：求四边形面积的最值

【方法1：利用四边形有共点的等边，且对角互补，把求四边形面积的最值转化为求三角形面积的最值.】

例6如图12所示，在四边形ABCD中，AB=AD，∠B+∠D=180°. 若AC=2，则四边形ABCD的面积的最大值为______.

解析如图13所示，将△ADC绕点A顺时针旋转后得到△ABC′，则C′，B，C三点共线，四边形ABCD的面积等于△ACC′的面积. 因为△ACC′的边AC′上的高h≤AC，所以S=·AC′·h≤·AC′·AC. 又AC′=AC=2，所以△ACC′的面积的最大值为2. 所以四边形ABCD的面积的最大值为2.

说明利用AB=AD，以点A为旋转中心旋转△ADC，使旋转后AD与AB重合，并利用∠B+∠D=180°，得到C′，B，C三点共线，于是把求四边形ABCD的面积的最大值转化为求△ACC′的面积的最大值.

【方法2：利用四边形有共点的等边，且对角为定值，把求四边形面积的最值转化为求两个三角形面积之差的最值.】

例7如图14所示，在四边形ABCD中，AD=CD，∠ABC=60°，∠ADC=60°，BD=3，则四边形ABCD的面积的最小值为_________.

解析如图15所示，将△DAB绕点D逆时针旋转60°后得到△DCB′，连接BB′，则△DBB′为等边三角形，且面积为，∠BCB′=120°. 所以点C在以BB′为弦，且所对的圆周角为120°的圆弧上运动. 所以S=S+S=S-S. 所以当△CBB′的面积最大时，四边形ABCD的面积最小. 此时△CBB′为等腰三角形，面积为. 所以四边形ABCD的面积的最小值为.

说明利用AD=CD，以点D为旋转中心旋转△DAB，使旋转后DA与DC重合，再利用∠BCB′=120°为定值，得到点C的轨迹为圆弧，把求四边形ABCD的面积的最小值转化为求△DBB′与△CBB′面积之差的最小值.

求线段长度的最值，可利用共点的等线段，通过旋转图形构造折线；求三条线段之和的最值，可通过旋转图形60°，利用等边三角形将三条线段转化为一条折线段；求四边形面积的最值，可利用共点的等边且对角互补或为定值旋转图形，把求四边形面积的最值转化为求三角形面积的最值，或转化为求两个三角形面积之差的最值.