陆春燕

［摘  要］ 几何性质定理的教学要把握好知识联系，合理设计情境问题引入课堂，精心设置探究环节，引导学生完成定理的探究论证，使学生掌握定理的同时提升素养. 文章以“线段的垂直平分线的性质”为例，展开教学探讨.

［关键词］ 垂直平分线；性质；联系；探究；思想

“线段的垂直平分线的性质”是初中几何的重要内容，对几何知识体系的构建有着重要的意义. 探究教学需要教师引导学生掌握垂直平分线的性质及判断方法，要求学生能够灵活运用性质、定理解决实际问题，同时教学中教师还要落实核心素养，提升学生的综合能力. 下面基于教材内容展开教学反思.

把握知识联系，情境设计引入

“线段的垂直平分线的性质”是所学章节的重点，对于全新的知识，学生不知从何处开始探究，因此，在探索引入阶段，教师可以采用下面两种方式：一是从知识联系视角入手，关注知识的前后联系；二是从情境视角入手，精心选择情境素材，设计贴近学生生活的场景，引导学生逐步感知生活中的几何性质.

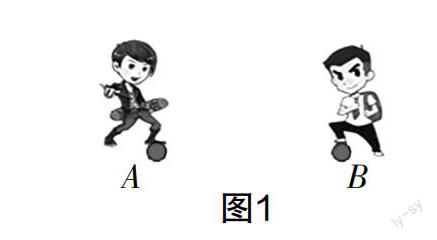
“线段的垂直平分线的性质”的教学核心是一条线、两端点、距离相等，情境问题可以从“距离相等”衍生出“公平”，从而设计实际问题引导学生思考，引出垂直平分线的性质. 所以教师可以设计如下问题：如图1所示，小明在点A处，小刚在点B处，两人在玩抢礼物的游戏. 为了保证游戏公平，礼物应放在什么地方？教学时教师应引导学生发散思维，思考除了可以放在线段AB的中点处外，还可以放在哪些地方，从而引出线段垂直平分线的性质.

該章节的知识内容，是在线段垂直平分线的概念和轴对称性质基础上的进一步探究，故教学线段的垂直平分线的性质时，教师有必要进行知识回顾、问题设计等教学设计. 问题设计建议采用递进设问的方式，引导学生逐步深入. 基于“线段AB展示→轴对称分析→作垂直平分线”来构建的问题链如下.

问题1：图2所示的线段AB是轴对称图形吗？

问题2：请指出图2中线段AB的垂直平分线.

问题3：可以采用哪些方法来绘制线段AB的垂直平分线？

教学中，教师要引导学生从轴对称的视角看待线段AB，深刻体会线段的轴对称性质. 在此基础上，教师要让学生思考线段垂直平分线的作法，引导学生采用测量、翻折两种方法来作线段的垂直平分线. 其中测量法分“取中点”“作垂直”两步，翻折方法则渗透了轴对称的性质. 整个教学过程教师要充分结合“操作实践”与“引导思考”，让学生在实践中重温垂直平分线的概念、轴对称的性质等知识，体会知识的生长过程，逐步过渡到性质探究.

重视探究过程，精设探究环节

“线段的垂直平分线的性质”属于几何性质探究内容，教学中建议教师精心设计各个环节，引导学生体验新知的获得过程，充分调动学生的思维，使学生掌握几何性质的同时获得思维的提升. 故教学中建议教师采用过程探究的方式，让学生参与活动.

性质探究需要完成“猜想验证”到“结论归纳”整个闭环过程，即教师要引导学生分析直观图形，做出猜想，然后利用相关知识验证，从中提取结论完成性质归纳. 设计教学环节时需要遵循两大原则：一是关注学情，把握学生的认知规律，让知识自然生成；二是丰富探究过程，注重思维引导，提升学生的思维水平. 教师教学“线段的垂直平分线的性质”时，可设计如下探究活动.

1. 活动1：分析关系，问题猜想

在“性质猜想”环节，教师需要引导学生直观感知，通过独立思考来做出猜想，故教学时建议设计图形问题，直观对比其中的数量关系，引导学生猜想.

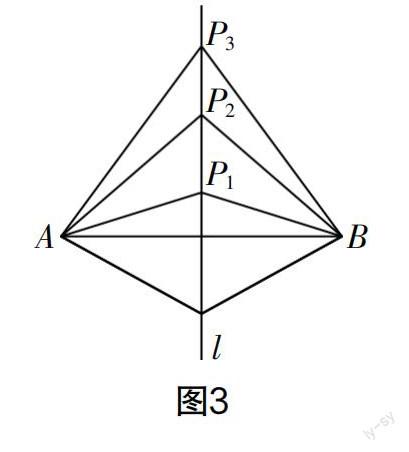
预设：给出如图3所示的图形，假定直线l为线段AB的垂直平分线，P1，P2，P3均是直线l上的点，观察P1，P2，P3三点到点A和点B的距离，分析其中的数量关系.

引导设计：此环节需要学生理解其中的位置关系，即l是AB的垂直平分线，故该直线经过AB的中点，并与AB垂直. 接着直接探讨线段之间的数量关系，即AP1与BP1、AP2与BP2、AP3与BP3之间的数量关系. 学生通过观察，可以初步感知到它们的长度相等，即线段AB垂直平分线上的P1，P2，P3三点到点A和点B的距离相等.

2. 活动2：动手操作，推理验证

“猜想验证”环节是基于上述猜想进行的探究验证，该环节要结合感性分析与理性推理，引导学生多角度论证，故可采用操作实践、几何证明两种方式进行教学.

（1）操作验证：测量、对折.

教学中，教师可引导学生用直尺分别测量AP1，BP1，AP2，BP2，AP3，BP3的长度，进而得出结论. 也可以沿直线l折叠线段AB，让学生观察AP1与BP1、AP2与BP2、AP3与BP3是否重合. 显然，若两两重合，则表示它们分别相等.

（2）几何证明：全等性质.

教师还可以引导学生通过判断对应三角形全等的方法来完成证明. 假定线段AB的中点为C，以分析△AP1C和△BP1C为例，教师可引导学生证明这两个三角形全等. 从已知出发，因为C是线段AB的中点，所以AC=BC. 因为直线l是线段AB的垂直平分线，所以∠P1CA=∠P1CB=90°，结合P1C=P1C，可得△AP1C≌△BP1C（SAS），进而可推出AP1=BP1.

显然上述推理适用于点P1不在线段AB上的情形，即两个三角形存在；而当点P1在线段AB上时，点P1与AB的中点C重合，显然有AP1=BP1. 教学中，教师要注意培养学生的推理分析能力，让他们养成严谨思考的习惯.

3. 活动3：语言描述，性质归纳

通常，几何性质可以用文字语言和几何语言来概括，故归纳性质时，教师要引导学生用这两种语言来描述，以提升学生对性质的理解. 基于上述验证，学生可得到如下结论.

几何语言：如图4所示，直线l⊥AB，垂足为C，AC=CB，点P在l 上，则PA=PB.

文字语言：线段垂直平分线上的点到这条线段两个端点的距离相等.

教学中，对于几何结论，为了理解性质、定理，教师要引导学生根据几何结论绘制对应的图像，结合几何条件提取几何特征，由几何结论分析几何性质. 对于文字结论，教师要引导学生关注命题的“题设”与“结论”，对性质定理进行拆解，如对于线段垂直平分线的文字结论，教师可把它拆分成题设与结论，其中题设为一点在线段的垂直平分线上，结论为该点到这条线段两个端点的距离相等. 对于该命题，教师还可以引导学生逆向思考，结合等腰三角形的“三线合一”来推导几何结论.

4. 活动4：性质应用，知识强化

“知识应用”环节有助于强化对性质的理解，故问题设计既要立足于性质定理，又应注重问题变式，于是教师教学时可从两大视角进行引导探究：一是利用逆定理作线段的垂线；二是利用性质定理证明推理.

预设问题1：如图5所示，已知直线AB和直线AB外的一点C，请用圆规和无刻度的直尺作直线AB的垂线，且垂线经过点C.

问题引导：此问题已知直线垂线上的一点，为了得到垂线，需要知道垂线上另一点的位置，故可参考线段垂直平分线的逆定理，即找到直线AB上的两点，且点C到这两点的距离相等，再以这两点构成的线段为底，作任意的等腰三角形. 等腰三角形的另外一个顶点就是所求的垂线上的另一点. 作图痕迹如图6所示.

预设问题2：如图7所示，在△ABE中，D，C两点均在BE上，且AD⊥BE，BD=DC. 若点C在AE的垂直平分线上，试分析AB，AC，CE之间的数量关系，以及AB+BD与DE之间的数量关系.

问题引导：由线段垂直平分线的性质定理可直接推出AC=EC，AB=AC，进而可得到AB=AC=CE. 对于AB+BD与DE之间的数量关系，可由等量代换得AB+BD=CE+CD=DE，即AB+BD= DE.

合理渗透思想，提升综合素养

数学思想是解决问题的重要工具，在几何定理教学中，教师同样要重视数学思想的渗透. 在教学环节合理渗透数学思想，能让学生逐步感知到数学思想，从而提升学科素养. 教学“线段的垂直平分线的性质”时，教师需要重点渗透从特殊到一般、分类讨论和数形结合三大思想.

以“线段的垂直平分线的性质”探究为例，在“推理验证”环节，线段的垂直平分线上的点的选择就可以滲透从特殊到一般的思想，即先设定“特殊性”的定点，再从“一般性”的角度来探索点的位置变化时的结论；在“推理验证”环节可渗透分类讨论思想，培养学生思维的严谨性，即对于线段垂直平分线上的点，可分点在线段上和点不在线段上两种情形，然后分别构建模型进行推理验证；在“知识应用”环节则可以渗透数形结合思想. 特别地，对于数学思想，教师在教学中还要注重解题思路的引导，以下面的问题为例：

如图8所示，在△ABC中，AB的垂直平分线交AB于点E，交BC于点D，连接AD. 已知△ADC的周长为13 cm，AC=5 cm，试求BC的长度.

思想引导：引导时需要分两个过程——以“形”释“数”和由“数”照“形”，即结合图形理解条件，把握图形特征，挖掘几何关系，再由代数推导结论.

在教学环节渗透数学思想，能为新知赋予“思想”特性，有助于学生感悟、理解定理，让学生的思想进一步升华，从而提升综合素养. 不过，数学思想较为抽象，所以教师在教学中要把握其中的精髓，立足知识规律，利用数学思想指导探究，帮助学生积累探究经验.

总之，教学“线段的垂直平分线的性质”时，教师要把握知识核心，以知识探究的方式开展教学探讨，且探究过程围绕“距离相等”全方位构建几何模型，多方式、多角度地进行论证展示. 教学中教师还要关注学生的思维活动，利用引导性问题推进教学，融合知识教学与素养培养，从而提升学生的综合能力.