【摘 要】 针对高中数学概念的抽象性，教师通过深度教学，促使学生深刻理解概念的内涵和外延，牢固掌握概念，灵活运用概念，指引学生从“浅层学习”走向“深度学习”.以沪教版新教材“事件的独立性”为例，阐述基于深度学习如何优化数学概念教学.

【关键词】 深度学习;概念教学;事件的独立性

1 深度学习对高中数学概念教学的意义

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反应形式，是数学知识的“细胞”.《普通高中数学课程标准（2017年版2020年修订）》明确提出：通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验（简称“四基”）;提高从数学角度发现和提出问题的能力、分析和解决问题的能力（简称“四能”）[1].章建跃指出：数学教学的本质是概念教学，让学生养成从基本概念出发思考问题、解决问题的习惯;加强概念的联系性，使学生学会从概念的联系中寻找解题方法[2]. 因此概念教学是学生落实“四基”，提高“四能”的基础，是提升数学思想、发展数学思维、落实核心素养的基石.

“深度学习”是指“学习者能动地参与教学的总称”，即通过学习者能动地学习，培育囊括了认知性、伦理性、社会性能力，以及教养、知识、体验在内的通用能力[3].针对高中大部分数学概念的抽象性，教师通过深度教学，促使学生深刻理解概念的内涵和外延，牢固掌握概念，灵活运用概念，进而学生的学习从“浅层学习”走向“深度学习”.通过教师深度教学，学生深度参与课堂活动，使学生将既有知识与经验链接起来.关注逻辑与推理，发展批判性思维，变被动学习为主动学习，促进核心素养的落实.

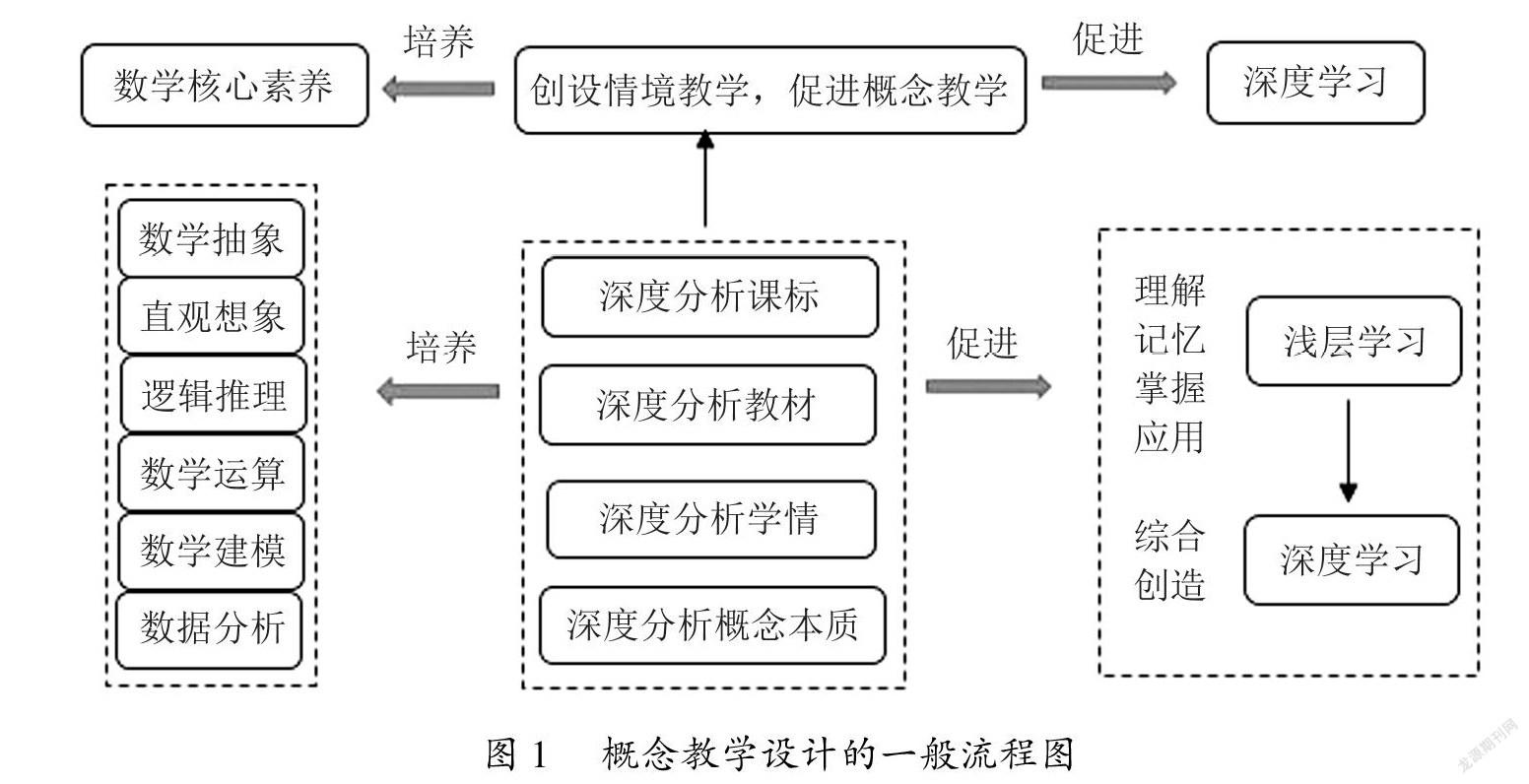
基于高中数学概念的抽象性，教师需要深度研究课标、教材与学情，创设合适的情境，启发学生思考，引导学生把握概念的本质.以下是笔者整理的概念教学设计的一般流程图（见图1），可以为一线教师的实践探索提供有价值的、可参考借鉴的范式.

2 借助情景教学促进数学概念的深度学习

在理论的指导下，结合教学实践，以沪教版新教材中“事件的独立性”为例，阐述如何借助情景优化概念教学，促进深度学习.2.1 教材及学情分析

本节课是沪教版新教材必修三“概率初步”中“随机事件的独立性”的第二课时，主要内容是事件的独立性.本章是概率的初步，借助实际情景，让学生深刻理解如何用数学的眼光观察世界、用数学的语言表达世界、用数学的思维思考世界.本节课在学生掌握了随机现象与样本空间、古典概率、频率与概率的基础上，经历用集合语言表示事件的过程，进一步研究事件的独立性，将直觉与理论紧密结合，逐步理解概率的思想，重视对概率空间的认识，重视数学模型的建立.依据学生的认知特点，遵循从具体到抽象、从特殊到一般的认知规律，借助古典概型定义下的概率，得到相互独立的两个事件的概率与交事件概率间的关系，并为后面条件概率和二项分布的学习奠定基础.

本节课的授课对象是高二美术班学生，他们大部分学习积极努力、态度端正、想象力丰富，但是数学基础比较薄弱，思维方式较固定，对概率的学习有畏惧感，这些都可能对本节课的教学产生影响. 2.2 教学目标

（1）理解事件独立的定义，并能运用两个事件相互独立的充要条件判断两个事件是否独立;

（2）掌握随机事件独立的性质，会利用事件的独立性解决较复杂的概率问题，感受事件的独立性在實际生活中的应用;

（3）通过本节课的学习，渗透分类思想、转化与划归思想，培养学生观察、类比、归纳的能力，提升分析问题和解决问题的能力，发展学生逻辑推理、数学建模、直观想象、数学运算素养.2.3 教学过程2.3.1 情景建模 复习旧知问题1 抛掷甲、乙两枚质地均匀的硬币，用A，B分别表示事件“甲正面朝上”与“乙正面朝上”，试判断：1.事件A与B独立吗？2.试求甲乙都是正面朝上的概率.

师：我准备了两枚硬币，现在请同学甲、乙分别抛掷这两枚硬币，感受事件A与B独立吗？

生1：通过两位同学的演示，可直观感知事件A与B独立.

生2：从概率的角度来看，通过两个事件独立的定义去判断，若P（A∩B）=P（A）P（B），则事件A与B相互独立.P（A）=12，P（B）=12，而P（A∩B）=14，所以事件A与B相互独立.师：大家能否回忆一下我们上节课所学的独立随机事件的定义？

生3：两个事件A与B相互独立是指它们同时发生的概率等于它们各自发生概率的乘积，即P（A∩B）=P（A）P（B）.

师：判断两个事件独立的充要条件是什么？

生4：事件A与B（相互）独立P（A∩B）=P（A）P（B）.

师：回忆如果事件A与B独立，则事件与B什么关系？事件A与呢？事件与呢？

生5：如果事件A与B相互独立，则事件与B相互独立;同理可知事件A与相互独立，事件与相互也独立.

问题2 如果A，B是独立事件，，分别是A，B的对立事件，那么以下等式不一定成立的是（  ）.

A.P（A∩B）=P（A）P（B）B.P（∩B）=P（）P（B）

C.P（A∪B）=P（A）+P（B）D.P（∩）=[1-P（A）][1-P（B）]

生6：如果事件A与B独立，则事件与B独立;事件A与独立，事件与也独立，利用两个事件独立的充要条件即可判断选项A，B，D正确，而选项C是两个事件互斥的性质.设计意图 通过熟悉的独立随机事件，直观感知事件A与B是独立的，而需要严谨的判断，必须通过事件独立的定义，将现实问题转化成数学问题.教师引导，学生复习回忆上节课所学的知识，并通过问题1、2让学生加深理解两个事件独立的充要条件、对立事件的性质、互斥事件的性质、事件独立性的性质.渗透类比思想，提升逻辑推理、数学建模素养.2.3.2 概念辨析 深度研究

例1 判断下列事件A与B是否相互独立？

（1）从一副去掉大小王的52张扑克牌中随机抽取一张牌，用A，B分别表示事件“取得的牌面数是10”与“取得的牌的花色是红桃”;

生7：该题无法直观感知两个事件是否相互独立，只能严格依据事件独立性的充要条件去判断.P（A）=452=113，P（B）=1352=14，而P（A∩B）=152，所以A，B相互独立.

（2）掷一颗骰子，用A，B分别表示事件“结果是偶数”“结果是奇数”;

生8：事件A与B不可能同时发生，P（A∩B）=0，而P（A）=12，P（B）=12，因此P（A∩B）≠P（A）P（B），所以A与B不独立.

问题3 P（A∩B）=0，事件A与B是什么关系？互斥事件与对立事件一样吗？互斥事件与独立事件一样吗？

生9：P（A∩B）=0，所以事件A与B是互斥的.该问题中的事件A与B不仅是互斥事件还是对立事件.互斥事件与对立事件、互斥事件与独立事件是完全不同的概念.

问题4 互斥事件与独立事件在哪些方面不同？

生10：从定义来看：互斥事件是两个不可能同时发生的事件，而独立事件是指事件A是否发生不受事件B的影响;从性质来看：事件A與B互斥，则P（A∪B）=P（A）+P（B），事件A与B相互独立，则P（A∩B）=P（A）P（B）.

（3）掷一颗骰子，事件A表示“结果是2”，事件B表示“结果是有理数”;

生11：P（A）=16，P（B）=1，P（A∩B）=16，则P（A∩B）=P（A）P（B），所以A，B相互独立.问题5 P（B）=1，事件B是什么事件？

众生：事件B为必然事件.

（4）掷一颗骰子，事件A表示“结果是奇数”，事件B表示“结果是虚数”.

生12：P（A）=12，P（B）=0，P（A∩B）=0，则P（A∩B）=P（A）P（B），所以A，B相互独立.

问题6 P（B）=0，事件B是什么事件？

众生：事件B为不可能事件.

问题7 依据上面的两题，能否猜想出必然事件和不可能事件与其他事件的关系？

生13：必然事件Ω和不可能事件与任何事件都是相互独立的.设事件A为任意事件，因为Ω∩A=A，P（Ω）=1，所以P（Ω∩A）=P（A）=1·P（A）=P（Ω）P（A），即事件A与Ω独立，同理可知不可能事件与任何事件也独立.

问题8 你能举出生活中有关事件相互独立的例子吗？

众生讨论，选代表回答.

代表1：学生甲与学生乙能否考上大学相互独立;考生的英语成绩与数学成绩相互独立;学生甲与乙是否迟到相互独立等.设计意图 借助生活中的例子，加强概率与实际生活的联系，以科学的态度评价现实中的事件是否相互独立，设计一连串层层递进的问题，激发学生学习的兴趣与参与度.问题8让学生举出生活中独立性的例子，体会独立性的意义，培养实事求是的科学态度，同时增加学生间的交流合作，感受团队合作的重要性，让学生真正参与到课堂中.2.3.3 概念深化类比推广

问题9 甲、乙两名同学同时做同一个实验，甲成功的概率为0.8，乙成功的概率为0.9，甲和乙之间互不影响，求两人都成功的概率.

问题10 甲、乙、丙三名同学同时做同一个实验，甲成功的概率为0.8，乙成功的概率为0.9，丙成功的概率为0.7，甲、乙、丙之间互不影响. 请尝试猜想三人都成功的概率.

生14：猜想甲、乙、丙三人都成功的概率是0.504.

探究1：两个事件A与B相互独立，则P（A∩B）=P（A）P（B）;如果三个事件A，B，C相互独立，P（A），P（B），P（C）与P（A∩B∩C）是否有关系？如果三个事件A，B，C两两独立，P（A），P（B），P（C）与P（A∩B∩C）是否有关系？

生15：类比事件A与B相互独立P（A∩B）=P（A）P（B），可知如果三个事件A，B，C相互独立，P（A∩B）=P（A）P（B），P（A∩C）=P（A）P（C），P（B∩C）=P（B）P（C），P（A∩B∩C）=P（A）P（B）P（C）.

生16：三个事件两两独立，不一定有P（A∩B∩C）=P（A）P（B）P（C）.

师：两位同学回答的非常棒，设样本空间Ω={1，2，3，4}含有等可能的样本点，A={1，2}，B={1，3}，C={1，4}，我们容易得到P（A∩B）=P（A）P（B），P（A∩C）=P（A）P（C），P（B∩C）=P（B）P（C），但P（A∩B∩C）≠P（A）P（B）P（C）.

探究2：如果n个事件A1，A2…An相互独立，P（A1），P（A2）…P（An）与P（A1∩A2…∩An）是否有关系？

生17：类比推广，如果n个事件A1，A2，…，An（n≥3）相互独立，那么这n个事件同时发生的概率等于每个事件发生的概率的乘积，即P（A1∩A2…∩An）=P（A1）P（A2）…P（An），且上式中任何一个或几个事件Ai换成其对立事件Ai后等式仍然成立.

设计意图 借助熟悉的学习生活中的问题，让学生更加直观感知独立性在现实中的应用.由两个事件的独立性，大胆猜想三个事件相互独立，会有怎样的结论，更进一步猜想，如果n个事件相互独立，会有怎样的结论.通过具体的例子让学生感知三个事件两两独立与三个事件相互独立是完全不同的，鼓励学生大胆想象，积极主动发言，培养他们的逻辑推理能力、语言表达能力，发展学生的发散性思维、创造性思维，同时渗透类比、特殊到一般的思想，提升直观想象、逻辑推理素养.2.3.4 概念应用明确外延

例2 甲、乙两人的罚球投中率分别是p与q，两人各投篮一次，求：

（1）都投中的概率;（2）都没投中的概率;（3）至少一人投中的概率;（4）至多一人投中的概率.

师：设事件A为甲命中，事件B为乙命中，事件C为都命中，事件D为都没命中，事件E为至少一人命中，事件F为至多一人命中，则

生18：P（C）=P（A）P（B）=pq，P（D）=P（）P（）=（1-p）（1-q）;

问题11 事件E包括哪些样本点？事件F包括哪些样本点？

生19：事件E=（∩B）∪（A∩）∪（A∩B），事件F=（∩B）∪

（A∩）∪（∩），而且这些事件互斥，所以满足概率的加法公式.

生20：P（E）=P（∩B）+P（A∩）+P（A∩B）=（1-p）q+p（1-q）+pq.

P（F）=P（∩B）+P（A∩）+P（∩）=（1-p）q+p（1-q）+（1-p）（1-q）.

师：还有其他的解法吗？大家有不同的做法可以通过投影展示出来.

生21（展示）：正难则反，所以可以用事件E，F的对立事件去求解，

=∩，=A∩B.

P（E）=1-P（∩）=1-P（）P（）=1-（1-P）（1-q）;

P（F）=1-P（A∩B）=1-P（A）P（B）=1-pq.

生22（展示）：老师，我还有一种解法，因为“至少一人投中”，所以E=A∪B，“A，B两个事件至少有一个发生”的否定是“A与B都没发生”，即A∪B=∩.

P（E）=P（A∪B）=1-P（A∪B）=1-P（A∩B）=1-（1-P）（1-q）.

师：这位同学的想法非常好，本章通过集合的观点定义了随机事件，将事件与集合相对应，借助已有的集合知识和语言，有利于同学们对概率的理解和掌握.在集合学习时，我们介绍过摩根定律，即A∪B=∩，A∩B=∪，这个定律同样适用于概率论的学习.因为事件的关系就是样本空间相应子集的关系，事件的运算就是相应子集的运算，两者是相互对应的.

例3 A，B两人下棋，每局两人获胜的可能性一样.某一天两人要进行一场三局两胜的比赛，最终胜者获得100元奖金.第一局比赛A胜，后因为有其它要事而终止比赛.试问：怎么分100元奖金才公平？

师：大家讨论一下如何分配奖金比较公平？历史上许多的数学家都考虑过这个问题，比如费马、帕斯卡等，并由此开启了概率论的研究.

代表2：直观感觉应该按四六分，因为感觉三七分不公平.

代表3：按最终获胜的可能性大小比例分配.

师：我们从概率的角度研究怎么分奖金公平？看哪位代表回答的正确.

代表4：将每次比赛A获胜记作事件A，B获胜记作事件B，假设比赛可以继续进行，该试验的样本空间通过枚举法列出：Ω={AAA，AAB，ABA，ABB}，按照古典概型的概率计算公式可知，A最终获胜的概率为34，B最终获胜的概率为14，因此A，B两人应该按3∶1来分.

代表5：在实际比赛中，如果A再赢一局，比赛结束.如果第二局A输，再比第三局，这就不是古典概率模型，但由于比赛各局的胜负之间是独立的，所以可以借助事件的独立性解决.设A表示事件“A最终获胜”，A1表示事件“接下去第一局A胜”;A2表示事件“接下去第二局A胜”，A=A1∪A1∩A2，所以P（A）=P（A1）+PA1∩A2=12+12×12=34.因此A，B两人应该按3∶1来分.

设计意图 通过综合性题目，巩固学生对事件独立性概念的理解.例2中“至多至少问题”，需要学生有分类意识，同时让学生深刻体会正难则反，利用对立事件的计算公式求解，为求解较复杂概率问题提供一个范例.例3解决本章第一节提出的两位法国数学家对赌徒提出的分奖金问题的讨论，是概率论的起源，渗透数学史的学习，学生通过自己的讨论，总结不是古典概型问题如何借助事件的独立性去解决.例题的学习渗透了分类的思想、转化与划归的思想，提升学生逻辑推理、数学建模、数学运算等素养.

2.3.5 课堂练习检测概念掷黑、白两颗骰子.

（1）若用A，B分别表示事件“两颗骰子的点数和为7”与“白色骰子的点数是1”，验证A，B是独立的;

（2）若用A，B分别表示事件“两颗骰子的点数和为7”与“两颗骰子中至少有一颗的点数是1”，验证A，B不是独立的.

设计意图 考查在科学的情境下，学生能否正确判断事件的独立性，及时检测数学概念的掌握情况，提升学生的数学建模、数学运算等素养.2.3.6 深度小结评价学习

本节课学到了哪些知识？用到了哪些数学思想？提升了哪些数学素养？

生23：知识：事件A与B相互独立P（A∩B）=P（A）P（B）;如果事件A与B相互独立，则事件与B相互独立，事件A与相互独立，事件与也相互独立.

思想方法：特殊到一般的思想、分类思想、转化与划归思想等.

核心素养：逻辑推理、数学建模、直观想象、数学运算等.

设计意图 学生独立总结有利于检测是否掌握了本节的知识，是否理解本节课所用到的数学思想方法，有利于对本节知识的整体理解，提升学生归纳总结的能力，让学生在做中学.

3 总结与反思

针对抽象的数学概念教学，教师设置基于学情和教材的问题串启发学生独立思考、合作学习并深入探究，让学生经历数学概念的形成过程，关注学生思维的发展过程.让知识由静态转化成动态，由孤立转化成系统，激活学生对知识的深入理解和深度記忆，激发其深度学习的兴趣，最终提升学生的学科核心素养. 通过实践与研究提炼出概念教学的范式（见图2）.

参考文献

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[2] 江锦志.深度学习视角下概念教学的问题设计研究[D].厦门：集美大学，2021.

[3] 佐藤学等.教育的再定义：教育变革展望丛书（第1卷）[M].东京：岩波书店，2016：216.

[4] 潘超.数学概念深度教学须“五理解”——以人教版“一次函数”为例[J].数学通报，2021，60（04）：2529.

作者简介 徐利花（1986—），女，山西大同人，硕士研究生，中教一级;主要研究数学学科教学.