基于小波AlexNet网络的配电网故障区段定位方法
2022-03-16侯思祖郭威王子奇刘雅婷
侯思祖,郭威,王子奇,刘雅婷
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引 言
随着一流配电网建设逐步推进,电网的拓扑结构日益复杂,馈线分支较多,架空线和电缆线路相互混联,难免会发生各种类型故障,若不能及时处理将会影响电力系统的安全稳定运行[1],快速准确定位故障点位置将有利于故障迅速排除,缩短停电时间,减少人工巡线的工作量[2]。目前,电力系统的故障机理较为复杂,数据规模庞大,现有的故障定位方法难以满足定位准确度的需求[3-4]。
传统的配电网故障定位方法大致分为三种:行波法[5],阻抗法[6]和注入信号法[7]。行波法对设备的采样频率要求较高,行波的波头识别较为困难,线缆混合线路还涉及到波速转换问题[8],且行波信号易受噪声和电压幅值波动等因素的影响。阻抗法通过计算故障回路的阻抗寻找故障点位置,线路的多分支、过渡电阻的大小和系统负荷等因素都会影响该方法的准确性。注入信号法通过检测注入信号的路径和特征完成故障定位,方法原理简单,但是对于间歇性电弧接地故障或高阻接地故障,该方法将会失效,并且所需设备昂贵,注入的信号也会对电网有一定的冲击。文献[9]构建了开关函数及评价函数,将定位问题转换成旅行商问题(Traveling Salesman Problem,TSP),通过改进蚁群算法对配网故障进行全局搜索,在一定程度上提升了故障位置搜索效率,但是容易陷入局部最优。文献[10]根据健全线路与故障线路上故障点上下游三相电流突变量的特征实现配网故障定位,但是该方法不够严谨,当线路末端出现故障或线路发生高阻接地故障,定位方法将会出现误判。文献[11]以故障点上下游导纳随频率变化的关系为基础,通过上下游线路零序电流重心频率的不同特性,完成配网故障定位,但实际中,准确地提取重心频率较为困难,且故障接地相角的大小会影响定位的准确性。文献[12]分析了相电流突变量与相电压突变量的导数相关性,通过故障指示器实现配网故障区段定位,但需要较高精度的电流互感器才能获取相电流的突变量。文献[13]引入分级处理思想,通过人类进化算法完成配网故障定位,但对于复杂电网,该方法的灵活性和实用性降低。文献[14]利用全相位快速傅里叶变换频谱校正提取测量点电压电流的基波有效值和相位信息作为特征向量,通过极限梯度提升法建立故障定位器,实现故障测距,但小电流接地系统发生单相接地故障时,工频电流的有效值变化较小,特别是过渡电阻较大时,基波的故障特征进一步减弱,影响该方法的测距精度。文献[15]利用量测的电压电流相位特征,通过堆栈自编码器(Stacked Auto-Encoder,SAE)进行建模,实现故障测距。文献[16]利用三相电流波形的特征,通过卷积神经网络(Convolution Neural Network,CNN)判断故障区段,但没有充分发挥CNN在图像模式识别领域中的优势,且对于小样本的训练集合,CNN易出现过拟合现象。上述方法多数是凭借该领域的研究经验,分析故障特征与故障位置之间的关系,建立定位模型寻找故障点,容易受到人为因素的影响。
《新一代人工智能发展规划》指出人工智能的发展是重大的战略机遇。将新一代的人工智能引入电网的故障分析与定位已成为一种趋势。深度学习作为新一代人工智能的代表,已在自然语言处理、数据挖掘、语音和图像识别等领域有了卓越的成果。深度学习可以通过数据驱动自主挖掘原始输入向量的有效信息。配电网在不同位置发生故障,各区段的电压电流信号将呈现出不同的工况信息[17]。配电网的故障定位问题本质上是一种分类问题,可以利用深度学习在图像识别中的优势实现故障定位。但配网的电量信号是一维时间序列,不具有图像的性质,不适合直接应用深度学习。可以采用合适的信号处理方法,将电网的电量信号转成具有图像性质的像素矩阵作为深度学习方法的输入。目前,尚未见深度神经网络AlexNet在配电网故障定位方面的应用研究。CNN虽然在图像处理领域被广泛应用[18-19],但其结构的相关参数需要用大量具有标签的样本数据才能得到,并且训练过程从零开始,需要较长的训练时间和较大的计算资源。配电网故障定位的信号训练样本数据集较少,若直接利用卷积神经网络,容易出现过拟合现象,影响故障定位的效果。迁移学习通过利用一个领域学习到的知识对另一个相似领域问题进行建模求解[20]。深度迁移学习可以在小样本数据驱动下完成建模,并且训练的速度和效率都有所提升[21]。因此,可以将深度迁移学习方式引入配电网故障区段定位中。
本文提出一种基于深度网络迁移学习模型的配电网故障区段定位方法。以图像模式识别的方式实现配电网故障区段定位。利用小波包变换(Wavelet Packet Transform,WPT)获取配网各区段电量信号的时频矩阵,通过颜色编码将时频矩阵转成像素矩阵,像素矩阵是一种时频谱图,具有图像性质,能囊括当前系统的工况信息。配网不同位置发生故障,像素矩阵也将包含不同的工况信息。通过微调的AlexNet网络自主提取像素矩阵的特征作为预测变量。将自主提取的预测变量分别输入到学习向量量化(Learning Vector Quantization,LVQ)神经网络、支持向量机(Support Vector Machine,SVM)、朴素贝叶斯分类器(Naive Bayesian Machine,NBC)、极限学习机(Extreme Learning Machine,ELM)和门控循环单元(Gated Recurrent Unit,GRU)。通过混淆矩阵显示配电网故障区段定位结果,确定了AlexNet-GRU模型拥有最佳的识别效果。该方法以数据驱动方式实现配网故障特征自主提取与故障区段定位。
1 电量信号时频信息提取
1.1 WPT分解重构原理
傅里叶变换只能在整个时间轴上积分,利用信号的全局特征得到频域信息,不能描述局部时间段的频域特性[22]。傅里叶变换后,时间变量消失,不能提供信号的时频分析,且傅里叶变换在分析突变或不平稳信号时效果不理想。小波变换(Wavelet Transform,WT)是在克服傅里叶分析缺点的基础上发展出来的,是信号时频分析和处理的强有力工具,拥有数学显微镜的美誉。小波变换通过缩放和平移等运算将原始信号分解为一系列小波系数,这样可以获得原始信号各频率子段的频率特征,实现对信号的多尺度细化分析,在时域和频域均具有良好的局部化特征[23-24],但是小波变换只对每次分解得到的低频近似信号进行分解,而对高频细节信号没有作任何处理,这使得信号的高频特征没有被更好的利用。相比小波变换,小波包变换不但对尺度空间进行了分解,也对小波空间进行了分解。由于配网发生故障后,故障信号中不但含有低频成分,还会含有高频成分。利用小波包变换可以实现对配网故障信号无泄漏、不重叠的全频段正交分解,可以更有效地对电量信号进行时频局部化分析。
选择合适的小波基函数对配网的故障信号进行小波包分解与重构,实现对电量信号的初步处理,小波包的分解和重构表达式分别如式(1)和式(2)所示。
(1)
(2)
其中,p、q和d分别代表低通滤波器系数、高通滤波器系数和小波包分解系数;分解层数用k和l表示;小波包节点标号用j和n表示。
1.2 电量信号的时频信息
因为利用小波包分析信号时,对高频带的分解会导致频带错乱,使各子频带的排列顺序交错,因此对分解出来的结果需要按照频率由低到高的顺序重新排列。文献[25]指出配电网信号瞬时频率主要集中在0~3 kHz,采用db4小波作为小波基函数,对电量信号进行4层小波包分解时效果最佳,可以得到信号最为细致的频谱特征。本文的采样频率设为10 kHz,采用4层分解时,第4层分解结果可以得到16个不同的频率的特征信号,按照中心频率大小进行重排,将0~3 125 Hz部分作为配网信号分析的频带,即取第4层分解结果的前5个子频带进行重构,将各子频带重构的信号作为故障分析的数据矩阵,按照三相电压、三相电流的顺序,从上到下依次排列各信号分解出来的子频带。一个周期的采样点数为200,为了抑制端点效应,删掉每行的前5个采样点和后5个采样点,则此时的时频矩阵的大小为30×190。时频矩阵是通过小波包分解电量信号得到的数据矩阵,并不具有图像的性质。采用MATLAB小波工具箱中的wcodemat函数对时频矩阵E量化编码,可将时频矩阵的数据范围转换到[0, 255]之间。通过量化编码,时频矩阵由数据矩阵变换成具有图像性质的像素矩阵。将每个点的像素值根据大小转为不同的颜色,所得结果如图1所示,其中,每个像素点的像素值代表了经小波包分解得到的数据矩阵的数值大小。时频信息图囊括了电量信号的低频特征和高频特征,并且在不同的区段发生故障,时频信息图也会具有不同的纹理特征和颜色分布。时频信息图蕴含了丰富的配网工况信息,可以作为配网电量信号的标识。但是,仅用肉眼,无法准确地区分这些标识,即无法准确地定位故障区段。通过对小波包分解的结果量化编码,配网的电量信号会以图像形式的呈现,引入深度学习方法,将配网故障区段定位问题转换成图像的智能分类问题。
2 故障区段定位模型
2.1 AlexNet模型
2012年,文献[26]设计了AlexNet神经网络模型,在ImageNet大规模视觉识别挑战大赛上一举夺魁,掀起了深度学习在各个领域应用研究的热潮。AlexNet网络模型本质上是一种卷积神经网络,模型结构如图2所示。从图2可以看出,经典的AlexNet模型包含了五个卷积层,三个池化层,三个全连接层和一个Softmax层。五个卷积层分别采用了96、256、384、384和256个不同大小的卷积核[27]对输入数据执行卷积运算。此外,卷积层1和卷积层2利用了局部响应归一化操作。三个全连接层分别含有4 096、4 096和1 000个神经元。第三个全连接层的神经元个数与样本类别保持一致,其输出作为Softmax激活函数的输入。Softmax激活函数以概率分布的形式确定样本类别。
传统的卷积神经网络,激活函数一般采用饱和非线性函数tanh函数,而AlexNet网络采用线性整流单元(Rectified Linear Unit,ReLu)作为激活函数。相比tanh函数,ReLu函数更符合生物神经元激活机理,能够增强网络的稀疏性,提升模型的训练速度,避免梯度消失情况。AlexNet模型引入了dropout技术,随机抑制了某些神经元,将被抑制神经元的激活值置为0,提升了模型的泛化能力,有效地缓解了过拟合问题。AlexNet网络被提出以后,又出现了许多更深的神经网络,例如GoogleNet、R-CNN和VGG等优秀的网络模型。但是相比其它网络模型,AlexNet网络的模型结构简单,易于训练,耗时短,对图像具有较强的辨识能力[28],适合在工程上应用。
2.2 彩虹编码
对小波包分解电量信号的结果量化编码可以得到像素矩阵。像素矩阵是二维图像,虽然可以直接作为CNN的输入,但是配电网故障定位存在小样本问题,用于训练的故障数据较少,而CNN训练过程需要大量的训练样本。深度迁移学习可以在小样本数据驱动下完成建模,因此本文通过小样本的数据集对AlexNet网络微调,可以避免超参数设置不当等问题。
为了完成配网故障定位任务,需要对经典的AlexNet网络最后一个全连接层的神经元数量进行调整,使其数目与待分类对象类别保持一致。AlexNet网络输入的图像需要放缩到固定大小为227×227×3,对小波包分解结果量化编码后的图像是二维灰度图像,不能直接放缩到227×227×3,但是可以对二维灰度图像进行彩虹编码,生成RGB彩色空间,之后执行放缩。彩虹编码是一种伪彩色变换方法,通过函数关系映射,将图像的灰度值映射到颜色渐变的彩色[29],原理过程如图3所示。其中,f(x,y)表示二维图像点(x,y)处的灰度值;TR、TG、TB代表灰度级-彩色变换的传递函数;R(x,y)、G(x,y)、B(x,y)为RGB三基色的分量值。

图3 灰度级-彩色变换原理
伪彩色编码方式分为线性编码和非线性编码[30],线性编码方式操作简单,但是该编码方式的适应性较低;非线性编码方式虽然有较强的适应性,但是该方法较为复杂,计算量较大。彩虹编码兼合了线性和非线性编码方式的优点,采用了分段线性编码方式。彩虹编码的RGB三基色的变换函数分别如式(3)~式(5)所示:
(3)
(4)
(5)
通过彩虹编码可以将二维的灰度图像转换成拥有RGB颜色空间的三维图像,实现彩色增强。对小波包分解结果量化编码,将所得的像素矩阵通过伪彩色编码升高至三维伪彩色图,后续环节缩放到227×227×3作为AlexNet网络的输入。
2.3 GRU算法
门控循环单元(Gated Recurrent Unit,GRU)是长短时记忆网络(Long Short-Term Memory,LSTM)的新变体[31]。LSTM可以有效地解决传统循环神经网络(Recursive Neural Network,RNN)的梯度消失和梯度爆炸的问题,有坚实的理论基础,但是其模型结构较为复杂,需要遗忘门、输入门和输出门三个门函数参与建模,参量数较多,收敛速度慢。GRU网络简化了LSTM的模型结构,只需要更新门和重置门两个门函数就可以达到LSTM同等功能,削减了LSTM的参数量,节约了运算时间[32-33]。图4为GRU子单元网络结构,其中,t和t-1分别为当前时刻和上一时刻;x和h分别表示输入变量和状态记忆变量;r、z和h′分别为重置门状态、更新门状态和候选隐藏状态;“⊙”和“+”分别表示哈达玛乘积和向量加法运算;σ和tanh为激活函数。
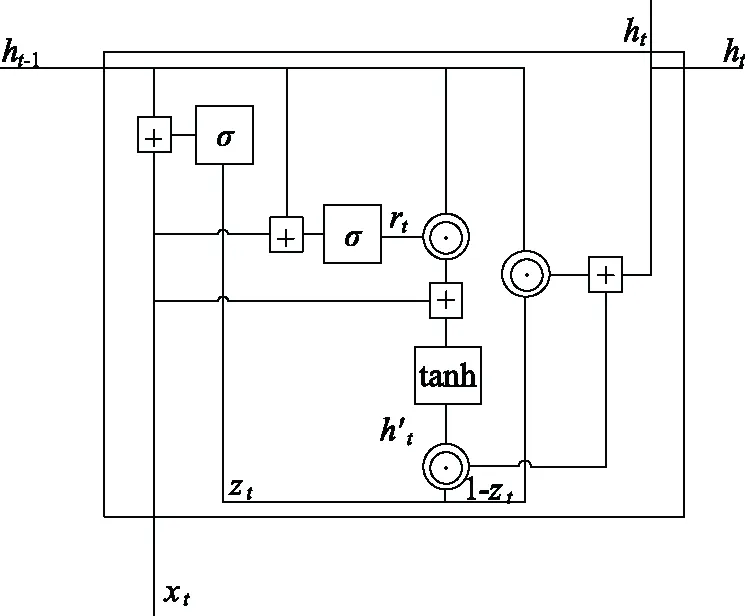
图4 GRU子单元网络结构
3 故障区段定位实现过程
利用小波包变换时频双域的优势,处理配电网的电量信号,通过量化编码将分解结果转成具有图像性质的像素矩阵。像素矩阵囊括了电量信号的时频信息,是一张二维的灰度图像,为适应AlexNet网络输入样本维度227×227×3的要求,采用彩虹编码将灰度图像转成具有RGB颜色空间的三维伪彩色图像。伪彩色图的纹理特征、颜色分布等信息与配网工况密切相关。通过AlexNet网络自主提取伪彩色图中的特征作为预测变量,避免人工提取特征量的繁琐过程,利用模式识别算法对预测变量进行模式识别,即可实现配电网故障区段定位。故障区段定位实现流程如图5所示。
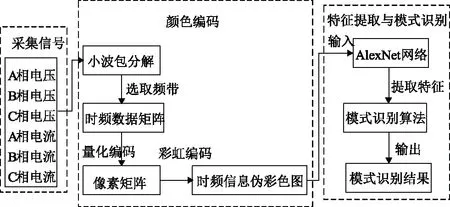
图5 故障区段定位流程
具体实现过程如下:
(1)采集各区段的三相电压和三相电流信号,采样频率为10 kHz,截取故障后一个周期信号数据作为待分解信号;
(2)利用小波包变换对待分解信号进行4层分解,将分解结果按照子频带由低频到高频顺序排列,取第4层小波系数的前5个频带进行重构,获得电量信号的时频矩阵;
(3)对电量信号的时频矩阵进行量化编码,获得像素矩阵,然后,利用彩虹编码对像素矩阵进行升维处理,获得RGB颜色空间的三维伪彩色图像,并将伪彩色图像进行网格规范化压缩处理至227×227×3;
(4)通过微调AlexNet网络提取伪彩色图像的特征,将AlexNet网络第二个全连接层的输出作为特征变量。
将AlexNet网络提取的特征变量送入模式识别算法进行训练,以模式识别的方式完成配电网故障区段定位。其中,模式识别算法的输出为配电网各区段的标签,标签数据采用One-Hot编码形式。
4 实验与分析
4.1 样本配置
基于MATLAB/SIMULINK搭建辐射式中压配电网模型,其拓扑结构如图6所示,通过此模型采集故障样本数据,采样频率为10 kHz。其中,区段1、区段2、区段3、区段4为架空线路,区段5~15为电缆线路。架空线参数:r1=0.178 Ω/km,l1=1.250×10-3H/km,c1=0.061×10-6F/km;r0=0.250 Ω/km,l0=4.560×10-3H/km,c0=0.038×10-6F/km;电缆线路参数:r1=0.278 Ω/km,l1=0.265×10-3H/km,c1=0.438×10-6F/km;r0=2.750 Ω/k,l0=1.118×10-3H/km,c0=0.390×10-6F/km。线路长度为:L1=3 km,L2=2 km,L3=1 km,L4=2 km,L5=4 km,L6=3 km,L7=0.5 km,L8=3 km,L9=3 km,L10=3 km,L11=3 km,L12=3 km,L13=3 km,L14=3 km,L15=1 km。线路的末端负荷均设为0.6+0.3 MV·A。消弧线圈采用过补偿方式,过补偿度设为8%。
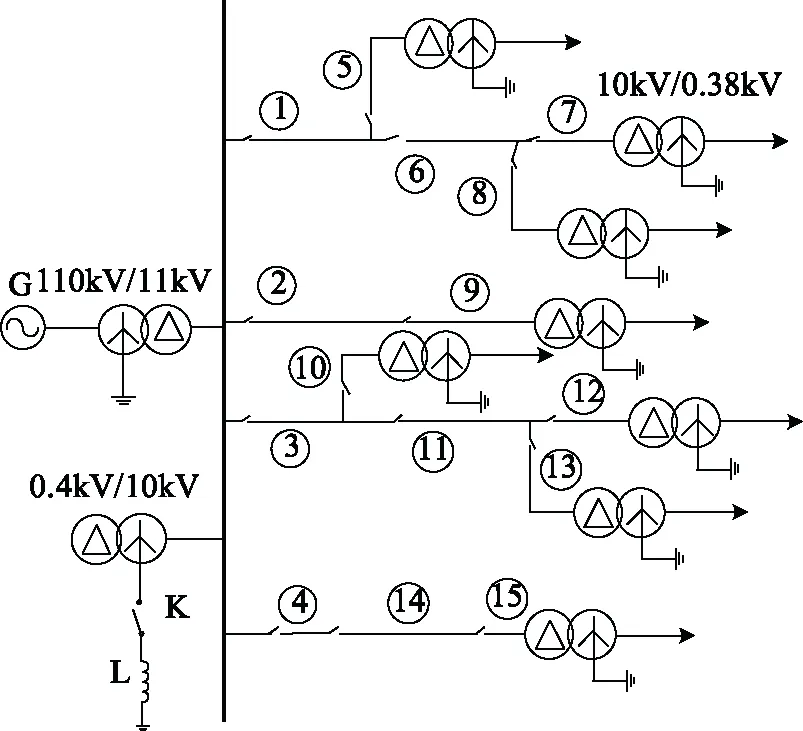
图6 配电网拓扑结构模型示意图
采用文献[12]的区段划分方式将整个配电系统划分成15个区域,采用One-Hot编码形式对15个区域配置标签,所得结果如表1所示。在各区段设置故障点,故障类型包括:单相接地故障(AG/BG/CG)、两相短路故障(AB/AC/BC)、两相接地故障(ABG/ACG/BCG)。故障合闸角包括:0°、30°、60°、90°、120°、150°。单相接地故障的过渡电阻取值区间为0~1 000 Ω,两相接地故障的过渡电阻取值区间为0~10 Ω。

表1 区段编码
对各区段故障后一个周期的三相电压电流信号进行小波包分解,取每个信号的前五个频带重构作为故障分析的数据矩阵。为了抑制端点效应,删掉每行的前5个采样点和后5个采样点,各区段按照三相电压、三相电流的顺序,从上到下依次排列各信号分解出来的子频带。然后,按照区段编号依次拼接到一起,构成该工况下时频矩阵。对时频矩阵进行量化编码和彩虹编码,获得维度为450×190×3的三维时频信息伪彩色图。以区段1,区段2,区段3,区段4发生AG故障为例,电量信号时频信息伪彩色图如图7所示。通过本文提出的故障信号颜色编码方式,可以将配网各区段电量信号融合到一张图像中。不同区段发生故障,图像的纹理参数和颜色分布等特征将会以不同的形式呈现,这些特征会与配网的工况信息密切相关,为实现配电网故障区段定位奠定基础。但是,仅以肉眼,无法准确通过辨识时频信息图确定故障区段,需借助深度学习方法自主完成图像辨识。

图7 电量信号的时频信息伪彩色图
由于整个配电系统被划分成15个区域,需要修改AlexNet网络最后一个全连接层的神经元个数为15,为了加强学习,将权值系数和偏置系数设为20。因此,最终的AlexNet网络各层参数配置如表2所示。

表2 修改的AlexNet网络各层参数配置
图2中,“Valid”表示不扩充边缘;“Same”表示扩充边缘,防止卷积后的图像越来越小。训练网络时,求解器采用Adam优化算法,初始学习效率设为0.000 1,批量大小设置为30,最大训练周期50,每训练100次验证一次。
4.2 特征提取能力验证
为了验证AlexNet网络提取时频信息伪彩色图特征变量的能力,引入传统的CNN网络与其对比。CNN网络包含两层卷积,两层池化。训练样本1 425个,验证样本315个。分别采用Adam和SGDM两种优化器训练传统的CNN网络和AlexNet网络,采用交叉熵作为损失函数。图8为两种模型整体的训练过程。
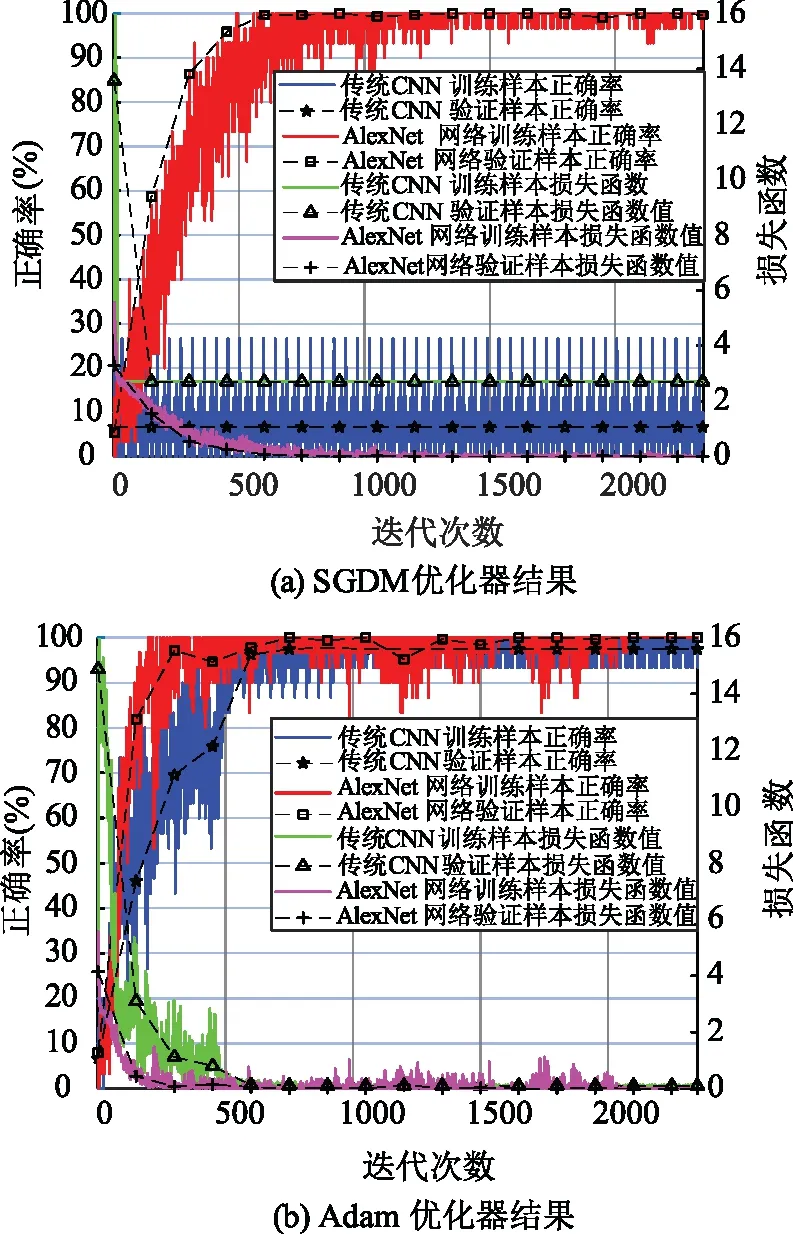
图8 两种模型整体训练过程
从图8(a)可以看出,若采用SGDM优化器,传统的CNN网络的训练样本和验证样本的正确率较低,损失函数函数值较大,说明若采用SGDM优化器,传统的CNN网络已经不具备故障特征提取能力,而AlexNet网络的训练样本正确率逐渐上升,损失函数值逐渐减小,但是结果有所波动。从图8(b)可以看出,采用Adam优化器,传统的CNN网络训练样本的准确率逐渐上升,但是曲线波动较大,且验证样本的准确率低于AlexNet网络验证样本的准确率。当采用Adam优化器时,AlexNet网络的训练样本和验证样本正确率都稳定达到100%,说明网络没有出现过拟合现象,模型训练效果最优,收敛速度最快。
表3列出了两种模型具体参数对比情况,可以看出,AlexNet网络的正确率和训练时间均优于传统的CNN网络,且优化器选择Adam,效果最佳。
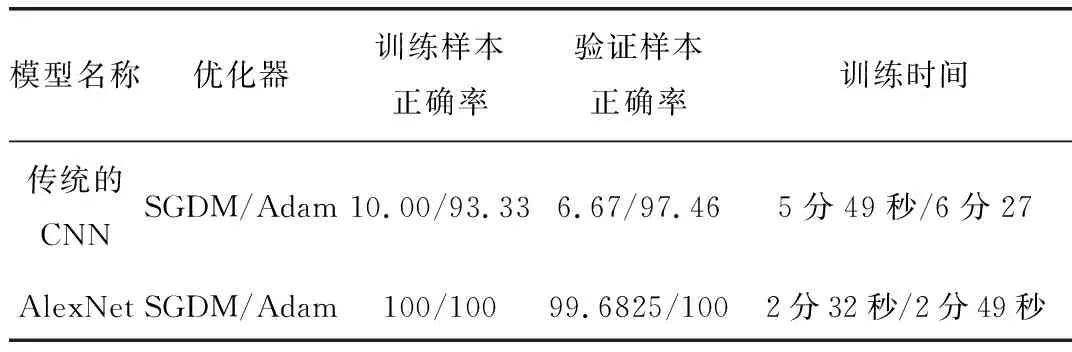
表3 两种模型参数对比情况
为了进一步验证AlexNet网络从时频伪彩色图像中提取特征向量的能力,可以对各层结果进行可视化。由于AlexNet网络每层的输出结果均是一个高维向量,不能直接观察,可以引入流形学习中的t-SNE (t-distributed Stochastic Neighbor Embedding, t-SNE)维数约简算法[34]对高维非线性数据进行降维可视化,图9为输入层和全连接层7特征可视化结果,其中,PC1和PC2分别表示第一主成分和第二主成分。

图9 AlexNet网络特征可视化结果
从图9可以看出,原始各故障区段伪彩色图像的特征相互交叉,难以区分该图像所属类别。经过AlexNet网络的卷积层、池化层等层级的运算,全连接层7输出的特征向量具有较高的辨识度,相同故障区段的特征向量聚集到了一起,不同故障区段的特征区分较为明显。
4.3 不同算法定位结果
用AlexNet网络挖掘训练样本图片和验证样本图片特征,构造时序电量信号高纬度特征向量,作为模式识别算法的训练数据集和验证数据集。
比较常见的模式识别方法,LVQ、NBC、ELM、SVM和GRU。取未参与训练的1 200张电量信号时频信息伪彩色图作为测试样本,采用AlexNet网络自主提取特征,将提取的特征用上述模式识别方式进行分类,通过混淆矩阵对各模式识别方法进行详细的分析,所得结果如图10所示,其中,对角线单元格数值表示正确的区段定位结果,非对角线单元格数值表示错误的区段定位结果。从图10可以看出,相比其它模式识别方法,GRU故障定位效果最好,只出现一个错误判断,准确率可以达到99.92%,分析误判原因,是由于相邻区段被抽取出来的特征较为接近,造成误判。

图10 不同模式识别方法下混淆矩阵实验结果
表4列出了各模式识别正确率、测试时间和测试样本容量,可以看出,ELM模型的测试时间最短,但是区段14发生故障时,识别率仅有82.5%。GRU模型的测试时间仅次ELM模型。但各故障区段识别正确率优于ELM模型。SVM的综合识别正确率与GRU模型较为接近,但是测试时间较长。因此,通过GRU模型识别AlexNet网络提取的特征,实现的配电网故障区段定位效果最佳。
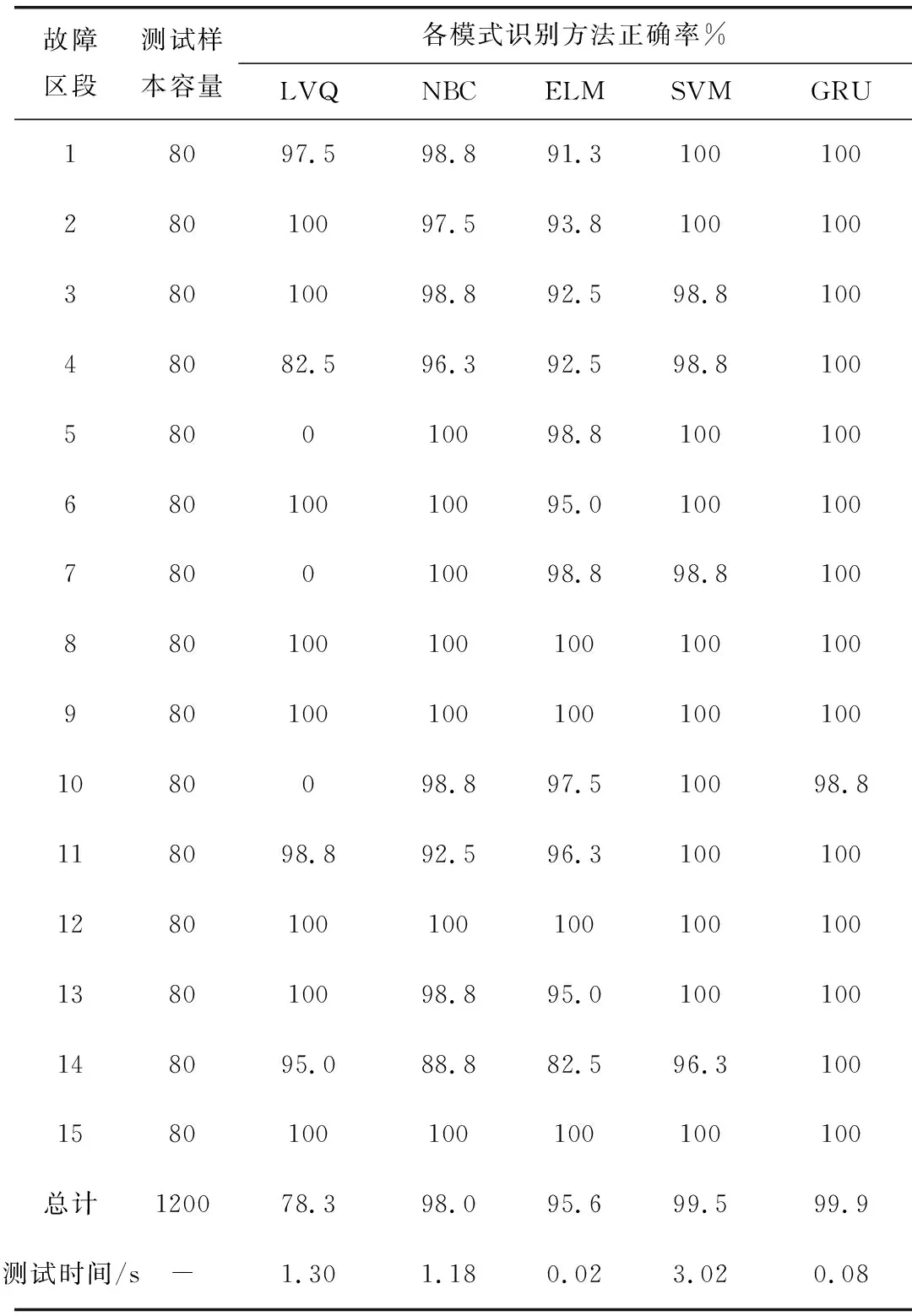
表4 五种模式识别方法的对比
4.4 定位方法的适应性
采集的实际信号或多或少存在噪声,会使原始信号产生畸变,研究配电网故障区段定位在噪声干扰情况下的适应性十分必要[35-37]。在电压电流信号上叠加不同信噪比噪声,表5为故障区段定位结果。从表5可以看出,在电量信号含有信噪比为60 dB~30 dB的噪声时,所提方法依然能准确定位故障区段。可见,文中方法在配电网故障区段定位上有一定的抗噪能力,这是因为小波包分解信号后,选择了0~3 125 Hz部分作为信号分析的频带,削弱了噪声的影响,并且AlexNet网络的卷积与池化运算也有一定的滤波效果。
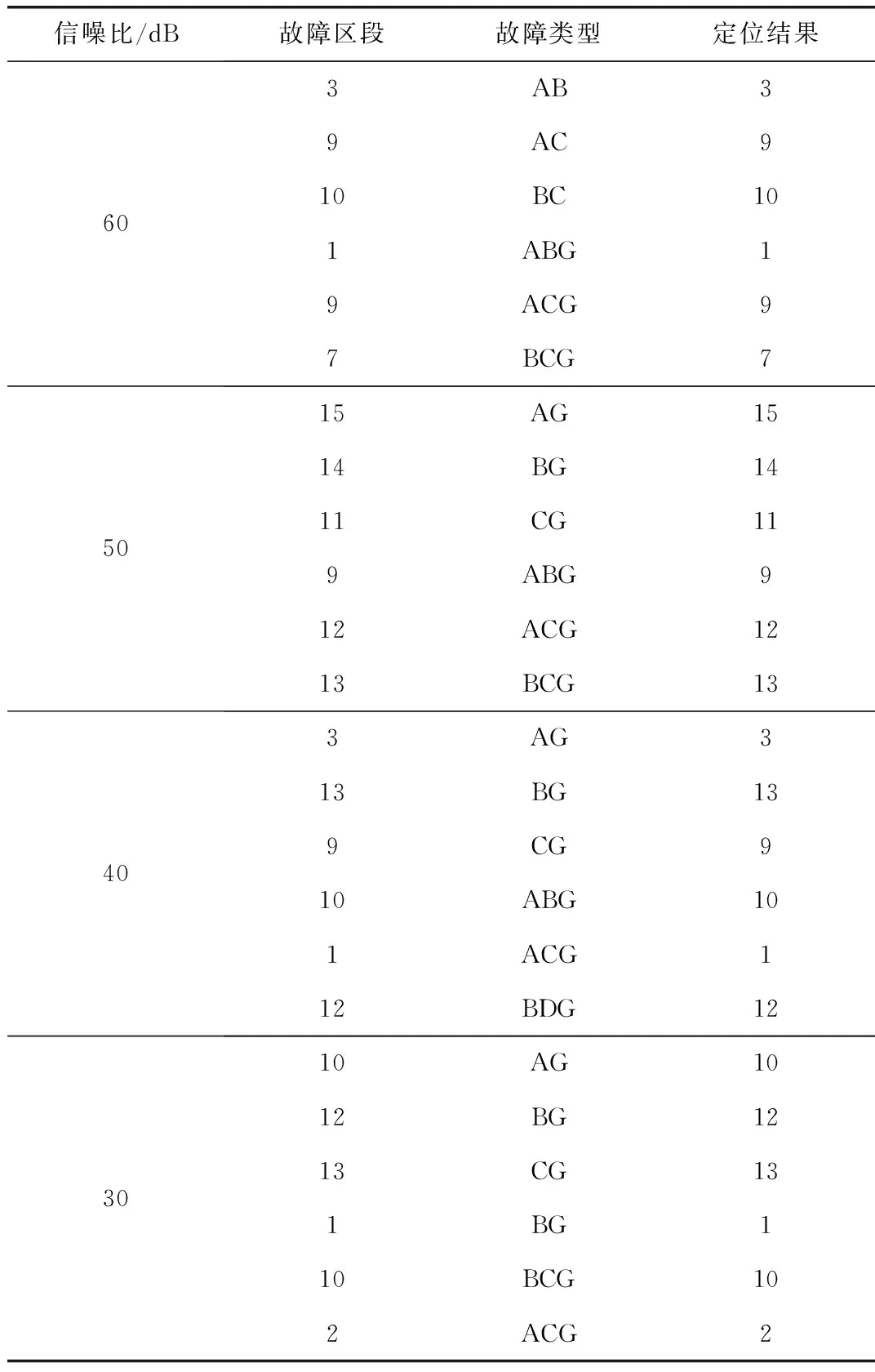
表5 噪声干扰下故障区段定位结果
5 结束语
本文提出一种深度网络迁移学习的配电网故障区段定位方法,以图像模式识别的方式实现故障区段定位,主要工作和结论如下:
(1)利用小波包变换和颜色编码将各区段的电量信号融合到一张含有时频信息的伪彩色图像中。伪彩色图像囊括了丰富的故障信息,其纹理特征、颜色分布等参量和配电网信号的变化有紧密的联系。将电量信号转成图像,可以充分发挥深度学习的优势;
(2)通过AlexNet网络和传统CNN模型对比实验,证明了在自主提取伪彩色图像的高维特征向量方面,AlexNet网络的训练时间和稳定性均优于传统的CNN模型;
(3)相比常见的模式识别方法,利用GRU网络识别AlexNet网络提取的特征,在测试时间和正确率等方面效果最佳;
(4)文中方法利用了深度学习模型结构,可以自主提取故障特征,避免了人为干预,不需要专家经验知识。测试结果表明,所提方法不受故障类型、故障时刻和过渡电阻的影响,并且在噪声干扰和采样时间不同步等方面依然具有良好适应能力。
