广东省佛山市乐从中学(528315) 林国红

一、试题呈现

题目(2020年高考全国Ⅱ卷理科第21 题)已知函数f(x)=sin2xsin 2x.

(1)讨论f(x)在区间(0,π)的单调性;

(2)证明:|f(x)|≤

(3)设n ∈N*,证明:

本题一道以三角函数为背景的函数题.试题结构简单,分步设问,逐步推进,综合考查考生对函数、方程、导数、不等式等基础知识的理解,以及逻辑思维转化、推理论证与运算,以及分析问题和解决问题等方面的能力.

由于问题(1)较为简单,本文不作讨论,下面仅对问题(2),(3)进行解答与探究.

二、试题的解答

1.问题(2)的证明

证法1注意到f(x+π)=sin2(x+π)sin[2(x+π)]=sin2xsin 2x=f(x),故函数f(x)是周期为π的函数.于是可知: 要证明|f(x)|≤只需证明当x ∈[0,π] 时,|f(x)|≤

由问题(1)可知,当x ∈时,f(x)单调递增; 当时,f(x)单调递减;当x ∈时,f(x)单调递增.且有f(0)=f(π)=0,可得[f(x)]max=所以|f(x)|≤

评注本证法先证明函数f(x)是以π周期的周期函数,再借助问题(1)中f(x)的单调性,求得函数的最值,从而证得结论.过程简洁,难点是证明函数f(x)是周期函数.

证法2由|f(x)|=|sin2xsin22x|=|2sin3xcosx|得到

所以|f(x)|≤当且仅当即时,等号成立.

证法3因为

从而sin6xcos2x≤即得|sin3xcosx|≤所以|f(x)|=|sin2xsin22x|=|2sin3xcosx|≤当且仅当时,等号成立.

评注证法2 与证法3 利用四元均值不等式来证明,方法巧妙.均值不等式求最值是高中数学常用方法之一,若要用均值不等式求几个正数积的最大值,关键在于构造条件,使其和为常数,通常要通过乘以或除以常数、拆因式(常常是拆高次的式子)、平方等方式进行构造.

证法4令m ＞0,则

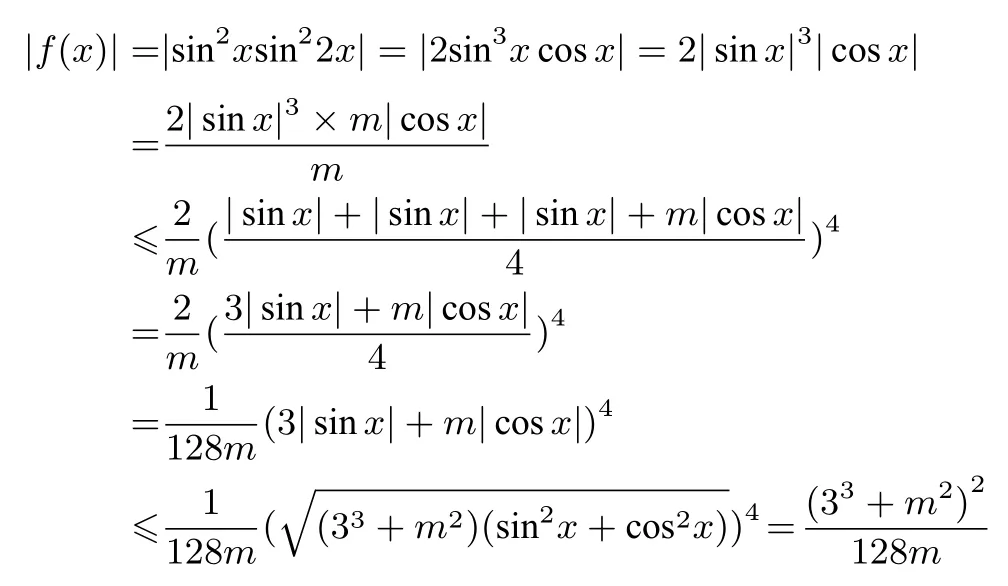
评注本证法利用待定系数法与柯西不等式来证明,引入系数m运用均值不等式后,没有出现和为定值,但是可以再次运用柯西不等式,进而用取等条件计算出待定系数.反之,如果知道取等条件,就可以直接写出系数配凑的过程.

2.问题(3)的证明

由 问 题(2),可 知|f(x)|=|sin2xsin 2x|≤|f(2x)|=|sin22xsin 4x|≤,|f(4x)|=|sin24xsin 8x|≤···,|f(2n-1x)|=|sin22n-1xsin 2nx|≤且由正弦函数的有界性,得|sinx|≤1,|sin22nx|≤1.于是

所以sin2xsin22xsin24x···sin22nx≤

评注问题(3)的证明先利用三角函数的有界性进行放缩,再由问题(2)的结论|f(x)|=|sin2xsin 2x|≤及不等式的基本性质: 同正同向可乘性,来证得题中的不等式.

在本题中,问题(2)可以用问题(1)的结果解答,问题(3)需要用问题(2)的结论,三个问题由浅入深,层层递进.试题的设问意图是为了控制整个试题的难度,实际上是给予考生相应的提示,为考生的解答思路作好铺垫.

三、问题的提出

解答完本题后,思考:

1.若将前述考题的函数f(x)= sin2xsin 2x改为f(x)= sinxsin 2x,则问题(2),(3)是否有最大值? 若有,如何求得?

2.若将前述考题的函数f(x)= sin2xsin 2x改为f(x)= sinxsin22x,则问题(2),(3)是否有最大值? 若有,如何求得?

四、试题的拓展推广

结合原高考题,及对上述两个问题的思考,发现高考试题可以进行推广.经探究,可得到结论1:

结论1已知函数f(x)=sinkxsint2x,k,t,n ∈N*,则有

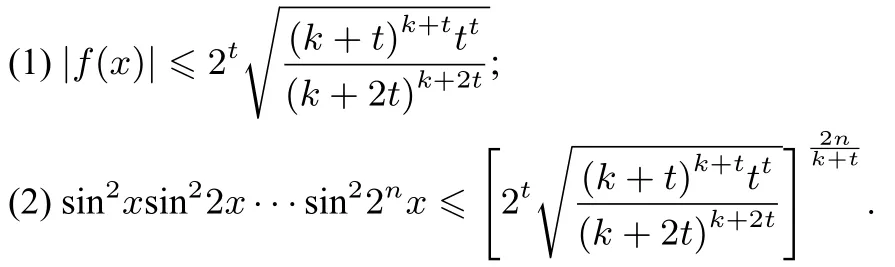
证 明(1)因 为|f(x)|=|sinkxsint2x|=|sinkx(2 sinxcosx)t|=|2tsink+txcostx|,从而

所以|f(x)|≤2t当且仅当时,等号成立.

(2)由(1),可知

···,|f(2n-1x)|=|sink2n-1xsint2nx|≤且由正弦函数的有界性,得|sintx|≤1,|sink2nx|≤1.于是

所以

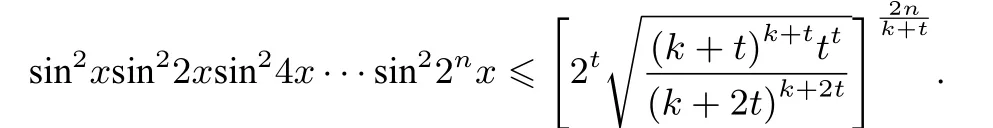
显然,由结论1,当k= 2,t= 1 时,可得|f(x)|≤sin2xsin22xsin24x···sin22nx≤这正是原高考题的情形.

五、试题的类比拓展

类比结论1,经探究,可得到结论2:

结论2已知函数f(x)=coskxcost2x,k,t,n ∈N*,则

证 明(1)因 为f(x)= coskxcost2x= coskx ×(1-2sin2x)t,从而

所以|f(x)|≤当且仅当时,等号成立.

(2)由(1),可知

且由余弦函数的有界性,得|costx|≤1,|cosk2nx|≤1.于是

所以