安徽省太湖中学(246400)李昭平 王 芳

数列求和,是高考考查数列的重点,正所谓常考常新.备考复习中,针对性地梳理数列求和,既能重现数列中的知识,又能突出数列中的思想方法,更能与相关知识沟通联系,起到举一反三、融会贯通的作用.下面结合典型试题,介绍高考中数列求和的七大模型,供参考.

模型1 公式求和法

对于一个整体是等差或等比数列的和式,直接运用等差数列与等比数列的求和公式或它们的性质求和,往往称为公式求和法.解题关键点是:

①确定求和公式中的元素.根据条件确定等差数列求和公式Sn=na1+和等比数列三个求和公式Sn=(q /= 1),Sn=(q /=1),Sn=na1(q=1)中的相关元素,代入公式求和.

②活用等差或等比数列的相关性质.往往已知等差或等比数列中的某些和,要求另外的和,常常运用“Sm,S2m-Sm,S3m-S2m,S4m-S3m,···,也成等差数列”(对等差数列来说)和“当Sm /= 0 时,Sm,S2m-Sm,S3m-S2m,S4m-S3m,··· ,也成等比数列”(对等比数列来说),同时也活用am+an=ap+aq或am·an=ap·aq(m+n=p+q).

例1(2021年高考全国甲卷题)记Sn为等比数列{an}的前n项和.若S2=4,S4=6,则S6=( )

A.7 B.8 C.9 D.10

思路由“S2,S4-S2,S6-S4成等比数列”构建方程求公差t,再求S6,或由S2= 4,S4= 6,利用求和公式构建方程组.

解法1(性质求和)因为Sn为等比数列{an}的前n项和,所以S2,S4-S2,S6-S4成等比数列,所以S2=4,S4-S2=6-4=2,所以S6-S4=1,所以S6=1+S4=1+6=7.故选A.

解法2(求和公式)显然公比q /= 1,由求和公式Sn=得故故选A.

例2(2020年山东青岛模拟考试)若Sn是等差数列{an}的前n项和,S3=-30,S8=-40,则S11的值是____.

思路利用Sn=An2+Bn(A,B为常数),或Sn=na1+或Sn=和am+an=ap+aq(m+n=p+q)处理.

解法1(性质求和)因为{an}是等差数列,所以可设Sn=An2+Bn.由S3=-30,S8=-40 得,故S11= 112-13×11=-22..

解法2(公式求和)由求和公式Sn=na1+得,故S11=11×(-12)+55×2=-22.

解法3(性质求和)因为S8=-40 =a1+a2+a3+a4+a5+a6+a7+a8=-30+5a6,所以a6=-2.故S11==11a6=-22.

模型2 分组求和法

一般地,分组求和法是指对于一个整体是非等差且非等比数列的和式,首先观察它是否能通过适当分组,转化为等差数列或等比数列或常见数列求和.解题关键点是: ①观察结构.观察和式结构特点,看是否能够分成多组数列求和.②实施求和.对每个组分别求和,然后相加,实现整体求和.

例3(2021年福建漳州联考题)在①Sn=n2+n;②a3+a5= 16 且S3+S5= 42;且S7= 56 这三个条件中任选一个补充在下面的问题中,并加以解答.设等差数列{an}的前n项和为Sn,{bn}是等比数列,____,b1=a1,b2=求数列的前n项和Tn.

思路先确定an,再确定bn,最后分组求和得到Tn.

解析若选填条件Sn=n2+n,则等差数列{an}的公差d= 2,a1= 2.于是b1=a1= 2,b2== 4,则其公比q= 2,bn= 2n.因此+2n=+ 2n.故Tn= 1-2n+1--1.若选填条件a3+a5=16 且S3+S5=42,则a1+3d=8 且8a1+13d=42,解得d=2,a1=2.以下过程同上.

注意: 本题属于条件开放性问题,是新课程的亮点.其实质是要确定数列{an},能有效考查思维的批判性、流畅性和深刻性.条件③中的显然与{bn}是等比数列矛盾,不予考虑.只要思考①②即可.

模型3 错位相减求和法

若数列{an}和{bn}分别是等差数列和等比数列,则求其积数列{an·bn}的前n项和,可以运用错位相减法.解题关键点是: ①特殊情形.判断等比数列{bn}的公比是否为1,若为1,直接利用等差数列求和公式求和即可.②一般情形.当等比数列{bn}的公比不为1 时,将和式两边同时乘以这个公比,并跟原和式错位列式、整体相减,转化为等比数列求和,化简整理得到原和式.

例4(2021年高考全国乙卷题)设{an}是首项为1 的等比数列,数列{bn}满足bn=已知a1,3a2,9a3成等差数列.

(1)求{an}和{bn}的通项公式;

(2)记Sn和Tn分别为{an}和{bn}的前n项和.证明:

思路对(1)利用等差数列的性质及a1得到9q2-6q+1 =0,解方程即可;对(2)利用公式法、错位相减法分别求出Sn,Tn,再作差比较即可.

解析(1)因为{an}是首项为1 的等比数列,且a1,3a2,9a3成等差数列,所以6a2=a1+9a3,即6a1q=a1+9a1q2,9q2-6q+ 1 = 0,解得q=所以an=故

(2)由(1)可得Sn=

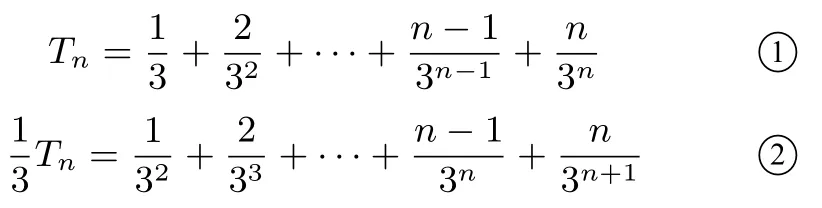
①-②得

例5(2021年高考全国甲卷题)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折,规格为20dm×12dm 的长方形纸,对折1 次共可以得到10dm×12dm,20dm×6dm 两种规格的图形,它们的面积之和S1= 240dm2,对折2 次共可以得到5dm×12dm,10dm×6dm,20dm×3dm 三种规格的图形,它们的面积之和S2=180dm2,以此类推,则对折4 次共可以得到不同规格图形的种数为____;如果对折n次,那么=____dm2.

思路对空1,按对折列举即可; 对空2,根据规律可得Sn,再由错位相减法得出结果,注意乘以分数公比

解析(1)由对折2 次共可以得到5dm×12dm,10dm×6dm,20dm×3dm 三种规格的图形,所以对折三次的结果有:×12,5×6,10×3,20×共4 种不同规格(单位dm2).故对折4 次可得到如下规格:共5 种不同规格.

(2)由于每次对折后的图形的面积都减小为原来的一半,故各次对折后的图形,不论规格如何,其面积成公比为的等比数列,首项为120dm2,第n次对折后的图形面积为120×对于第n次对折后的图形的规格形状种数,根据(1)的过程和结论,猜想为n+1 种(证明从略),故得猜想Sn=

设S=两式作差得,

模型4 裂项相消求和法

无法用公式求和法、分组求和法或错位相减求和法求和的,可以根据和式通项的特点,考虑将其裂项,使得和式中许多项能相消.解题关键点是: ①判断结构.观察一般项的结构,看看它是否可以裂项,能裂项就写出一般项的裂项表达式.②写出和式.按裂项表达式写出和式,看哪些项能相互抵消.③化简整理.计算整理和式,得到和式的最简结果.

例6(2021年安徽合肥六校联考)设数列{an}的前n项和Sn=

(1)求数列{an}的通项公式;(2)若bn=求数列{bn}的前n项和Tn.

思路对(1),只要利用公式an=Sn - Sn-1处理,注意条件n≥2,并对a1进行检验.对(2),由于一般项打破常规,同学们往往不知道对其怎样裂项: 裂成三项没做过,该如何下手未知; 分母是三项积裂成两项也没做过,该怎么凑配未知.绝大部分学生因找不到思路,使解题陷入困境.其实,如果对和)比较熟悉,则能想到视anan+1和an+1an+2为两个整体,即朝的方向裂项.

解析(1)由知,数列{an}是等差数列,所以解得a1= 2,d= 3,故an=3n-1,n ∈N*.

(2)由(1)知,

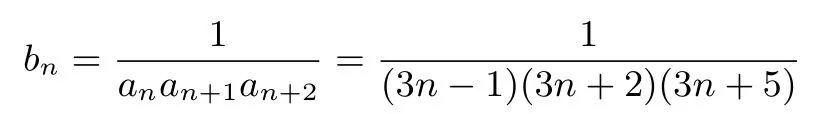
因为(3n+5)-(3n-1)=6,所以

于是

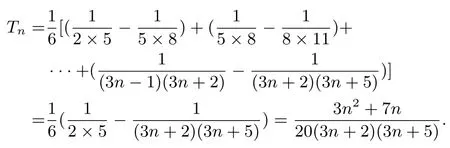
注意: 裂项相消求和法是数列求和的一种重要方法.常见的裂项有:

这给我们很大启发,进一步有

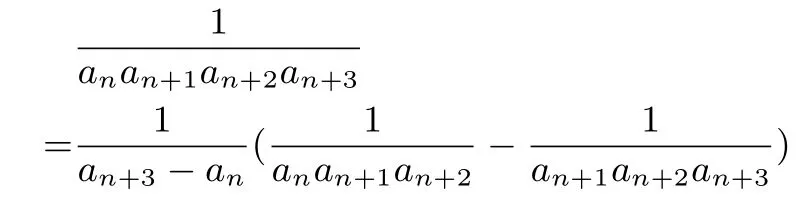
等等,大大拓宽了我们的思维空间和知识视野.正如北大田刚院士所说: 解数学题既要讲原则性和规律性,又要讲灵活性和变通性.这种新的裂项方式就应该是数学方法的灵活性和变通性的体现.

模型5 分类讨论求和法

有些和式中,含有绝对值符号,要分类讨论数列项的正负才能去掉绝对值符号,实现求和.解题关键点是: ①判断项的正负.通过解不等式得到哪些项是正的,哪些项是负的.②去掉绝对值.按项的正负去掉绝对值,分别处理项全正或全负的求和.③讨论项数n的范围.分类讨论项数n的范围,实施整体求和,

例7(2021年湖北武汉段考题)设等比数列{an}的前n项和为Sn,a1=1,S3=13.

(1)求通项公式an; (2)若{an}是递增数列,求数列{|an-n-2|}的前n项和.

思路先确定数列{an}的通项,然后考察an-n-2 的正负.

解析(1)设等比数列{an}的公比为q.由题意得a1+a1q+a1q2=13,即1+q+q2=13,解得q=3 或q=-4.故通项公式an=3n-1,n ∈N*,或an=(-4)n-1,n ∈N*.

(2)由(1)知,an= 3n-1,n ∈N*.令bn=|an-n-2|=3n-1-n-2.由3n-1-n-2 ≥0 知,3n-1≥n+2,所以n≥ 3.由3n-1- n -2＜0 知,n≤ 2 即n= 1,2.设数列{|an-n-2|}的前n项和为Tn=b1+b2+b3+· · ·+bn.当n= 1 时,T1=b1= 2;当n= 2 时,T2=b1+b2= 3; 当n≥ 3 时,Tn=故Tn=

注意: 本题第(2)问,需要去掉绝对值符号来求和,这势必涉及数列{an-n-2}中哪些项是非负的,哪些项是负的.在确定了第3 项开始是非负的条件下,对n= 1,n= 2和n≥3 分类去掉绝对值求和,并涉及到分组求和,最后整合成分段函数的形式.

模型6 并项求和法

有些数列的项与项数的奇偶有关,与正余弦函数的值有关,与数列的周期性有关等等,且其和式无法用熟悉的方法处理,可以考虑恰当并项,使其整体可以转化为熟悉的形式和方法求和,称之为并项求和法.解题关键点是: ①观察结构.观察数列通项与和式的结构特点,选择并项的策略.②审视可能的并项.判断是相邻项并一起,还是间隔项并一起,以整体能求和为标准.③实施整体求和.利用已有的方法,求出和式的最简结果.

例8(2021年四川成都模考题)已知数列{an}的前n项和,且2Sn=an+n2,其中n ∈N*.

(1)求数列{an}的通项公式;(2)设bn=(-1)nan+2n,求数列{bn}的前2n项的和T2n.

思路对(1),利用函数观点赋值处理即可; 对(2),对bn=(-1)nan+2n实施并项求和.

解析(1)当n≥2 时,2Sn-1=an-1+(n-1)2.与2Sn=an+n2相减得,2an=an -an-1+n2-(n-1)2,即an+an-1=2n-1,因此an+1+an=2n+1.两式相减得an+1-an-1=2,所以an=n,n ∈N*.

(2)bn= (-1)nan+ 2n= (-1)n · n+ 2n=于是

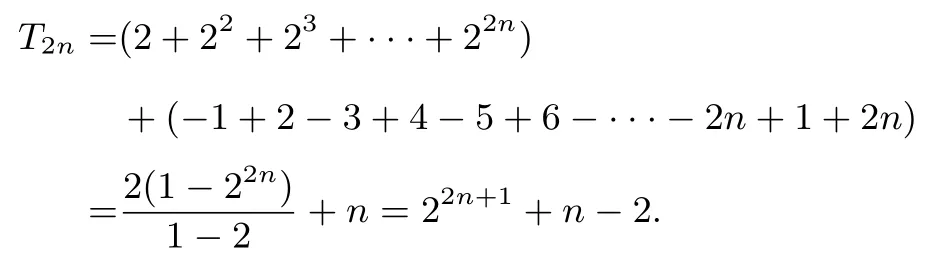
模型7 放缩求和法

证明数列中的不等式,是近年来高考中出现的新热点.其中常常要涉及到求和问题,而这些和又无法用上述6 种模型计算,必须实施放缩变形,转化为熟悉的模型处理,往往称为放缩求和法.解题关键点是: ①观察结构.观察和式的结构特征,确定如何放缩.②恰当放缩求和.对一般项进行放缩,转化为熟悉的模型(等差、等比,可以分组,可以裂项,可以错位相减)求和.③往证不等式.研究新和式中的不等关系,实现证明数列中不等式的目标.

例9(2019年浙江高考题)设等差数列{an}的前n项和为Sn,a3= 4,a4=S3,数列{bn}满足: 对每个n ∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比数列.

(1)求数列{an},{bn}的通项公式;

(2)记cn=n ∈N*.证明:c1+c2+c3+···+cn ＜

思路对(1),利用a3=4 和a4=S3构建方程组求解等差数列{an}的首项和公差,进一步得到Sn,求出bn;对(2),将一般项cn=进行放缩求和,实现目标.

解析(1)设数列{an}的公差为d,由题意得a1+2d=4,a1+ 3d= 3a1+ 3d,解得a1= 0,d= 2.从而an= 2n -2,n ∈N*.由Sn+bn,Sn+1+bn,Sn+2+bn成等比数列得,(Sn+1+bn)2= (Sn+bn)(Sn+2+bn).解得bn=所以bn=n2+n,n ∈N*.

(2)因为

所以

例10(2020年皖西南联盟联考题)在正项数列{an}中,已知a2=

(1)确定数列{an}的单调性,并求{an}中项的最小值;

(2)证明: 对任意n ∈N*,都有an≤成立.

思路对(1),利用数列的单调性即可;对(2),利用放缩求和法处理.

解析(1)因为an+1=an+所以an+1-an=＞0,即数列{an}单调递增.因此{an}中项的最小值是a1.在递推式中,令n=1,则a2=a1+,即解得a1=或a1=(舍去).故a1=

(2)由(1)知,an+1＞an,所以an+1-an=＜,即于是,当n≥2 时,即当n=1时,an=故对任意n ∈N*,都有an≤成立.

注意: 例9 中的cn=无法直接求和式c1+c2+c3+···+cn.先将其放缩成cn ＜利用裂项相消求和法处理.但若放缩成cn ＜则无 法证出c1+c2+c3+· · ·+cn ＜因此如何放缩,需要看待证不等式进行尝试.例10 中的递推式an+1=an+以 常 见 的an+1=an+f(n)为背景,但又跳出了原有模式而设置,给人耳目一新之感.对(2),显然无法求出通项公式{an},只能从递推式中考虑.

由于递推式an+1=an+与以往形式不同,学生往往不知道利用放缩变形解题,知道的也难以对其正确地放缩变形.其实,如果对于和比较熟悉,就可能利用“放缩、裂项、累加”破题.要素是“看目标、看条件、看关系”.

由上可见,解数列求和问题,其关键在于将和式朝着我们熟悉的、已知的模型转化.到底选择哪一种模型,必须根据和式的结构特点,灵活处理,有时候需要多种模型融为一体,共同发挥作用.