秦春

（怀化学院初等教育部，湖南怀化418008）

1 引言

设C为复平面，∏+={z∈C，Im z＞0}为复平面C上的上半平面，H（∏+）为上半平面∏+上的全纯函数全体，S（∏+）为上半平面∏+上的全纯自映射全体.

对任意的0≤p＜∞，定义

称为Hardy空间，易知在范数||g||Hp（∏+）下为Banach空间.

对任意的f∈H（∏+），若满足

则称为n次加权型空间.

当n=0时，称为Bers型空间，记为A∞（∏+）.易知Bers型空间在范数

下为Banach空间.

当n=1时，称为Bloch型空间，记为B（∏+）.Bloch型空间上的函数满足

其中，b（f）为Bloch型空间的半范数.易知Bloch型空间在范数

下为Banach空间.

当n=2时，称为Zygmund型空间，记为Z（∏+）.

Zygmund型空间上的函数满足

其中，bZ（f）为Zygmund型空间的半范数.易知Zygmund型空间在范数

下为Bananch空间.

令φ∈S（∏+），u∈H（∏+），定义H（∏+）上的加权微分复合算子Dnφ，u为：

文[2-7]中研究了单位圆盘上一类解析函数空间上加权微分复合算子的有界性和紧性.Sam Elliott在文[8]中研究了上半平面Hardy空间上复合算子Cφ的有界性.StevoStevic＇在文[9]中研究了上半平面从Hardy空间到Zygmund-型空间复合算子Cφ的有界性.姬小斌，于涛在文[10]中研究了上半平面从经典的Hardy空间到增长型空间及Bloch型空间加权复合算子Dφ，u的有界性.胡清孝、叶善力、刘慧琴在文[11]中研究了上半平面从Hardy空间到增长型空间及Bloch型空间加权复合算子Dφ，u的有界性.其他与上半平面相关的内容见文[12].

2 主要结果

本文研究上半平面从Hardy空间到Bers型空间和Bloch型空间的加权微分复合算子的有界性，结论如下：

定理2.1令n∈N*，u∈H（∏+），φ∈S（∏+），则∶H（p∏+）→A∞（∏+）为有界算子的充分必要条件是

定理2.2令n∈N*，u∈H（∏+），φ∈S（∏+），则∶Hp（∏+）→B（∏+）为有界算子的充分必要条件是

定理2.3令n∈N*，u∈H（∏+），φ∈S（∏+），则Hp（∏+）→Z（∏+）为有界算子的充分必要条件是

3 定理的证明

在证明之前，给出所需的引理.

引理1[9]假设p≥1，n∈N并且w∈∏+，那么

并且

引理2[13]如果f∈Hp（∏+），那么

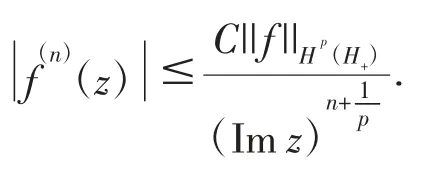
定理2.1的证明：充分性证明.对任意的f∈Hp（∏+），结合（1）式及引理2，可得

固定w∈∏+，任意的p≥1，m∈N，做检验函数

由引理1，可得fw，m（z）∈Hp（∏+）.通过简单的运算，可得

结合（8）式，可得

则（1）式成立.从而定理2.1成立.

定理2.2的证明：充分性证明.对任意的f∈Hp（∏+），结合（2）式、（3）式及引理2，可得

固定z∈∏+，做检测函数

由引理1可知，fz（w）∈Hp（∏+）.结合（9）式并通过简单的运算，可得

可得

结合（12）式，可得

从而（2）式成立，再做检验函数

同理可得（3）式成立.从而定理2.2成立.

定理2.3的证明：充分性的证明.对任意的f∈Hp（∏+），结合（4）式、（5）式、（6）式及引理2，可得

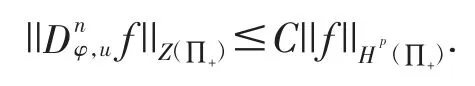
固定Z∈∏+，做检测函数

由引理1可知，fz（w）∈Hp（∏+）.结合（14）式并通过简单的运算，可得

可得

结合（18）式，可得

从而（4）式成立.再做检验函数

同理可得，（5）式和（6）式成立，从而定理2.3成立.