张天舒 李寅龙

摘 要：在集中式与分布式结构基础上建立基于对等式结构的模型， 针对对等式结构下无源定位相对导航的源最优选择问题， 利用高斯-牛顿法设置相对导航卡尔曼滤波器初值使其快速收敛， 定义时间、 位置、 几何、 综合误差因子， 设置不同仿真环境研究距离、 速度、 时间偏差和几何分布位置对相对导航精度的影响。 仿真表明， 偏差与相对导航精度呈反比关系。 当待定位节点与导航源连线夹角为90°时， 导航精度最高， 导航源直线配置时， 宽基线方案的精度要明显优于窄基线方案， 且四源定位的精度优于两源、 三源定位。 本文建立的算法模型能够较好分析不同因素对定位误差的影响。

关键词：对等式结构; 相对导航; 卡尔曼滤波; 初始偏差; 几何分布位置; 雷达信号; 目标跟踪

中图分类号：    TJ765; V294.3   文献标识码：    A 文章编号：1673-5048（2021）04-0043-06

0 引  言

多传感器目标跟踪中常采用集中式与分布式结构。 集中式结构中各节点发送数据至融合中心进行信息融合， 对通信和计算能力提出了较高要求[1]。 分布式结构中各节点独立处理局部观测数据后汇总到融合中心进行处理， 减轻了通信量、 计算量的负担， 且能达到与集中式相近的精度[2]。 集中式与分布式结构都依靠融合中心完成全局态势的信息融合， 但多传感器以及情报源的信息传输可能造成信息爆炸。 在恶劣信息战环境中， 如果融合中心性能瘫痪， 将对作战能力造成毁灭性打击， 因此提出对等式结构以弥补集中式、 分布式结构抗毁性差的缺点。 对等式结构具有无源定位和高精度相对导航的能力， 能够实时截获和锁定节点相对坐标， 间接校正运动节点导航系统的数据， 并传递分享自身导航源数据。 P2P技術、 Ad-Hoc网络、 区块链、 联合战术指挥系统数据链（JTIDS）等， 都是对等式结构的成熟应用[3]。

针对多传感器目标跟踪中相对导航问题， 文献[4]提出RBF辅助的导航算法修正相对导航的精度。 文献[5]利用INS/Link-16的高稳定性与高精度性， 通过测距校正相对导航误差。 在此基础上， 文献[6]利用视觉/INS的参数作为状态变量， 设计EKF滤波器估计相对导航参数。 文献[7]提出覆盖滤波算法， 建立了GPS/INS组合导航的无人机隐蔽干扰算法。 文献[8]建立混合概率模型降低积分误差， 利用视觉与INS的IMU数据进行自主相对导航。 文献[9]利用非线性开普勒模型对卫星的观测能力进行评估分析， 提出了分布式卫星相对导航算法。 文献[10]基于伪距和超宽带的特征， 设计相对导航状态方程对相对状态进行估计。 文献[11]提出LM-IEKF算法解决无人机与非合作目标相对导航的问题。

上述算法从惯性导航、 卫星导航、 无人机辅助导航等方面提出相对导航算法， 但有以下缺点： （1）惯性导航的误差易累积， 需要不断进行修正; （2）卫星导航在恶劣电磁环境下无法建立良好通信; （3）编队运动模型较为单一; （4）皆为给定导航源， 并未考虑在导航源较多情况下该如何选择最优源; （5）考虑了距离、 时间对导航的影响， 但未考虑几何位置的影响， 没有对相对导航源选择的问题进行最优考虑。 本文算法建立在对等式结构下， 增强了节点间的相互联系， 打破分布式结构中各节点相互孤立的局面， 感知覆盖范围广、 灵活性强、 具有实时性， 建立可快速收敛的相对导航滤波器， 并且从时间、 距离、 几何分布等方面分析如何进行最优导航源选择。 在态势瞬变的现代电子战中， 若遭遇电磁静默、 GPS失灵等情况时， 不仅可以更正节点实时位置情报，  更健

全了辅助监视态势的编制， 使对等式信息池中对跟踪/关联目标的信息交换更可靠， 提高作战能力上限， 更适应复杂电磁环境并且提高对全局态势感知的掌握。

1 模型建立

对等式结构实质上是一种分布式、 去中心化的通信模式。 各节点具有同等的地位， 可以互相通信、 共享资源、 协同工作。 节点间交换信息联结成巨大的信息池， 各节点可有选择地从中获取所需信息。 对等式结构中待定位节点可利用TOA（信号到达时间）解算自身与其他源的距离， 并根据导航源发送的位置信息通过多边测距完成相对导航定位[12]。

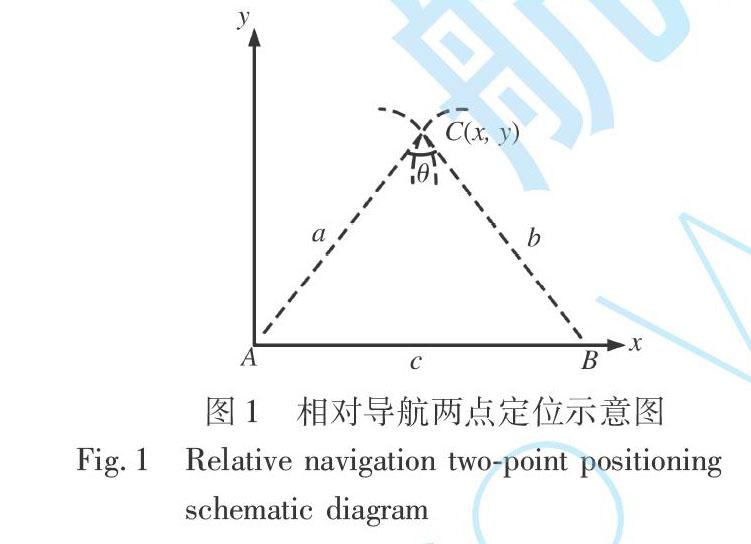
由于系统的导航半径远大于工作高度， 忽略高度影响， 将相对导航建立在二维坐标系下， 如图1所示。 以两点定位相对导航为例， 节点A， B为相对坐标系中固定节点， 相距为c， 节点C通过TOA测算距离a， b， 又在固定时隙接收到节点A， B的位置坐标完成相对坐标系中的定位。

2 算法步骤

2.1 卡尔曼滤波

假设相对导航选择i点定位算法， 建立误差公式：

φi（x， y）=（xi-x）2+（yi-y）2-Ri （1）

式中： （xi， yi）为其他源的坐标; （x， y）为待定位节点坐标; Ri为待定位节点对各源的TOA测距。

利用高斯-牛顿法计算minφi， 以保证卡尔曼滤波持续收敛， 解算偏导如下[13]：

A=x1-xd1…xi-xdiy1-yd1…yi-ydi （2）

φ=φ1（x， y）φi（x， y） （3）

设待定位节点坐标某一初值X0=（x0， y0）， 则有

X1=X0-A（X0）AT（X0）-1A（X0）φ（X0） （4）

不断迭代直至|XK+1-XK|<δ， δ为设定的阈值， 此时确定的初值使卡尔曼滤波快速收敛， 能够迅速达到理想精度。

建立卡尔曼滤波的观测方程如下：

R0=Rc-tac+ε

Rc=（Xt-X）2+（Yt-Y）2 （5）

式中： R0为节点C利用TOA计算的距离值; c为光速; Rc为利用相对坐标计算的距离值; Xt， Yt为其他源发送的位置坐标; X， Y为节点C位置坐标; ta为节点C相对系统时的偏差; ε为量测噪声。

建立观测矩阵为

C=-c0X-XtRcY-YtRc00 （6）

设状态向量为

S=tfXYvxvy （7）

式中： t为相对时间偏差; f为相对时间偏差率; X， Y为节点在相对坐标系中x，  y方向的坐标; vx， vy为节点速度在x，  y方向的分量。

建立状态转移矩阵为

A=1t

1

1t

1t

1

1

（8）

建立噪声扰动矩阵为

Γ=1

1

t

t

t

1 （9）

2.2 定位误差计算

如图1所示， 假设节点A处于相对坐标系原点， 节点B处于坐标（cB， 0）处， 节点C选择节点A， B作为相对导航源， 此时处于相对坐标系的（x， y）处， 通过TOA计算得

a=（t2-t1）cB+ε1 （10）

b=（t4-t3）cB+ε2 （11）

式中： a， b为节点C与节点A， B的距离; t2， t4为节点C向节点A， B发送信号的时间; t1， t3为信号到达时间; ε1， ε2为随机误差。

通过平面几何知识求得

x=a2 + c2B-b22cB （12）

y=2a2b2 + 2a2c2B + 2b2c2B-a4-b4-c4B2cB  （13）

由于x， y與a， b不是线性关系， 将非线性函数用泰勒级数展开， 取零次项和一次项化为线性函数y=fx+f0的形式， 此时有[14]

Dy=E[（fx-fμx）（fx-fμx）′]=

E[f（x-μx）（x-μx）′f′]=

fE[（x-μx）（x-μx）′]f′=fDxf′（14）

假设a， b的误差服从高斯分布且相互独立， 则x， y的误差模型为

Dx=xa2δ2a+ xb2δ2b=a2c2Bδ2a+ b2c2Bδ2b（15）

Dy=ya2δ2a+yb2δ2b=a2b4+a2c4B+a6+2a2b2c2B-2a4b2-2a4c2Bc2B（2a2b2+2b2c2B+2a2c2B-a4-b4-c4B）δ2a+a4b2+b2c4B+b6+2a2b2c2B-2a2b4-2b4c2Bc2B（2a2b2+2b2c2B+2a2c2B-a4-b4-c4B）δ2b（16）

则C点坐标位置方差为

DC=Dx+Dy （17）

源几何分布位置影响着相对导航的精度， 假设节点C位于节点A， B中轴线的垂线上， 分析此时夹角θ对源位置质量的影响。 此时a=b， 设a=b=kcB， 为简化计算， 假设此时δ2a=δ2b=δ2， 则式（17）化简为

DC=8k44k2-1δ2 （18）

将k=12csc（θ2）代入式（18）， 化简为

DC=2csc2θ×δ2 （19）

2.3 误差因子

2.3.1 时间及位置误差因子

定义时间误差因子为

Qt=bi（k， k-1）+Pi（k， k-1） （20）

式中： bi（k， k-1）为第i个导航源在k时刻对时间偏差的估计值; Pi（k， k-1）为卡尔曼滤波噪声协方差矩阵在k时刻主对角线上第i个元素。

定义位置误差因子为

Qp=πxa2δ2a+xb2δ2bya2δ2a+

yb2δ2b=πDxDy（21）

实质上， 位置误差因子是以Dx， Dy为长短轴的定位误差等概率椭圆的面积作为衡量位置质量的标准。

2.3.2 几何误差因子

几何误差要综合考虑导航源的位置分布， 假设待定位节点真实坐标为（xw， yw）， 待定位节点滤波坐标为（x^w，  y^w）， 导航源坐标为（xi， yi）， i=1， 2， …， n， 定位误差为（Δxw， Δyw）， 则有

xw=x^w+Δxw

yw=y^w+Δyw（22）

待定位节点与导航源的真实距离为

ρi=（xw-xi）2+（yw-yi）2（23）

待定位节点与导航源的滤波距离为

i=（x^w-xi）2+（y^w-yi）2（24）

根据式（22）～（24）， 将（x^w，  y^w）利用泰勒级数展开， 只保留一阶偏导数， 可得

Δ ρ=i-ρi=xi-x^wRΔxw+yi-y^wRΔyw（25）

R=（x^w-xi）2+（y^w-yi）2（26）

将式（25）化简得

Δ ρ=HΔ x（27）

式中：

Δ ρ=Δ ρ1Δ ρn，  H=x1-x^wRy1-y^wR

xn-x^wRyn-y^wR， Δ x=Δ xwΔ yw。

利用最小二乘法解算定位误差可得

Δ x=（HTH）-1HTΔ ρ（28）

设G=（HTH）-1， 则定义几何误差因子为

Qg=G11+G22（29）

定义综合误差因子为

Q=W1（Qt+Qp）+W2Qg（30）

综合误差因子是上述三种误差因子的加权因子， 其中W1， W2为加权系数。

时间、 位置质量因子只需单独判断各个源即可， 但考虑几何质量因子时， 需考虑各个源与待定位节点的位置分布情况。

3 仿真结果

3.1 仿真环境

在对等式结构中存在A， B， C三个节点， 节点C选择节点A， B作为相对导航定位源。 节点C运动速度随机在300 ～700 m/s之间， 在0～2π之间随机选取某一角度做匀速直线运动。

仿真环境1： 节点B的位置坐标在x， y方向分别包含从0 m递增到300 m的误差。

仿真环境2： 节点C在x， y方向速度误差分别从0 m/s递增到100 m/s， 由惯性导航误差累积引起的速度漂移服从标准差为0.01 m/s的高斯分布。

仿真环境3： 节点A的时间偏差从10 ns、 100 ns、 300 ns增长到500 ns， 时钟的时间游走噪声服从标准差为10-10 s的高斯分布。

仿真环境4： 节点A， B， C的距离偏差服从均值为10 m、 标准差为100 m的高斯分布， 速度偏差服从均值为10 m/s、 标准差为10 m/s的高斯分布。

仿真环境5： 假设存在编队节点A～G， 以节点A为原点建立相对坐标系， 各节点飞行位置参数如表1所示， 各节点飞行编队模型如图2所示。

3.2 仿真分析

3.2.1 距离偏差对相对导航的影响

如图3所示， 在仿真环境1的条件下， 节点B的位置坐标中含有x， y方向的距离偏差， 距离偏差以50 m为步长， 从0 m递增到300 m， 此时， 节点C滤波解算出相对导航系中与节点B的相对距离值应是定值， 但距离值随着初始距离偏差的增加而增加， 说明导航误差不断增大， 并且两者呈近似线性关系。

3.2.2 速度偏差对相对导航的影响

如图4所示，  在仿真环境2的条件下，  节点C由于惯性导航累积误差在x， y方向上产生从0 m/s递增到100 m/s的速度误差， 速度误差影响卡尔曼滤波精度。 此时， 卡尔曼滤波解算的相对导航距离随着速度误差的增加而增加， 且相比距离偏差， 误差增长的趋势越来越快。

3.2.3 时间偏差对相对导航的影响

如表2所示， 在仿真环境3的条件下， 节点A的时间偏差从10 ns， 100 ns， 300 ns增长到500 ns， 数据产生时间异步， 对解算出x， y方向的距离造成误差。 在时间偏差不超过100 ns时， 仍得到高精度位置解。 在时间偏差不超过300 ns时， 仍得到收敛的位置解， 随着时间偏差的增大， 距离误差不断增大， 两者呈正比关系。

3.2.4 几何分布位置对相对导航的影响

在仿真环境4的条件下， 假设节点C位于图5所示相对坐标系的（0， 100 km）处开始做水平往返运动， 节点A， B从原点出发， 同速度向相反方向运动至100 km处， 图6所示为节点A， B在x轴移动距离与节点C位置方差的三维图像。 仿真表明， 当节点A， B与原点距离低于30 km时， 节点C位置方差极大， 超出30 km后节点C位置方差逐渐下降。 在节点A， B距原点位置均为100 km时， 位置方差达到最低值， 此时节点C与节点A， B连线的夹角为90°， 符合式（19）的理论预期。

假设节点A， B固定于相对坐标系的（-100 km， 0）和（100 km， 0）处， 节点C从（0， 10 km）处出发沿y轴逐渐向上移动， 仿真节点C的x， y方向误差与移动距离的关系如图7所示， 随着移动距离的不断增长， 节点C的y方向误差逐渐增加， x方向误差逐渐减小。 在移动距离为100 km时， x， y方向误差相等， 此时节点C与节点A， B的连线夹角为90°。 若节点C并不处于节点A， B连线的中垂线上， 当连线夹角小于90°时， 径向误差是节点C位置误差的主要来源， 反之， 切向误差为位置误差的主要来源。

仿真环境5条件下， 以节点B， D， E， G作为导航源， 假设节点A， C， F所在直线为相对导航坐标系的y轴， 仿真得到几何误差因子如图8所示。 随着y轴坐标的逐渐增加， 几何误差因子先减小后增加， 在坐标约-2 800 m处预计取得最小值。 当y轴坐标超过2 000 m时， 误差因子上涨较快， 在实际编队中可限制待定位节点位置以提升导航精度。

仿真环境5条件下， 仿真不同导航源数量对几何误差因子的影响如图9所示。 导航源（2）表示导航源为节点B， D; 导航源（3）表示导航源为节点A， E， G; 导航源（4）表示导航源为节点B， D， E， G。 随着待定位节点在y轴位置的逐渐增加， 几何误差因子先减小后增加， 且各情况中取得最低几何误差因子的y轴位置并不相同。 仿真结果表明， 四源定位的精度优于两源、 三源定位。

不同导航源配置方案如表3所示， 各方案下几何误差因子如表4所示。 在三导航源按照直线配置时， 宽基线配置的导航精度相比窄基线配置有明显提升。 在三导航源按照三角形配置时， 导航精度明显优于直线配置， 其中等边三角形配置的导航精度相比等腰三角形配置稍高， 两者相差很小。 导航源数量为4时， 精度优于三导航源配置， 且Y型配置相比菱形配置的导航精度高。

4 结 束 语

针对对等结构下相对导航最优源选择问题， 本文设计了相对导航6状态卡尔曼滤波器， 并且利用高斯-牛顿法设定滤波器初值使其快速收敛。 对影响相对导航定位精度的距离、 速度、 时间偏差以及几何分布位置等因素进行仿真， 设置了5种仿真环境。 仿真表明， 随着距离、 速度、 时间偏差的增加， 距离误差不断增大， 相对导航精度逐渐降低。 分析几何分布位置对导航的影响， 仿真表明， 当待定位节点与导航源连线夹角为90°时， 方差最小; 当夹角小于90°时， 径向误差是定位誤差的主要来源; 当夹角大于90°时， 切向误差是定位误差的主要来源。 导航源直线配置时， 宽基线方案的精度要明显优于窄基线方案， 且四源定位的精度优于两源、 三源定位。

参考文献：

[1] Subedi S，  Zhang Y D，  Amin M G，  et al. Cramer-Rao Type Bounds for Sparsity-Aware Multi-Sensor Multi-Target Tracking[J]. Signal Processing，  2018，  145：  68-77.

[2] Ge Q B，  Wei Z L，  Cheng T F，  et al. Flexible Fusion Structure-Based Performance Optimization Learning for Multisensor Target Tracking[J]. Sensors，  2017，  17（5）： 1045-1050.

[3] Khamayseh Y，  Yassein M B，  Abu-Jazoh M. Intelligent Black Hole Detection in Mobile AdHoc Networks[J]. International Journal of Electrical and Computer Engineering （IJECE），  2019，  9（3）：  1968-1977.

[4] 孙瑶洁，  熊智，  李文龙，  等. 基于RBF神经网络的相对导航信息融合方法[J]. 航空计算技术，  2019，  49（6）：  27-32.

Sun Yaojie，  Xiong Zhi，  Li Wenlong，  et al. Relative Navigation Information Fusion Method Based on RBF Neural Network[J]. Aeronautical Computing Technique，  2019，  49（6）：  27-32. （in Chinese）

[5] 郝菁，  蔚保国，  何成龙. 基于惯导/数据链的动态相对定位方法[J]. 计算机测量与控制，  2018，  26（10）：  191-195.

Hao Jing，  Yu Baoguo，  He Chenglong. Dynamic Relative Positioning Method Based on Inertial Navigation and Data Link[J]. Computer Measurement & Control，  2018，  26（10）：  191-195. （in Chinese）

[6] 张世杰，  宁明峰，  陈健. 非合作目标视觉/惯导相对导航及敏感器自标定方法[J]. 国防科技大学学报，  2019， 41（6）： 25-32.

Zhang Shijie，  Ning Mingfeng，  Chen Jian. Method of Vision/Inertial Relative Navigation for Non-Cooperative Target and Sensors Self-Calibration[J]. Journal of National University of Defense Technology，  2019， 41 （6）：  25-32. （in Chinese）

[7] Guo Y，  Wu M P，  Tang K H，  et al. Covert Spoofing Algorithm of UAV Based on GPS/INS-Integrated Navigation[J]. IEEE Transactions on Vehicular Technology，  2019，  68（7）：  6557-6564.

[8] Liu W L，  Wu S T，  Wen Y M，  et al. Integrated Autonomous Relative Navigation Method Based on Vision and IMU Data Fusion[J]. IEEE Access，  2020，  8（99）： 51114-51128.

[9] Su Q Y，  Huang Y. Observability Analysis and Navigation Algorithm for Distributed Satellites System Using Relative Range Measurements[J]. Journal of Systems Science and Complexity，  2018，  31（5）：  1206-1226.

[10] 熊骏，  熊智，  于永军，  等. 超寬带测距辅助的无人机近距离相对导航方法[J]. 中国惯性技术学报，  2018，  26（3）：  346-351.

Xiong Jun，  Xiong Zhi，  Yu Yongjun，  et al. Close Relative Navigation Algorithm for Unmanned Aerial Vehicle Aided by UWB Relative Measurement[J]. Journal of Chinese Inertial Technology，  2018，  26（3）：  346-351.（in Chinese）

[11] 朱云峰，  孙永荣，  赵伟，  等. 包含乘性噪声自适应修正的非合作目标相对导航算法[J]. 航空学报，  2019，  40（7）：  240-250.

Zhu Yunfeng，  Sun Yongrong，  Zhao Wei，  et al. Relative Navigation Algorithm for Non-Cooperative Target with Adaptive Modification of Multiplicative Noise[J]. Acta Aeronautica et Astronautica Sinica，  2019，  40（7）：  240-250.（in Chinese）

[12] 劉骏，  田福庆，  孙世岩. JTIDS中时差导航定位方法与性能分析[J]. 弹箭与制导学报，  2006，  26（2）：  659-661.

Liu Jun，  Tian Fuqing，  Sun Shiyan. The Navigation by Time-Difference-of-Arrival and Performance Analysis in JTIDS[J]. Journal of Projectiles，  Rockets，  Missiles and Guidance，  2006，  26（2）：  659-661.（in Chinese）

[13] 武楠，  王华，  匡镜明. JTIDS相对导航性能分析和仿真[J]. 系统工程与电子技术，  2005，  27（3）：  464-466.

Wu Nan，  Wang Hua，  Kuang Jingming. Performance Analysis and Simulation of JTIDS Relative Navigation[J]. Systems Engineering and Electronics，  2005，  27（3）：  464-466.（in Chinese）

[14] 曹可劲，  朱银兵，  崔国恒. 基于几何位置的JTIDS定位误差建模与分析[J]. 海军工程大学学报，  2010，  22（3）：  97-101.

Cao Kejin，  Zhu Yinbing，  Cui Guoheng. Error Modeling and Analy-sis of JTIDS Based on Geometrical Position[J]. Journal of Naval University of Engineering，  2010，  22（3）：  97-101.（in Chinese）

Research on Relative Navigation Source Selection in

Peer-to-Peer Structure

Zhang Tianshu ， Li Yinlong

（Naval Aviation University，  Yantai 264001， China）

Abstract：  On the basis of centralized structure and distributed structure，  the model based on peer-to-peer structure is established. Aimed in the problem of source optimal selection for passive location relative navigation under peer-to-peer structure，  the Gauss-Newton method is used to set the initial value of relative navigation Kalman filter to make it converge quickly. With defining time，  position，  geometry and synthetic error factors，  and setting different simulation environments，  the influence of distance，  speed，  time deviation and geometric distribution position on relative navigation accuracy is studied. The simulation results show that the deviation is inversely proportional to the relative navigation accuracy，  and the navigation accuracy is the highest when the connecting angle between the  node to be located and the navigation source is 90°，  the accuracy of the wide baseline scheme is significantly better than that of the narrow baseline scheme when the navigation source  is configured linearly，  and the accuracy of four-source positioning is better than that of two-source or three-source positioning. The algorithm model established in this paper is able to analyze the influence of different factors on positioning errors.

Key words：  peer-to-peer structure; relative navigation; Kalman filter; initial deviation; geometric distribution position; radar signal; target tracking