杨佳明，赵 罡,2，王 伟,3，郭马一，杜孝孝

混合B样条实体模型的等几何拓扑优化

杨佳明1，赵 罡1,2，王 伟1,3，郭马一1，杜孝孝1

(1. 北京航空航天大学机械工程及自动化学院，北京 100191；2. 航空高端装备智能制造技术工业和信息化部重点实验室，北京 100191；3. 北京市高效绿色数控加工工艺及装备工程技术研究中心，北京 100191)

等几何拓扑优化方法将经典拓扑优化理论中的有限元分析过程更改为等几何分析计算，从而提高了拓扑优化的效率与稳定性。针对现有的等几何拓扑优化方法在处理复杂实体结构优化问题时具有一定的局限性，提出一种非结构化样条实体等几何拓扑优化方法。基于混合B样条构造技术，在非结构化六面体网格上构造具有复杂结构的样条实体，并将其作为拓扑优化问题的设计域。用于描述这一样条实体的基函数被直接应用于材料密度分布的表达以及等几何分析计算。在数值算例中，该方法表现出应用于复杂结构时的良好稳定性和鲁棒性。研究成果对等几何拓扑优化方法应用于实际工程问题具有一定的参考意义。

拓扑优化；等几何分析；体参数化；B样条；非结构化样条

拓扑优化是一种重要的工程结构优化方法。目前常见的拓扑优化方法包括：均匀化方法[1]、固体各向同性惩罚微结构模型(solid isotropic microstructures with penalization，SIMP)法[2-3]、渐进结构优化方法[4]、水平集方法[5-7]、移动组件法[8-9]等。由于这些方法可以在设计域中按照给定约束条件高效地搜索最优的设计结构，因此被广泛应用于各类工程问题。其中，AAGE等[10]将千兆体素级的SIMP法应用于全尺寸机翼的结构设计并将该成果发表于《Nature》期刊上，体现了拓扑优化技术的应用潜力。

这些经典的拓扑优化方法一般都会通过有限元方法来实现结构响应的计算。但传统的有限元方法存在以下问题和局限性：①低阶连续性的有限元有可能影响优化计算的准确性并导致数值计算的不稳定 性[11]；②繁琐耗时的有限元前处理过程割裂了几何设计与力学分析过程，从而使拓扑优化难以作为一种设计工具完全融入到现有的计算机辅助设计系统之中。

HUGHES等[12-13]推广的等几何分析方法作为有限元方法，被认为有可能突破上述局限性。其核心思想是直接利用CAD中描述几何模型的样条基函数来表达力学分析中的未知场。由于该方法统一了设计与分析过程中模型的基础表达形式，避免了模型转换引起的误差，因此具有诸多优势。国内外很多学者将其应用于拓扑优化，从而形成了等几何拓扑优化方法。其中，SEO等[14]最先提出在拓扑优化中使用等几何分析方法及裁剪样条曲面；随后，HASSANI等[15]提出了在点密度SIMP法基础上引入NURBS基函数的等几何拓扑优化方法；QIAN[16]将设计域嵌入到一个B样条空间中，证明了基于样条函数的材料密度分布表示方法不仅具有良好的效率和鲁棒性，并且具有固有的过滤性质。国内WANG和BENSON[17]将等几何分析引入到水平集方法中，并针对等几何拓扑优化方法提出了一种高效的计算框架[18]；XIE等[19-20]探索了等几何拓扑优化在移动组件法中的应用；GAO等[21-22]对基于NURBS的等几何拓扑优化方法及相关应用开展了深入的研究。

可以看到，现有的等几何拓扑优化研究大多基于经典的样条构造方法，如B样条、NURBS。而这些张量积样条方法受制于矩形的拓扑结构。尽管可以使用裁剪、拼接等造型方法进行处理，但要保证复杂设计域模型的水密性依旧是一件极具挑战的任务。现有的等几何拓扑优化方法大多只能在简单的矩形设计域上进行验证，制约了在复杂问题上的探索。尤其对于三维实体问题，一些在复杂平面设计域问题中表现良好的方法难以直接推广至实体层面，如ZHAO等[23]提出的基于非结构化T样条曲面的等几何拓扑优化方法。

针对上述问题，本文将一种可以在非结构化体网格上构造样条实体的方法引入等几何拓扑优化。由于允许奇异边(点)的存在，因此可以对高亏格的复杂结构进行表达，突破传统方法的矩形拓扑限制，更符合拓扑优化过程的需求。本文使用WEI等[24]提出的混合B样条构造方法。此方法构造的样条函数不仅具有优良的性质，如非负性、规范性、线性无关性，并且构造过程可靠，具有很好的适应性。本文基于此方法构造非结构化的样条实体模型，并给出了在此类模型上实现等几何拓扑优化的方法，通过算例验证了其可行性，及对复杂实体结构的处理能力。该研究成果有望推动等几何拓扑优化方法在实际工程问题中的应用与推广。

1 混合B样条实体构造方法

本节简要回顾B样条及非结构化六面体网格上的混合B样条构造方法，相关细节可以参考文献[24-25]。

1.1 B样条

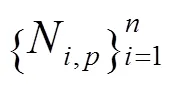
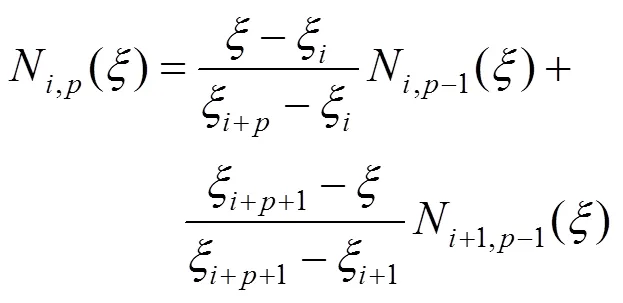
双变量/三变量B样条基函数可以通过单变量B样条基函数的张量积得到。

1.2 混合B样条构造方法

其中，为中的一部分控制顶点。

由节点插入算法[27]可知，，和0之间存在线性变换关系

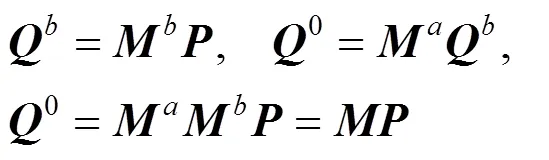
其中，和可以直接通过节点插入算法得到。将其代入式(4)可以得到基函数之间的线性关系

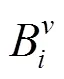
图2 三变量B样条基函数的截断((a)一个C2控制顶点；(b)基函数的等值面；(c) C2控制点周围存在一个激活的C0控制顶点；(d)从中截取后得到的截断基函数的等值面)

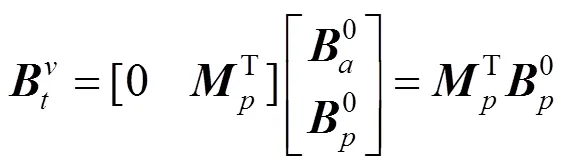
文献[24]将上述情况称为02构造。除此之外，根据激活的0，1控制顶点不同还存在012和02构造形式。相比于012和02，本文采用的02方法尽管在奇异点邻域的连续性上存在不足，但具有构造形式简单以及基函数局部线性无关等优势。

1.3 C02混合B样条实体构造方法

一个非结构化六面体网格中包含了顶点、边、面和体单元4类元素。定义边(顶点)的价为：包含这条边(顶点)的体单元的个数。定义奇异边为：价不为4的内部边以及价不为1或2的边界边。定义奇异点为：奇异边的端点。

如果一个体单元的顶点中包含了奇异点，则称这个体单元为不规则单元。其余的体单元称为规则单元。规则单元又可分为2类：1-邻域内存在不规则单元的规则单元称为规则过渡单元，否则称为规则非过渡单元。图3为一个包含三价奇异边的简单非结构化体网格，并通过颜色区分了不同的单元类型。

图3 非结构化体网格及3种单元类型

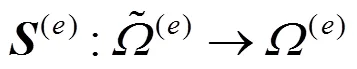
1.3.1 不规则单元

其中，0包含了64个三-三次贝奇尔基函数。

1.3.2 规则非过渡单元

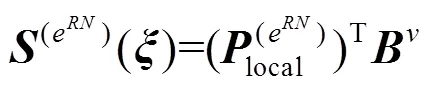
1.3.3 规则过渡单元

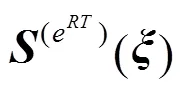
图4 eRT与相邻非规则单元之间不同的相对位置关系

1.3.4 统一构造形式

综上，由式(13)、式(15)和式(17)，可将非结构化六面体网格上的02混合B样条实体构造总结为

可以发现，3类单元均可写为统一的形式，即

1.3.5 连续性

按照式(19)构造的样条实体模型，在规则单元间为2连续，在非规则单元间为0连续，在非规则单元和规则单元间为0连续。02混合B样条实体的连续性分析的简要证明如下：

为了讨论过渡单元与其相邻规则单元间的连续性，引入以下结论：

引理[24]1. 对于任意一个固定的单元，其混合B样条表达形式(式(12))等价于这个单元的B样条表达形式(式(4))。

为了使模型插值于边界，本文将边界单元均按照非规则单元处理。因此，此时边界曲面为0连续曲面。为了提高边界曲面的连续性，可使用非结构化四边形网格的012混合构造方法对其进行处理。当存在原始的B-rep模型时，也可通过调整边界控制顶点使其恢复原始曲面的光顺性。

2 等几何拓扑优化

本节对混合B样条实体的等几何拓扑优化方法进行介绍。为了简化问题的讨论同时又不失一般性，本文着重考虑拓扑优化问题中的最小化柔顺度问题。

2.1 基于混合B样条基函数的材料密度分布

其中，0为材料本身的杨氏模量；min为设定的最小刚度值，用以避免刚度矩阵奇异的情况；为惩罚因子。

2.2 等几何分析

在等几何方法中，可以将静态载荷下线弹性问题的刚度方程表示为

其中，为几何映射(e)的雅可比矩阵。同时，可以通过式(23)对物理域坐标的偏导求得；则通过式(22)表示为

其中，0为杨氏模量等于1时的弹性系数矩阵。

使用高斯积分法来完成式(26)的数值积分运算，则可表示为

2.3 拓扑优化

2.4 灵敏度分析

则目标函数的灵敏度，即式(31)可写为

2.5 优化流程

图5 混合B样条实体等几何拓扑优化流程图

3 数值算例

3.1 算例1

图6(b)为用于构造此设计域样条实体模型的非结构化六面体网格，通过彩色点标出了模型表面的部分奇异点。可以看到本文所使用的构造方法可以支持边界奇异点，以及奇异点相邻的情况。图6(c)和6(d)分别给出了本文构造的02混合B样条实体及其控制顶点分布。此模型的控制顶点数(同时也为设计变量数)为17 745，单元数为540。可以看到模型内部包含了一些奇异边(点)。当直接使用传统张量积样条方法进行构造时，需要考虑多块拼接、裁剪等问题。而本文使用的02混合构造方法在处理时则较为简洁。

图6 算例1的设计域及混合B样条实体模型((a)设计域；(b)用于构造混合B样条实体的非结构化六面体网格；(c)构造的混合B样条实体模型及等几何分析结果(x向位移)；(d)样条实体模型的控制点)

等几何拓扑优化结果如图7(a)所示，最终目标函数值为60.283 8，迭代次数为78。作为对比，图7(b)中展示了SIMP方法的优化结果。该模型的单元数为22 680，最终目标函数值为66.488 1。相比于SIMP方法，本文方法以较少的单元数得到了较好的优化结果(更低的柔顺度)。主要是由于在SIMP方法中，材料密度分布通过离散单元的形式来表达，每一个单元对应一个单一的密度值。而本文方法以连续的样条函数来表达材料密度分布，每个单元都具有内部的密度分布函数，且单元间密度分布连续，因此可以通过较少的单元表达复杂的材料密度分布结构。

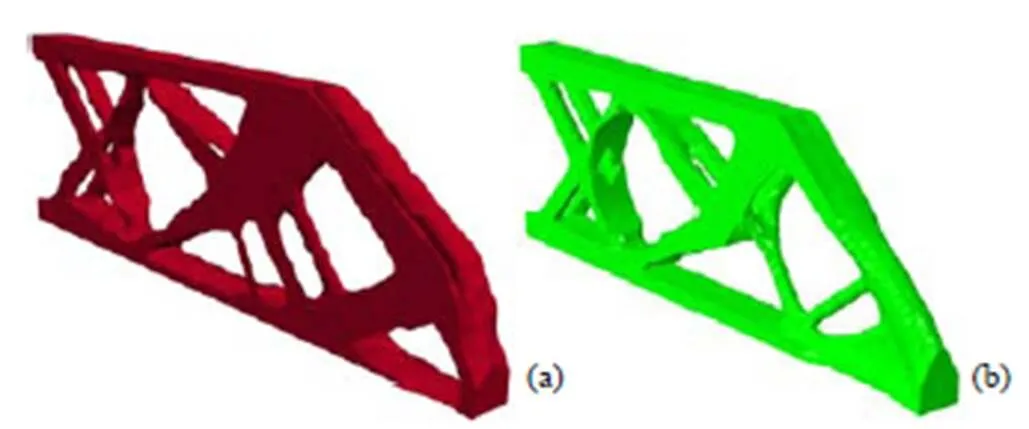
图7 算例1的拓扑优化结果((a)混合B样条实体等几何拓扑优化结果；(b) SIMP法优化结果)

图8为本例中等几何拓扑优化的收敛曲线以及部分中间结果。可以看到整个优化过程的收敛速度较快，且较为光滑，没有出现明显的振荡。说明本文的方法具有较好的收敛性质。

图8 算例1的优化收敛曲线

3.2 算例2

本例为一个复杂实体结构的拓扑优化问题。设计域及边界条件如图9(a)所示，图中红色圆柱面固定，3个角上的蓝色平面施加垂直于平面向外的均布载荷，大小为1。本文将体积分数设为40%，设计变量的初始值为0.4。

图9(b)为用于构造此设计域样条实体模型的非结构化六面体网格。在图9(c)中展示了在样条实体构造过程中识别的不同单元类型。其中，红色为非规则单元，白色为规则单元。规则单元间具有2连续性。图9(d)为最终构造的02混合B样条实体及等几何分析结果。可以看到位移场在模型内部具有较高的连续性。该模型共有162 303个控制顶点，如图10(a)所示。如果完全采用贝奇尔提取方法来处理此样条实体模型，则控制顶点数为197 895，如图10(b)所示。由于02构造方法在模型内部具有更高的连续性，因此使用了更少的控制顶点，其分布更为稀疏，同时减少了设计变量的规模。

图9 算例2的设计域及混合B样条实体模型((a)设计域；(b)用于构造混合B样条实体的非结构化六面体网格；(c)不同的单元类型：红色为非规则单元，白色为规则单元；(d)构造的混合B样条实体模型及等几何分析结果(x向位移))

图11为本例中等几何拓扑优化的结果，最终目标函数值为112.159，迭代次数为100。图12为目标函数收敛曲线、体积分数收敛曲线，以及部分中间结果。可以看到，同算例1，在本例中优化收敛速度较快，无明显振荡，说明本文方法在处理复杂结构时也具有较好的稳定性和鲁棒性。

图10 混合B样条实体与完全采用贝奇尔提取方法时的控制顶点分布对比，图中每一个红色点表示一个控制顶点，红色点越密集的区域控制顶点数目越多((a)混合B样条实体的控制顶点分布；(b)完全采用贝奇尔提取方法时的控制顶点分布)

图11 算例2的等几何拓扑优化结果

图12 算例2的优化收敛曲线

3.3 算例3

本例为一个多工况复杂实体结构的拓扑优化问题。设计域及2个工况状态如图13(a)和图13(b)所示。图中4个红色圆柱面固定。在工况1时两侧悬臂的蓝色圆柱面区域分别受到轴正向和负向的载荷，大小为1。在工况2时两侧悬臂的蓝色圆柱面区域分别受到轴正向和负向的载荷，大小为1。取体积分数约束为30%。

按照本文方法所构造的样条实体如图13(c)所示，图中同时显示了工况1下的等几何分析结果。此模型的控制顶点分布如图13(d)所示，总个数为110 283。可以看到由于此模型包含了多个孔洞结构，因此如果直接使用张量积NUBRS实体进行构造将会遇到很大困难。

图13 算例3的设计域及混合B样条实体模型((a)设计域及工况1；(b)设计域及工况2；(c)构造的混合B样条实体模型及等几何分析结果(z向位移)；(d)样条实体模型的控制点)

在优化过程中本文设定目标函数为2种工况下柔顺度的平均值。等几何拓扑优化结果如图14所示，最终目标函数值为141.173，其中工况1的柔顺度为267.901，工况2为14.445，迭代次数为100次。此算例进一步证明了该方法在复杂实体结构拓扑优化问题中具有良好的适应性。

图14 算例3的等几何拓扑优化结果

4 结束语

本文针对现有等几何拓扑优化方法难以处理复杂实体结构设计域这一问题，提出了一种基于混合B样条构造的非结构化样条实体等几何拓扑优化方法。此方法可在非结构化六面体网格上构造具有一定内部连续性的样条实体。本文将构造得到的样条基函数直接用于描述拓扑优化问题中的材料密度分布，以及结构响应计算中的未知场。给出了等几何拓扑优化表达式以及相应的灵敏度计算公式。最后，通过3个算例验证了本文方法在处理复杂结构优化问题时的有效性和稳定性。在这一研究成果基础之上，有望形成面向实际工程中复杂模型的等几何拓扑优化设计工具。在后续研究中，如何提高奇异点邻域的连续性将会是一个关键的研究方向。

[1] BENDSØE M P, Kikuchi N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[2] Zhou M, Rozvany G I N. The COC algorithm, part II: topological, geometry and generalized shape optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 89(1-3): 309-336.

[3] BendsØe M P, Sigmund O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9-10): 635-654.

[4] Xie Y M, Steven G P. A simple evolutionary procedure for structural optimization[J]. Computers & Structures, 1993, 49(5): 885-896.

[5] Sethian J A, Wiegmann A. Structural boundary design via level set and immersed interface methods[J]. Journal of Computational Physics, 2000, 163(2): 489-528.

[6] Wang M Y, Wang X, Guo D. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(1-2): 227-246.

[7] Allaire G, Jouve F, Toader A M. Structural optimization using sensitivity analysis and a level-set method[J]. Journal of Computational Physics, 2004, 194(1): 363-393.

[8] Guo X, Zhang W S, Zhong W L. Doing topology optimization explicitly and geometrically - a new moving morphable components based framework[J]. Journal of Applied Mechanics, 2014, 81(8): 081009.

[9] Zhang W S, Song J F, Zhou J H, et al. Topology optimization with multiple materials via Moving Morphable Component (MMC) method[J]. International Journal for Numerical Methods in Engineering, 2017, 113(11): 1653-1675.

[10] Aage N, Andreassen E, Lazarov B S, et al. Giga-voxel computational morphogenesis for structural design[J]. Nature, 2017, 550: 84-86.

[11] Sigmund O, Petersson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural and Multidisciplinary Optimization, 1998, 16(1): 68-75.

[12] Hughes T J R, Cottrell J A, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39-41): 4135-4195.

[13] Cottrell J A, Hughes T J R, Bazilevs Y. Isogeometric analysis: toward Integration of CAD and FEA[M]. Chichester: John Wiley & Sons, 2009: 1-18.

[14] Seo Y D, Kim H J, Youn S K. Isogeometric topology optimization using trimmed spline surfaces[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(49-52): 3270-3296.

[15] Hassani B, Khanzadi M, Tavakkoli S M. An isogeometrical approach to structural topology optimization by optimality criteria[J]. Structural and Multidisciplinary Optimization, 2012, 45(2): 223-233.

[16] Qian X P. Topology optimization in B-spline space[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 265(1): 15-35.

[17] Wang Y J, Benson D J. Isogeometric analysis for parameterized LSM-based structural topology optimization[J]. Computational Mechanics, 2016, 57(1): 19-35.

[18] Wang Y, Liao Z Y, Ye M, et al. An efficient isogeometric topology optimization using multilevel mesh, MGCG and local-update strategy[J]. Advances in Engineering Software, 2020, 139: 102733.

[19] Xie X D, WANG S T, Xu M M, et al. A new isogeometric topology optimization using moving morphable components based on R-functions and collocation schemes[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 339(1): 61-90.

[20] Gai Y D, Zhu X F, Zhang Y J, et al. Explicit isogeometric topology optimization based on moving morphable voids with closed B-spline boundary curves[J]. Structural and Multidisciplinary Optimization, 2019, 61: 963-982.

[21] Gao J, Luo Z, Xiao M, et al. A NURBS-based Multi-Material Interpolation (N-MMI) for isogeometric topology optimization of structures[J]. Applied Mathematical Modelling, 2020, 81: 818-843.

[22] Gao J, Xue H P, Gao L, et al. Topology optimization for auxetic metamaterials based on isogeometric analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 352(1): 211-236.

[23] Zhao G, Yang J M, Wang W, et al. T-splines based isogeometric topology optimization with arbitrarily shaped design domains[J]. Computer Modeling in Engineering and Sciences, 2020, 123(3): 1033-1059.

[24] Wei X D, Zhang Y J, Toshniwal D, et al. Blended B-spline construction on unstructured quadrilateral and hexahedral meshes with optimal convergence rates in isogeometric analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 341(1): 609-639.

[25] Wei X D, Zhang Y J, Hughes T J R. Truncated hierarchical tricubic C0 spline construction on unstructured hexahedral meshes for isogeometric analysis applications[J]. Computers & Mathematics with Applications, 2017, 74(9): 2203-2220.

[26] Giannelli C, Jüttler B, Speleers H. THB-splines: the truncated basis for hierarchical splines[J]. Computer Aided Geometric Design, 2012, 29(7): 485-498.

[27] Boehm W. Inserting new knots into B-spline curves[J]. Computer Aided Design, 1980, 12(4): 199-201.

[28] Scott M A, Simpson R N, Evans J A, et al. Isogeometric boundary element analysis using unstructured T-splines[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 254: 197-221.

[29] Bendsøe M P, Sigmund O. Topology optimization: theory, methods, and applications[M]. Heidelberg: Springer, 2004: 9-28.

[30] Svanberg K. The method of moving asymptotes - a new method for structural optimization[J]. International Journal for Numerical Methods in Engineering, 1987, 24(2): 359-373.

Isogeometric topology optimization of blended B-spline solid model

YANG Jia-ming1, ZHAO Gang1,2, WANG Wei1,3, GUO Ma-yi1, DU Xiao-xiao1

(1. School of Mechanical Engineering & Automation, Beihang University, Beijing 100191, China;2. Key Laboratory of Aeronautics Smart Manufacturing, Ministry of Industry and Information Technology, Beijing 100191, China;3. Beijing Engineering Technological Research Center of High-Efficient & Green CNC Machining Process and Equipment, Beijing 100191, China)

For isogeometric topology optimization (ITO) methods, isogeometric analysis (IGA) is adopted for topology optimization to address the limitation of the finite element method, which can improve the efficiency and stability of the optimization. However, it is of great challenge for existing ITO methods to manage arbitrarily shaped design domains, especially in three-dimensional solid problems. Therefore, a new ITO method was proposed to handle unstructured solid models. A spline solid with complex structures was obtained from an unstructured hexahedral mesh based on the blended B-spline construction. The basis functions describing the unstructured spline solid were applied to the representation of density distribution and the calculation of IGA. Several examples proved the flexibility and robustness of the proposed method in dealing with complex structures. These results may shed light on the application of ITO in practical engineering problems.

topology optimization; isogeometric analysis; volume parameterization; B-spline; unstructured splines

TP 391

10.11996/JG.j.2095-302X.2021030501

A

2095-302X(2021)03-0501-10

2020-09-17；

2020-10-15

17 September，2020；

15 October，2020

国家自然科学基金项目(61972011，61572056)

National Natural Science Foundation of China (61972011, 61572056)

杨佳明(1995-)，男，北京人，博士研究生。主要研究方向为等几何拓扑优化、T样条。E-mail：yangjiaming@buaa.edu.cn

YANG Jia-ming (1995-), male, PhD candidate. His main research interests cover isogeometric topology optimization and T-splines. E-mail: yangjiaming@buaa.edu.cn

王 伟(1978-)，男，河北衡水人，副教授，博士。主要研究方向为CAD/CAE、智能计算等。E-mail：jrrt@buaa.edu.cn

WANG Wei (1978-), male, associate professor, Ph.D. His main research interests cover CAD/CAE, intelligence computation, etc. E-mail：jrrt@buaa.edu.cn