广东省惠州市惠阳区崇雅实验学校(516211) 王瑞生

教学活动中,应结合教学任务及其蕴合的数学学科核心素养设计合适的情境和问题, 引导学生用数学的眼光观察现象、发现问题,使用恰当的数学语言描述问题,用数学的思想、方法解决问题.在问题解决的过程中,理解数学内容的本质,促进学生数学学科核心素养的形成和发展[1].

特殊与一般思想是数学的重要思想之一,数学公式、定理、法则的学习通常就是先从特殊开始,再总结归纳,后经过证明得到一般性结论,又使用一般性结论来解决相关的数学问题.这种由特殊到一般再由一般到特殊反复认识的过程,正是这一数学思想的具体体现.

数学高考中, 特殊与一般思想的考查方式通常表现为:字母表示数、归纳猜想、构造函数、应用特殊图形、探求特殊点等等.高考试题常通过选择题、填空题考查由特殊到一般,借助解答题的严谨性综合考查特殊与一般的数学思想.

下面以2020年高考数学全国I 卷理科几例典型试题在教学中的情境创设及“问题串”的引导,感悟特殊与一般数学思想的应用.

1 创设数学文化情境,用字母表示数的一般性

例1(2020年高考数学全国新课标I 卷理科第3 题)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )

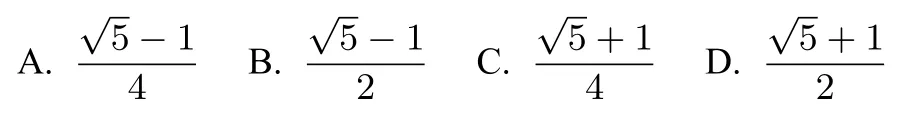
情境设计:《九章算术·商功》:“阳马居二,鳖臑居一,不易之率也.”今称为刘徽原理.刘徽注《九章算术》关于体积问题的论述已接触到现代体积理论的核心问题.

阳马: 中国古代算数中的一种几何形体,是底面为长方形,两个三角面与底面垂直的四棱锥体.

投影胡夫金字塔图片.

图1

图2

问题1: (1)金字塔的形状可以联想到哪一类空间几何体?

(2)能描述该类几何体的结构特征吗?

投影2020年高考数学全国新课标I 卷理科第3 题.

问题2: (1)四棱锥的高、侧面三角形底边长如何表示?

(2)探究正四棱锥的基本量的关系?

设计意图由《九章算术》中的阳马引入四棱锥,展示中华悠久的数学文化成就,落实立德树人的教育目标,同时为引导同学们将胡夫金字塔直观联想为正四棱锥做铺垫.

将数学文化渗透在日常教学中,引导学生了解数学的发展历程,认识数学在科学技术、社会发展中的作用,感悟数学的价值,提升学生的科学精神、应用意识和人文素养,将数学文化融入教学,还有利于激发学生的数学学习兴趣,有利于学生进一步理解数学,有利于开拓学生视野、提升数学学科核心素养[1].

通过问题1 将胡夫金字塔抽象为正四棱锥,让学生感受现实生活问题抽象为数学模型,体现数学源于对现实世界的抽象,又服务于生活的基本理念,培养学生的直观想象、数学建模等数学核心素养.正四棱锥是特殊的多面体,追问“能说出该几何体的结构特征吗? ”目的是启发学生独立思考,引导学生把握数学内容的本质.运用直观感知、推理论证、度量计算等认识和探索几何体的结构特征,探究空间几何图形的性质,方可建立空间概念.

该题目条件中没有给出四棱锥的高、侧面三角形底边长的相关数据,怎么计算? 问题2 意在引导学生用字母表示高、边长等数学量,可设正四棱锥的高为h、底面边长为a,用字母表示数是一般性的应用.追问(2)引导学生将空间问题平面化,把线段、角看作三角形的边、内角,通过构造直角三角形探求基本量的关系.

问题2 重在培养学生数据处理、数学运算等数学核心素养.

立体几何初步的教学重点是帮助学生逐步形成空间观念,应遵循从整体到局部、从具体到抽象的原则,提供丰富的实物模型呈现空间几何体,帮助学生认识空间几何体的结构特征,进一步掌握在平面上表示空间图形的方法和技能[1].

2 创设现实情境,构造特殊函数

例2(2020年高考数学全国新课标I 卷理科第12 题)若2a+log2a=4b+2log4b,则( )

A.a ＞2bB.a ＜2bC.a ＞b2D.a ＜b2

情境设计: 播放视频: 2019年4月12日,天津杨村,飞机的轰鸣声响彻云霄,单机大仰角上升、四机向上开花……被誉为“蓝天仪仗队”的空军八一飞行表演队驾驶歼-10 表演机,为观众献上了一场精彩的视觉盛宴.“场面太震撼了,我为祖国有这样棒的飞机骄傲.”一位专程从山东赶来观看表演的王先生激动地对记者说.

问题1: (1)歼-10 特技动作是集飞行员素质、数学与科技的融合,歼-10 单机大仰角上升在空中划出一道优美的曲线,同学们会联想到哪一类基本初等函数?

(2)了解互为反函数吗?

问题2: 观察等式两边的结构特征,应如何变形?

问题3: (1)观察选项,对变形后的等式有何想法?

(2)观察化归后的不等式,发现什么?

(3)相同的作为常量,不同的a与2b作为变量,可构造函数____.

设计意图在“我为祖国有这样棒的飞机骄傲”的激动声音中感受祖国的强大,培养同学们的民族自信心和自豪感,增强社会责任感;让数学为学生形成正确人生观、价值观、世界观等方面发挥独特作用.特技“大仰角上升”形象的描绘出单调递增的指数函数图像,顺势引入指数函数y=ax(a ＞0且a/=1),通过追问(2),由数学概念“互为反函数”把对数函数y= logax(a ＞0 且a /= 1)和指数函数有机的结合在一起,起到承上启下的作用.而“优美”一词旨在让同学们体会曲线之美到数学之美的同时,借图象揭示函数性质,并在现实问题中利用函数构建模型,解决问题.培养学生直观想象、数学建模等核心素养.

问题2 观察等式的结构特征,就是有意识的让同学们感知数与形的特点,对字母、数字、符号或文字所表达的数学关系式的结构进行观察,培养数学观察力是实现教学目标和提高学生数学素养的需要.同学们可以发现“等式两边的代数式底数虽不同,但可化为同底”,即2a+log2a=22b+log2b.

问题3 递进式引入,引导同学们分析题干和选择支的信息,将问题适当加工处理,构造与问题相关的数学模型,揭示其本质.

由对数函数单调性可得2a+ log2a= 22b+ log2b ＜22b+log22b,构造分别以a,2b为变化量的不等关系式,将问题引向函数性质的应用.

在此,问题(1)是方向,问题(2)就是该题的灵魂——构造特殊函数.

再次引导学生观察: 发现两个式子为a,2b的同构式(数学中把除了变量不同,而结构相同的两个表达式称为同构式.如果不等式两侧呈现同构特征,可将相同的结构构造为一个函数,进一步与函数的单调性取得联系),进而将同构式视为函数f(x)=2x+log2x,而a,2b为该函数的两个自变量,构造函数,通过研究其单调性比较自变量a与2b的大小.

数学同构式彰显了数学的对称和谐美,构造同构式的解题策略,培养了学生的抽象、转化化归等数学思维能力.

帮助学生学会用函数图象和代数运算的方法研究这些函数的性质;理解这些函数中所蕴含的运算规律;运用这些函数建立模型,解决简单的实际问题,体会这些函数在解决实际问题中的作用[1].

可以看出,只有将条件等式化归为含有a与2b或a与b2的关系式,才能比较其大小关系.

3 创设科学情境,探求特殊点

例3(2020年高考数学全国新课标I 卷理科第20 题)已知A、B分别为椭圆E:+y2= 1(a ＞1)的左、右顶点,G为E的上顶点,= 8,P为直线x= 6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求E的方程;

(2)证明: 直线CD过定点.

情境设计: 几何画板演示: 椭圆E:+y2=1(a ＞1)的左右顶点分别为A、B,P为直线l:x=t(t ＞a)上的动点,PA与E的另一交点为C,PB与E的另一交点为D,得直线CD.拖动点P沿直线l上下运动,让同学们观察动直线CD的运动特征.

问题1: (1)取a= 2,t= 4 时,请同学们观察直线CD运动过程中有何发现?

(2)取a=3,t=3 时,请同学们观察直线CD运动过程中有何发现?

(3)大家发现直线CD运动变化过程中的规律吗?

投影例3(2020年高考数学全国新课标I 卷理科第20 题)

问题2: (1)能说出直线CD所经过定点的坐标吗?

(2)你能先求出该定点的坐标吗?

(3)已经知道直线CD所经过定点的坐标,要想证明直线CD过该定点,需要证明什么?

问题3: 同学们能归纳出一般性结论吗? 试着证明一下.

设计意图几何画板形象、动态、科学的演示试验,让同学们直观观察在椭圆变化、直线l左右运动、动点P上下运动的情况下,直线CD的“动中有定”的运动变化规律.

问题1 先观察特殊再归纳一般, 借助几何画板中的椭圆、直线、点的可运动变化特性观察特殊状态和一般状态: 当a= 2,t= 4 或a= 3,t= 3 时,拖动点P沿直线l上下运动,同学们可以直观观察出直线CD分别围绕定点(1,0)或(3,0)旋转运动.变换a、t的取值,通过(3)让学生发现一般性规律: 动直线CD恒过定点应用几何画板不仅建立了形与数的联系,同时体现由特殊到一般数学思想.

问题2(1)“说”出定点坐标,是将一般结论特殊化.既是问题1 的延伸,又是提醒“证明直线过定点”问题中的定点是可以预知的,为(2)作铺垫.

求动直线经过的定点坐标方法有: 点斜式方程法、比较系数法、直线系法、特例验证法等.(2)中的“先”意在引导同学们考虑特例验证法,即在直线x=6 上取点P的两个特殊位置,得到两条直线,求其交点Q即可.多数同学可以联想到利用特殊化思想,迅速求出定点坐标.

问题(3)综合考查三点共线的证明方法: 定点Q坐标满足直线CD的方程;直线CQ与直线DQ的斜率相等;直线CQ与直线DQ的方向向量共线.同学们可根据自己掌握知识情况进行选择相应的方法,培养逻辑推理、数据处理、数学运算等数学核心素养.

问题2 呈现证明直线过定点时: 先特殊,后验证一般的特殊与一般数学思想的应用.

问题3 以归纳法呈现特殊与一般数学思想的同时,重在引导学生对问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的数学建模素养.

随着《普通高中数学课程标准(2017 版)》的实施,基于数学学科核心素养的教学活动应该把握数学的本质,创设合适的教学情境、提出合适的数学问题,引发学生思考与交流,形成和发展数学学科核心素养.以上典例分别采用创设数学情境、现实情境、科学情境,并以“问题串”逐步引导学生分析问题、解决问题,建构特殊与一般数学思想,让学生在熟悉、关联、综合的课堂情境中化一般为特殊、由特殊到一般,使问题化难为易、化繁为简,收到良好的教学效果.

4 教学反思

题海战术学习数学难以取得理想效果,学生提高数学解题能力和意识就要注重数学思想的领会和运用.如遇到一些较难问题,若从特殊情况进行分析,会使问题迎刃而解,特殊化思想往往孕育着一般问题的解决方法,因此,教师应将数学思想渗透贯穿于教学全过程,注重凝炼典型问题中的数学思想,强化应用意识,抓本质促能力.

用字母表示数、构造特殊函数等数学方法都是一般与特殊数学思想的产物,正确的数学思想指导有效的数学解题方法.

同时,《普通高中数学课程标准(2017 版) 》明确指出:“设计合适的教学情境,提出合适的数学问题是有挑战性的,也为教师的实践创新提供了平台.教师应不断学习、探索、研究、实践,提升自身的数学素养,了解数学知识之间、数学与生活、数学与其他学科的联系,开发出符合学生认知规律、有助于提升学生数学学科核心素养的优秀案例.”