杜 鑫, 胡 正, 王建英

(1.上海大学机电工程与自动化学院, 上海 200444; 2.上海大学计算中心, 上海 200444)

许多工程实际中的系统通过机理建模通常会导致复杂的高阶数学模型, 而直接使用这些高阶模型通常会给后续系统仿真、分析、综合带来数值计算及物理实现上的困难, 因此需要通过模型降阶方法来生成一个与原始系统具有相似响应特性的低复杂度的降阶模型[1-3].在控制理论、计算数学等领域中被广泛接受的模型降阶方法包括平衡截断法[4]、矩匹配法(Krylov 子空间法)[5]、本征正交分解[6].起源于控制系统主元分析的平衡截断法由于其算法简洁, 同时可以给出合理的先验误差上界, 被视为解决线性时不变系统以及诸多含有复杂动态特性的类线性系统模型降阶问题的一个较好的理论框架.

切换系统是指由一组连续或离散动态子系统组成, 并按某种切换律在各子系统间切换的动力系统, 许多工程系统如电力电子系统、输电系统、飞行器控制系统、机器人控制系统等,都需要采用切换系统模型来描述其固有的动态特性.切换系统在过去30 多年间一直是控制与系统领域的研究热点之一[7-10].近年来切换系统的模型降阶问题得到了许多学者的关注, 并涌现出了一系列相关成果[11-28], 其中绝大多数工作都与平衡截断法直接或间接相关.Petreczky等[14-15]借助线性矩阵不等式定义并求解共同可控/可观格拉姆矩阵, 进而给出可生成与线性时不变系统情形下相同形式误差界的平衡截断算法; Shaker 等[16-17]在此基础上考虑了频率受限情形下的切换系统模型降阶.针对离散时间切换系统, Birouche[18]提出了通过求解各子系统相关的可控/可观格拉姆矩阵来实现平衡截断模型降阶.通过矩阵不等式求解切换系统格拉姆矩阵的思想在马尔可夫切换系统的模型降阶问题中也得到了相应的推广[19-22], 但这类方法需要通过线性矩阵不等式计算来求解所需格拉姆矩阵, 计算复杂度较高, 仅适用于求解小规模切换系统的模型降阶问题.Monshizadeh 等[23]针对状态矩阵可交换的任意切换线性系统, 将共同可控/可观格拉姆矩阵定义为一组特殊矩阵方程的解, 进一步给出了保持状态矩阵可交换性的平衡截断算法.注意到切换系统与双线性系统结构上的相似之处, Duff等[24]提出了基于双线性结构描述下系统可控/可观格拉姆矩阵的平衡截断算法; Strom 等[25]通过对切换系统无限能量格拉姆矩阵的深入研究, 给出了可提供L2 诱导范数意义下误差界的平衡截断算法.

周期切换系统是一类在航空系统、开关电源、多速率采样系统等领域具有重要现实意义的切换系统[26-29].对离散时间周期切换系统的模型降阶的研究开展较早.如通过采用系统提升(lifting)技术将周期切换系统转换为一个高维的线性时不变系统, Varga[30]给出了相应的平衡截断模型降阶算法; Farhood 等[31]进一步完善了该方法; Hossain 等[32]和Benner 等[33]针对广义周期切换系统进一步给出了该方法的推广形式, 并给出了适用于大规模周期切换系统的Lyapunov 方程低秩快速求解数值算法; 通过引入“快照”法求解近似格拉姆矩阵的思想,Ma等[34]给出了一类可实现快速求解的离散时间周期切换系统模型降阶方法.但是, 针对连续时间周期切换系统, 目前还未见较好的模型降阶方法报道.

在电力电子系统如Buck/Boost 变换器中, 子系统间的切换速率很快, 切换信号通常为高频的周期性信号, 本工作针对这类快速周期切换系统的模型降阶问题展开研究.一方面, 通过引入状态平均法, 即首先求取给定周期切换系统的直流平均模型以及交流小信号平均模型来描述其在直流输入和交直流输入情形下的“平均”动态特性[35-36]; 另一方面, 结合两类平均模型中参数矩阵的结构特性, 应用奇异摄动平衡截断理论分别给出了相应的降阶周期切换各子系统模型参数的两类求解算法.两类算法均保持了快切换条件下的系统稳定性, 同时在“平均”动态特性意义下给出了相应的模型逼近误差性能先验分析.最后, 应用仿真算例说明了所提算法的有效性和优越性.

1 问题描述

考虑连续时间周期切换线性系统

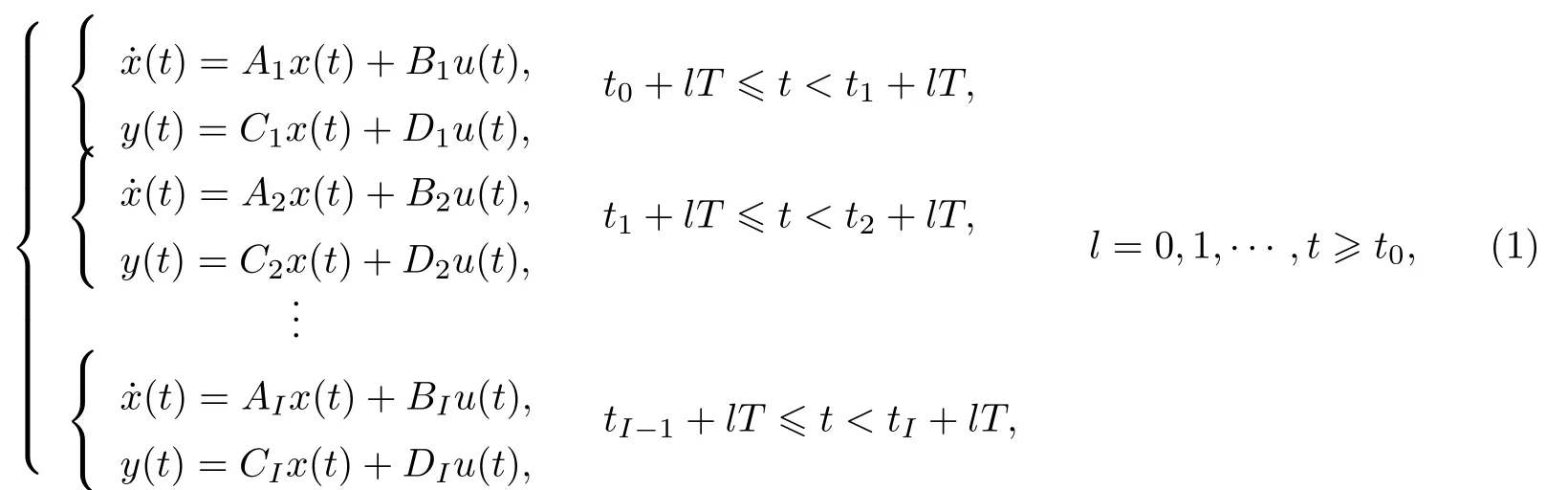
式中:x(t)∈Rn是状态向量;y(t)∈Cp是输出信号;u(t)∈Rm是输入信号; 切换周期为T,在每个周期中第i个子系统(Ai,Bi,Ci,Di)的激活时长为∆tk=ti −ti−1.定义一组周期切换信号pi(t),

则周期切换系统(1)可以表示为

式中:

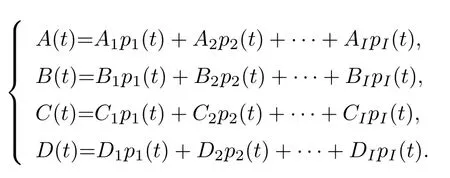
本工作主要考虑快周期切换系统(即切换周期T较小)的模型降阶问题, 即通过数学方法在已知给定切换系统模型的基础上求取一个低阶的快周期切换系统模型

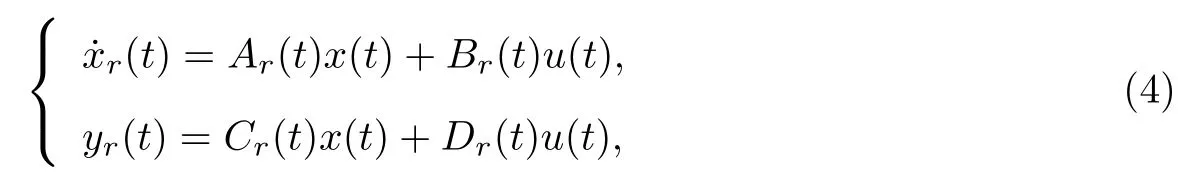
近似地描述给定周期切换系统(1)的输入输出动态特性, 同时保持原系统的稳定性等基本性质.(Ar(t),Br(t),Cr(t),Dr(t))由待求的低阶子系统模型参数(Ari,Bri,Cri,Dri,i= 1,2,··· ,I)和与原系统相同的周期切换信号pi(t)组成, 即

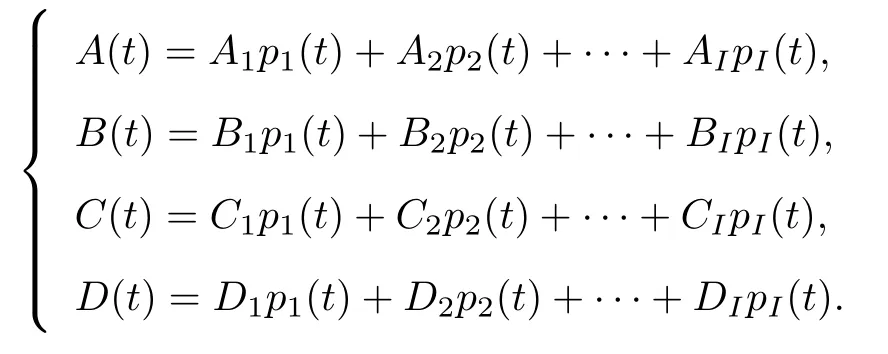
2 周期快切换系统平衡截断模型的降阶

2.1 基于稳态线性平均模型

状态空间平均法是平均法的一阶近似, 是电力电子系统(如各种类型的DC-DC 转换器)进行瞬态建模分析的常用方法.定义第i个子系统的占空比为

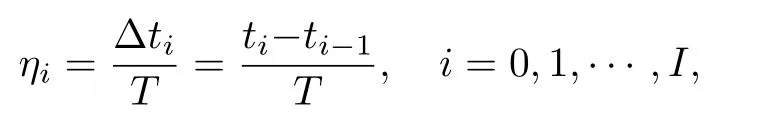
系统的平均状态为

式中:x(t)为周期切换系统的真实状态.通过一阶近似法, 容易得到周期切换系统的直流平均模型

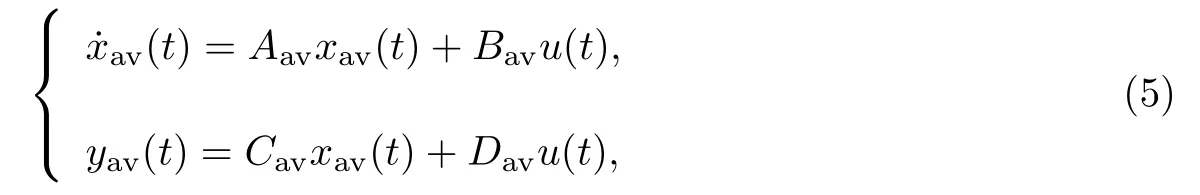
式中:

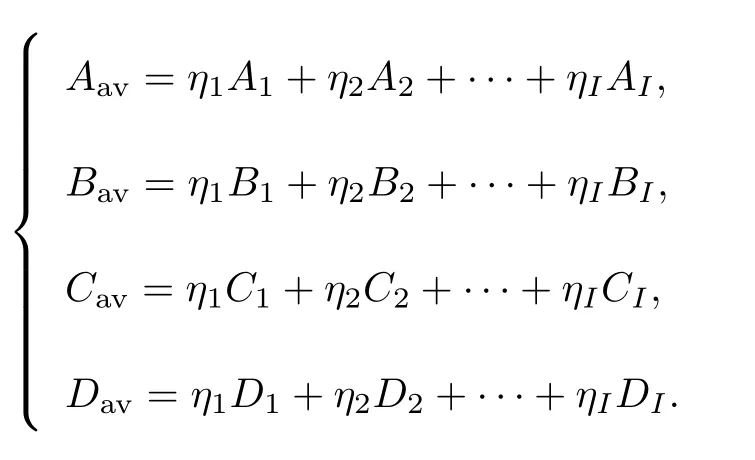
借助状态空间平均模型(5), 可以采用线性时不变系统的方法和工具分析周期切换系统的稳态特性, 同时还可以得到周期切换系统的一个弱稳定性分析条件.

引理1[26-27]考虑周期切换系统(1), 如果其状态空间平均模型稳定, 即Aav为Hurwitz 矩阵, 则一定存在足够快的切换频率f=1/T使得周期切换系统(1)稳定.

基于线性时不变的状态空间平均模型(5), 给出借助奇异摄动型平衡截断的算法来求解降级的各周期切换子系统模型参数矩阵.

算法1基于直流平均模型的切换系统平衡截断模型降阶.

输入: 给定线性切换系统模型(Ai,Bi,Ci,Di)以及降阶模型数r.

(1) 求解关于平均状态空间模型的可控/可观Lyapunov 方程:

(2) 对矩阵进行Cholesky 分解:=Uav.

(3) 对矩阵av进行特征值分解:=Vav, 其中Σav= diag{σav1,σav2,··· ,σavn}.

(4) 计算相应的坐标变换矩阵:Tav=.

(5) 通过坐标变换计算给定稳态平均模型的平衡实现以及各切换子系统模型的平衡实现:

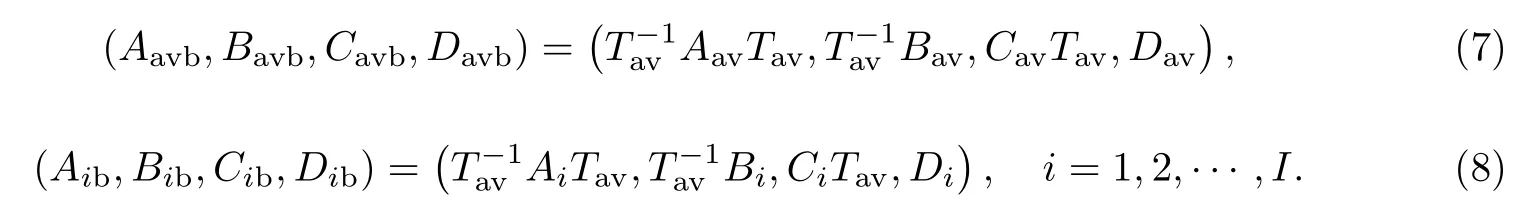
(6) 根据待求解降阶模型阶数r对各平衡实现下的状态空间参数矩阵进行分块, 可得

式中:Aavb11,Aib11∈Rr×r;Bavb1,Cib1∈Rr×p;Cavb1,Cib1∈Rm×r.进而, 根据

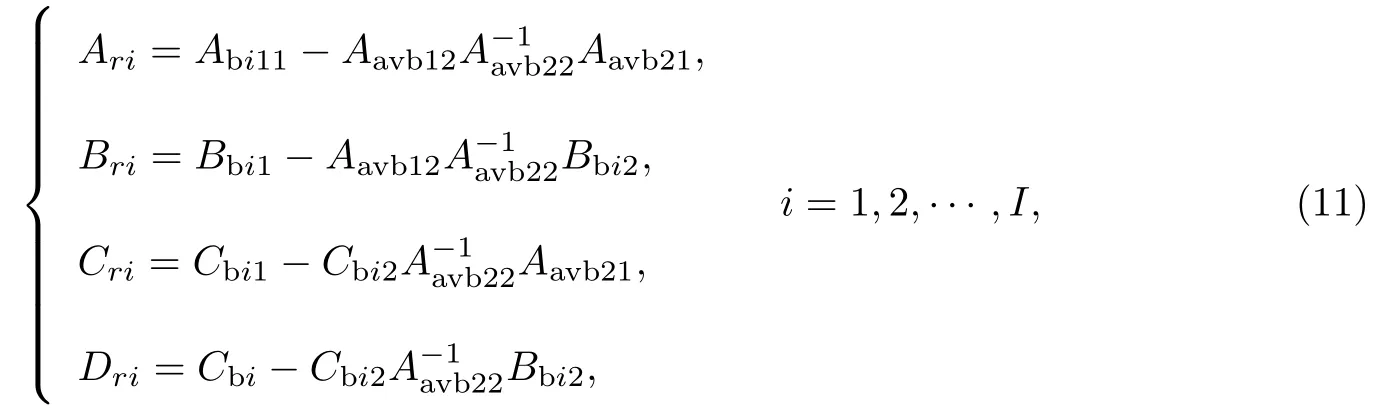
生成待求的降阶快周期切换系统各子系统模型参数矩阵.

输出: 低阶线性切换系统模型(Ari,Bri,Cri,Dri).

定理1算法1 生成的降阶周期切换系统同样满足弱稳定性(即存在足够高的切换频率使得其稳定), 降阶周期切换系统的直流平均模型与原周期切换系统的直流平均模型(5)在直流输入下的误差为0, 即

同时, 在全频域上的逼近性能存在H∞范数意义下的误差界:

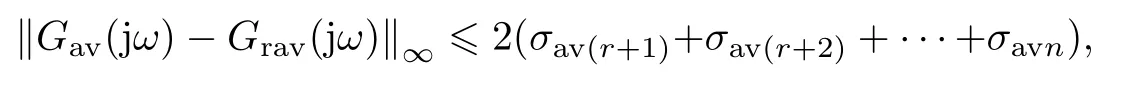
其 中Grav(jω) =Crav(jωI −Arav)−1Brav+Drav为 降 阶 周 期 切 换 系 统 直 流 平 均 模 型(Arav,Brav,Crav,Drav)的传递函数.

证明 设()为直流平均模型(5)采用奇异摄动平衡截断所生成的降阶模型.结合式(5)中关于周期切换系统直流平均模型的定义以及算法1 中降阶周期切换系统各子系统模型参数的计算公式, 可推得

不难看出, 降阶周期切换系统的直流平均模型Grav(jω)(Arav,Brav,Crav,Drav)与直接对原系统直流平均模型进行奇异摄动平衡截断模型降阶所得线性时不变模型(jω)()完全一致, 根据奇异摄动平衡截断理论[1-3]可知,为Hurwitz 矩阵且满足

其中(jω) =(j)−1+为相应线性时不变降阶系统的传递函数.进一步根据引理1 可知, 降阶周期切换系统具有快切换条件下的弱稳定性, 同时定理1 中描述的频域逼近性能成立, 即有

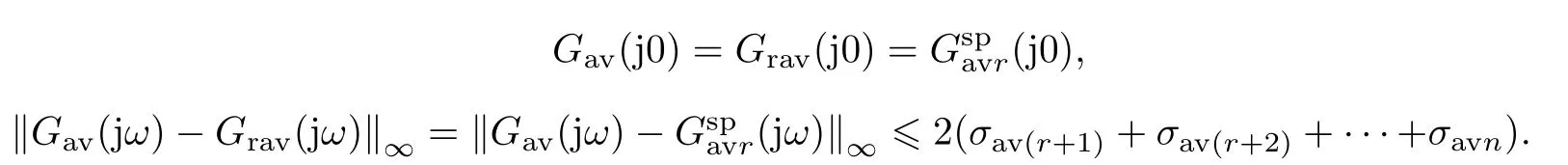
注1针对线性时不变系统的模型降阶问题, 平衡截断法有标准型和奇异摄动型2 种生成相同全频域误差上界的降阶系统参数矩阵求解形式, 采用标准型平衡截断法可得到较好的高频段模型逼近性能(其中降阶模型与原模型在ω=∞处完全匹配), 而采用奇异摄动型平衡截断法则可得到较好的低频段模型性能(其中降阶模型与原模型在ω=0 处完全匹配), 关于这2种类型的平衡截断详细介绍见文献[1,3].当系统输入为直流信号即零频信号时, 在算法1 中对直流平均模型采用奇异摄动型平衡截断显然更为合理.

2.2 基于交流小信号平均模型

对于许多实际周期切换系统, 其输入往往存在直流信号之外的交流摄动信号, 且交流摄动信号的幅度远小于直流信号.此外, 系统的切换时间也有可能存在摄动.在这种情况下通常采用小信号方法来建立周期切换系统的交流小信号平均模型, 进行系统动态分析[35].如果系统的切换频率远大于系统的自然频率以及交流摄动信号的频率, 则交流小信号平均模型可以很好地描述系统在交流摄动情形下的动态响应特性[36].

首先, 假设周期切换系统在直流输入u(t) =U会达到一个平衡态X, 该平衡态由下列方程建立:

当输入信号中叠加有小的交流摄动摄动信号时(即u(t) =U+uac(t), 其中uac(t)表示小的交流摄动信号), 令ηi(t)=ηi+ηpi(t)表示第i个子系统在一个周期内的激活时间函数, 其中ηpi(t)上的摄动相应的系统的状态x(t)、输出y(t)以及占空比均可表示为下列稳态加摄动的形式:

将式(13)带入系统的动态方程(1), 可得

进一步整理式(14), 可得

根据式(12), 可以消掉式(15)中的直流项.此外, 基于交流摄动为小信号的假设, 忽略式(15)中微小的二次非线性项不会带来严重的系统分析误差, 因此可得到如下线性的交流小信号平均模型:

式(16)可进一步整理为

式中: 系统矩阵(Aav,Bav,Cav,Dav)及输入信号¯up(t)分别为

其中

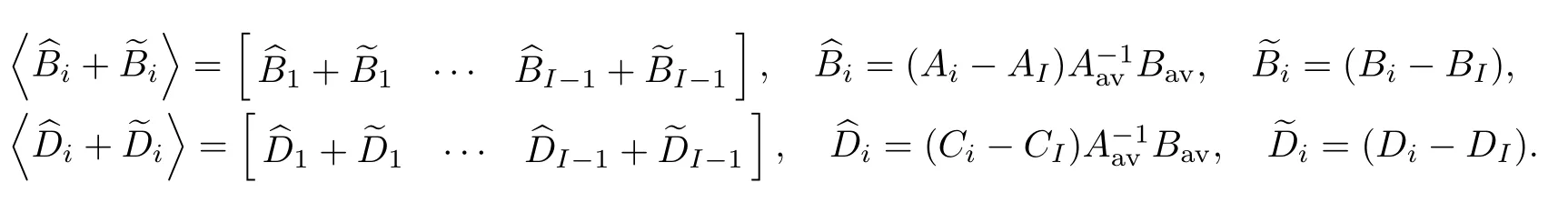
基于上述周期切换系统的交流小信号平均模型, 下面给出结合标准平衡截断法的周期切换系统模型降阶算法

算法2基于小信号交流平均模型的切换系统平衡截断模型降阶算法.

输入: 给定线性切换系统模型(Ai,Bi,Ci,Di)以及降阶模型数r.

(1) 求解关于平均状态空间模型的可控/可观Lyapunov 方程:

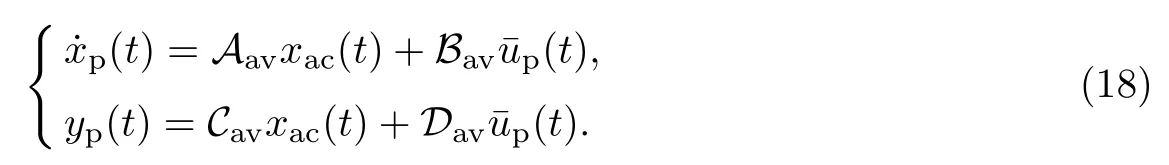
(2) 对矩阵进行Cholesky 分解:=.

(3) 对矩阵进行特征值分解:=, 其中Σav=diag{σav1,σav2,··· ,σavn}.

(4) 计算相应的坐标变换矩阵:Tav=.

(5) 通过坐标变换计算给定切换系统小信号交流平均模型以及各子系统模型的平衡实现:

(6) 根据待求解降阶模型阶数r对各平衡实现下的状态空间参数矩阵进行分块, 可得

式中:Aavb11∈Rr×r;Bavb1,,∈Rr×p;Cavb1,,∈Rm×r.进一步可根据下式

生成待求的降阶快周期切换系统模型参数矩阵, 其中0< α <1为可调参数, 通常选取为交流摄动信号与直流信号之比的估计值, ()为交流小信号平均模型(17)采用奇异摄动平衡截断所生成的降阶模型参数矩阵:

输出: 低阶线性切换系统模型(Ari,Bri,Cri,Dri).

定理2算法2 生成的降阶周期切换系统同样满足弱稳定性(即存在足够高的切换频率使得其稳定), 降阶周期切换系统的交流小信号平均模型与原周期切换系统的交流小信号平均模型(17)在全频域上的逼近性能存在下列H∞范数意义下的误差界:

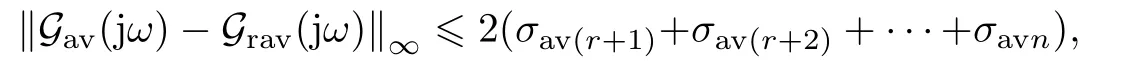
其中Grav(jω) =Crav(jωI −Arav)−1Brav+Drav为降阶周期切换系统交流小信号平均模型(Arav,Brav,Crav,Drav) 的传递函数.

证明 结合式(17)中关于交流小信号平均模型的定义以及算法2 中各降阶子系统模型参数的计算公式可得

进一步, 可以证明

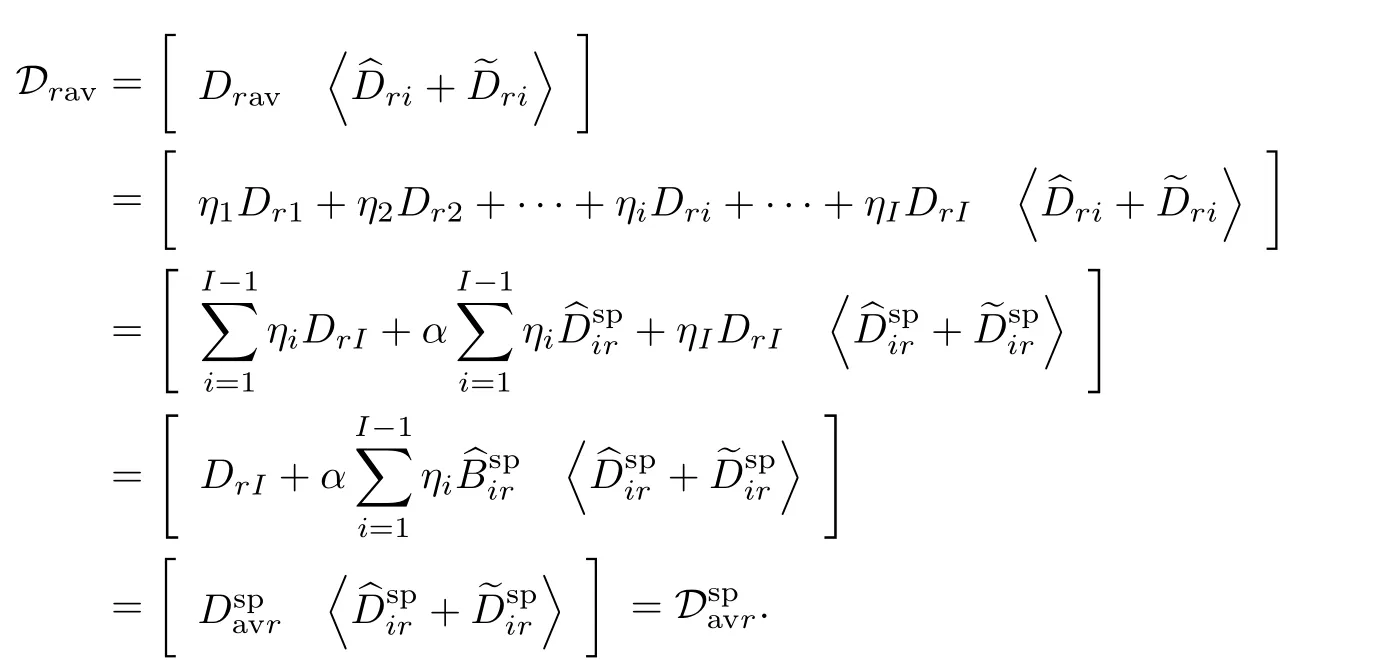
同样不难看出, 降阶周期切换系统的交流小信号平均模型Grav(jω)(Arav,Brav,Crav,Drav)与直接对原系统交流小信号平均模型(17)进行标准平衡截断模型降阶所得线性时不变模型(jω)()完全一致, 根据标准平衡截断理论可知为Hurwitz 矩阵满足

进一步根据引理1 可知, 降阶周期切换系统具有快切换条件下的弱稳定性, 同时其交流小信号模型满足全频域下的逼近误差性能:

注2与算法1 相同, 算法2 中同样采用奇异摄动型平衡截断来对首先生成平均模型的降阶系统参数; 但由于直流平均模型与交流小信号模型结构的不同, 算法2 中采用了与算法1 不同的方式来生成降阶周期切换子系统的模型参数, 但生成两类算法的初衷都在于使其降阶周期切换系统的平均模型与平均模型的降阶系统相匹配.

注3 周期切换系统作为一类特殊的切换系统, 采用针对一般切换系统开发的模型降阶方法[14,23-24]在理论上是可行的, 但这些方法均需假设各子系统必须为渐进稳定, 且求解算法涉及多组Lyapunov 或广义Lyapunov 方程, 甚至Lyapunov 矩阵不等式的求解.本工作中的两类算法中均不需要假设切换系统的子系统渐进稳定, 只要其平均模型稳定即可进行求解, 同时算法中仅涉及到一组Lyapunov 方程求解以及一些简单的矩阵运算, 可以更为方便地处理周期切换系统的模型降阶问题.

3 仿真算例

考虑Henry[37]给出的一个关于梯形拓扑结构下四级交换电容式直流对直流(DC-DC)转换器的建模案例, 其电路结构如图1 所示.

图1 梯形拓扑结构四级交换电容式转换器电路结构示意图Fig.1 Schematic diagram of four-stage SC converter with a ladder topology

图1 所示的10 个“开关/切换”元件为FDMS8460 MOSFETs, 其等效开关电阻用Rsw=0.003 表示, 8 个电容元件均为Nichicon 的陶瓷电容, 其电容值Cc= 25, 等效电阻为Rc=0.001.以各电容的两端电压作为状态,Vin,Vout2 个端口的电压信号作为系统的输入, 电容C1的两端电压信号作为系统的输出, 根据其开关元件的状态[37], 该切换电路的切换周期为0.50 s, 2 个切换模式即子系统的占空比均为0.5, 即各自在一个周期内的激活时间均为0.25 s.借助基尔霍夫电压电流定理对该电路进行分析建模, 可求得该电路在切换模式1 和2 下的状态空间方程为

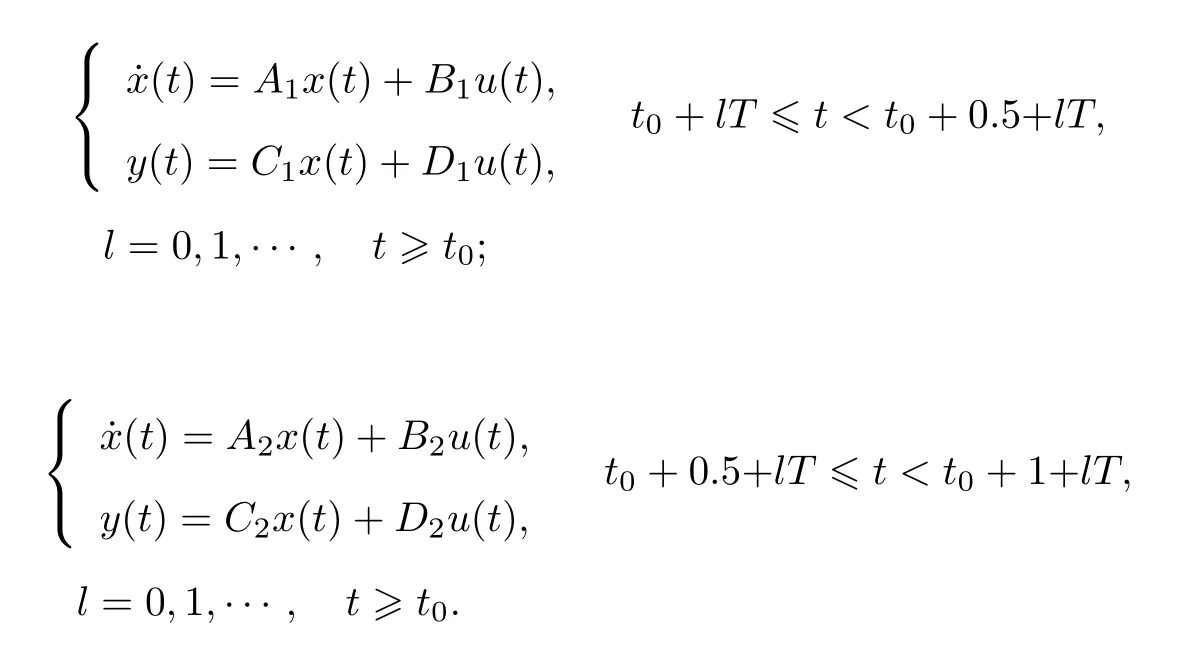
2 个切换模式下的子系统参数矩阵分别为

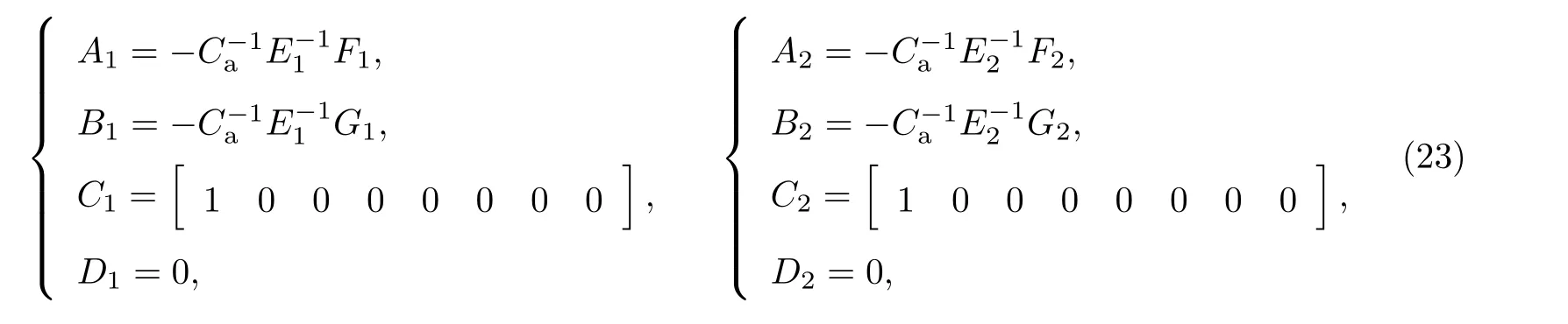
式中:Ca为由各电容的电容值组成的对角矩阵,Ca=diag{Cc,Cc,··· ,Cc};E1,F1,G1和E2,F2,G2包含了电路在2 个不同切换模式下的开关元件的状态信息以及其他参数信息, 分别为

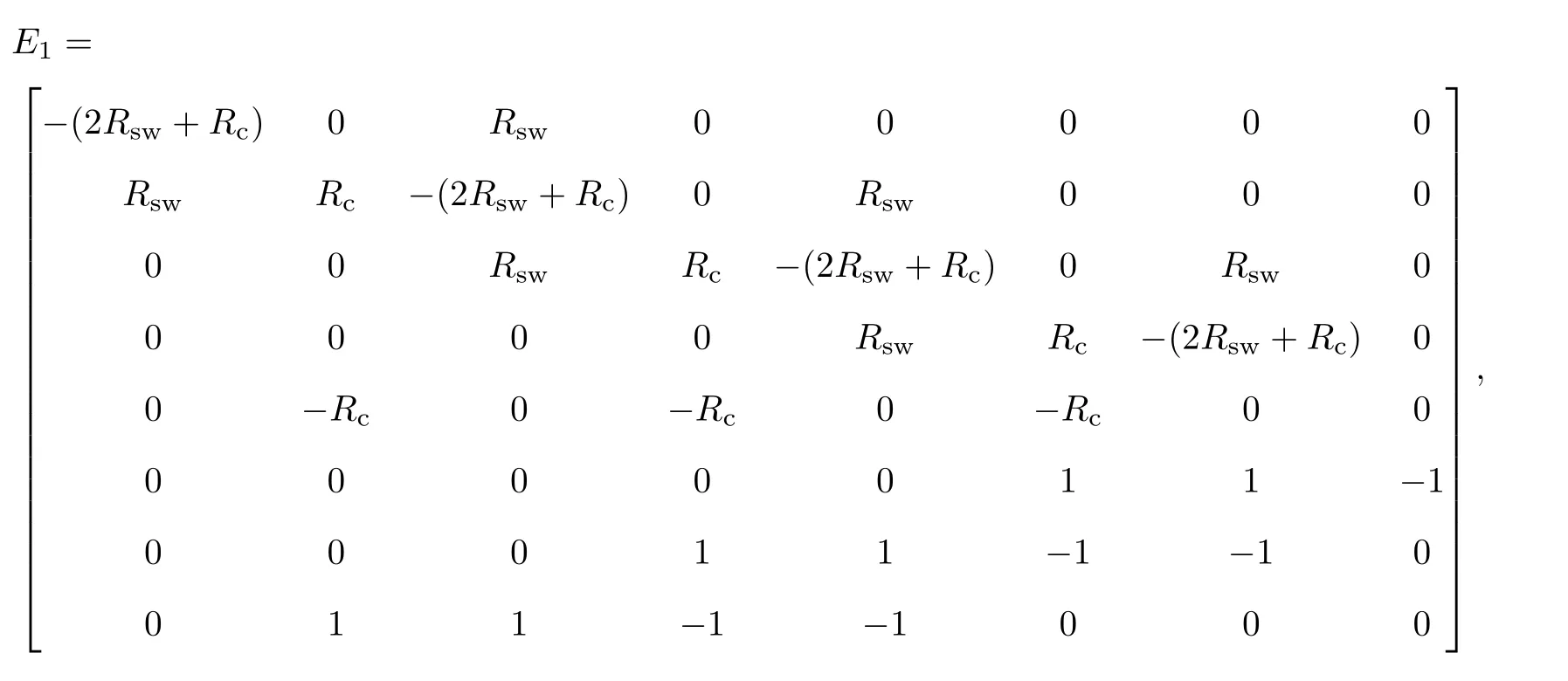
通过Matlab 计算不难发现, 上述电路的2 个切换子系统均存在虚轴上的极点, 无法直接应用Petreczky 等[14]提出的线性矩阵不等式方法来求解其共同格拉姆矩阵, 也无法直接应用Monshizadeh 等[23]给出的子系统格拉姆矩阵平均法进行求解.幸运的是, 该电路的直流平均模型/交流小信号平均模型中的平均状态矩阵Aav=Aav=0.5A1+0.5A2为Hurwitz 矩阵, 可直接应用本方法中的算法1 或算法2 进行求解.

(1) 首先考虑输入为直流信号的情况.设需要的降阶模型阶数为2, 则基于直流平均模型(5)通过算法1 生成2 阶的周期切换子系统模型参数矩阵:

为直观地展现降阶后的2 阶周期切换模型对原8 阶周期切换系统的逼近性能, 可以通过Matlab 进行仿真验证, 在仿真程序中输入如下直流信号:

图2 为仿真所得2 阶周期切换系统在直流输入下的输出信号.

图2 算法1 所得2 阶周期切换系统在直流输入下的逼近性能Fig.2 Approximation performance of the 2nd reduced switched systems obtained by using Algorithm 1 in the presence of DC input

从图2 可以看出, 在相同的(零频)直流输入信号激励下, 算法1 所得2 阶降阶周期切换模型对原8 阶周期切换系统具有良好的逼近效果, 相应的输出误差非常小, 充分说明了算法1 在直流输入情形下的有效性.同时, 2 个周期切换系统的直流平均模型所得输出误差收敛为0, 这与定理1 给出的理论分析结果相符.

(2) 考虑输入在直流信号之外存在交流摄动信号以及切换时间存在摄动的情况.同样假设所需降阶模型的阶数为2, 则基于交流小信号平均模型(17), 可应用算法2 得到相应的2 阶周期切换子系统模型参数矩阵:

令算法2 中的可调参数α=0.1, 即设交流摄动信号与直流信号之比的估计值约为0.1.该2 阶周期切换模型在存在交流摄动以及切换时间摄动情形下的逼近性能同样可通过Matlab 进行仿真验证.在直流信号的基础上增加交流摄动信号, 式(24)变换为

令切换时间的摄动值为

图3 为标准周期切换信号和带有切换时间摄动的周期切换信号.由图3 可知, 子系统1 在T=0.5 s 的切换周期中的激活时间由0.250 0 s 摄动为0.292 4 和0.207 6 s.

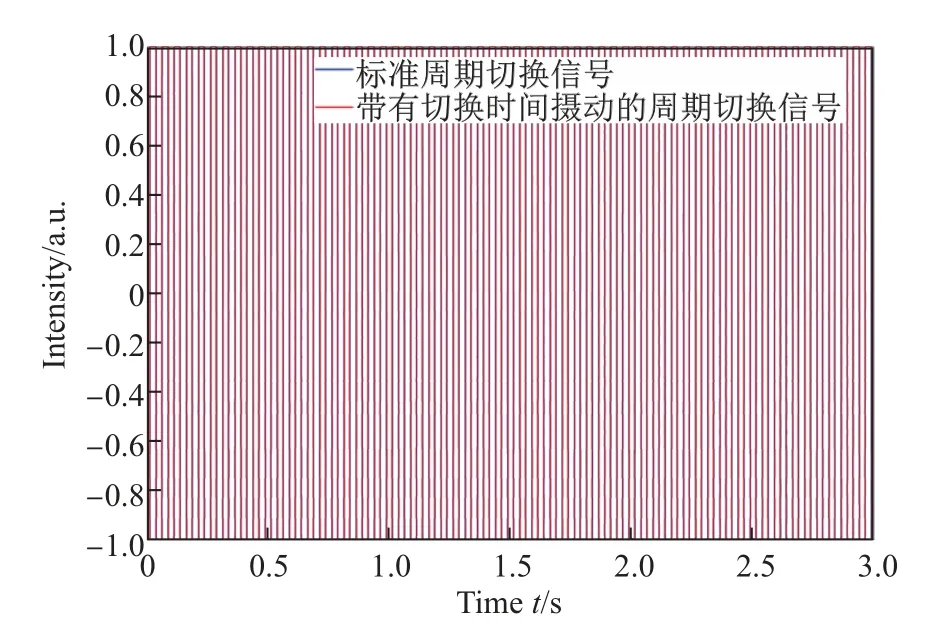
图3 标准周期切换信号与带有切换时间摄动的周期切换信号Fig.3 Periodically switching signal and perturbed periodically switching signal

为与算法1 中所得降阶模型进行比较, 图4 分别给出了通过算法2 以及算法1 分别得到的降阶周期切换模型与原模型之间逼近性能的曲线, 包括原8 阶周期切换系统与2 阶周期切换模型的输出曲线以及相应的输出误差曲线.

通过图4 可以看出, 相对于基于直流平均模型的降阶算法1, 采用基于交流小信号平均模型的算法2 所得到的2 阶降阶模型在带有交流摄动输入信号以及切换时间摄动的情形下有着更好的逼近性能.这进一步说明了在考虑交流摄动输入信号以及切换时间摄动的情况下设计算法2 的必要性.

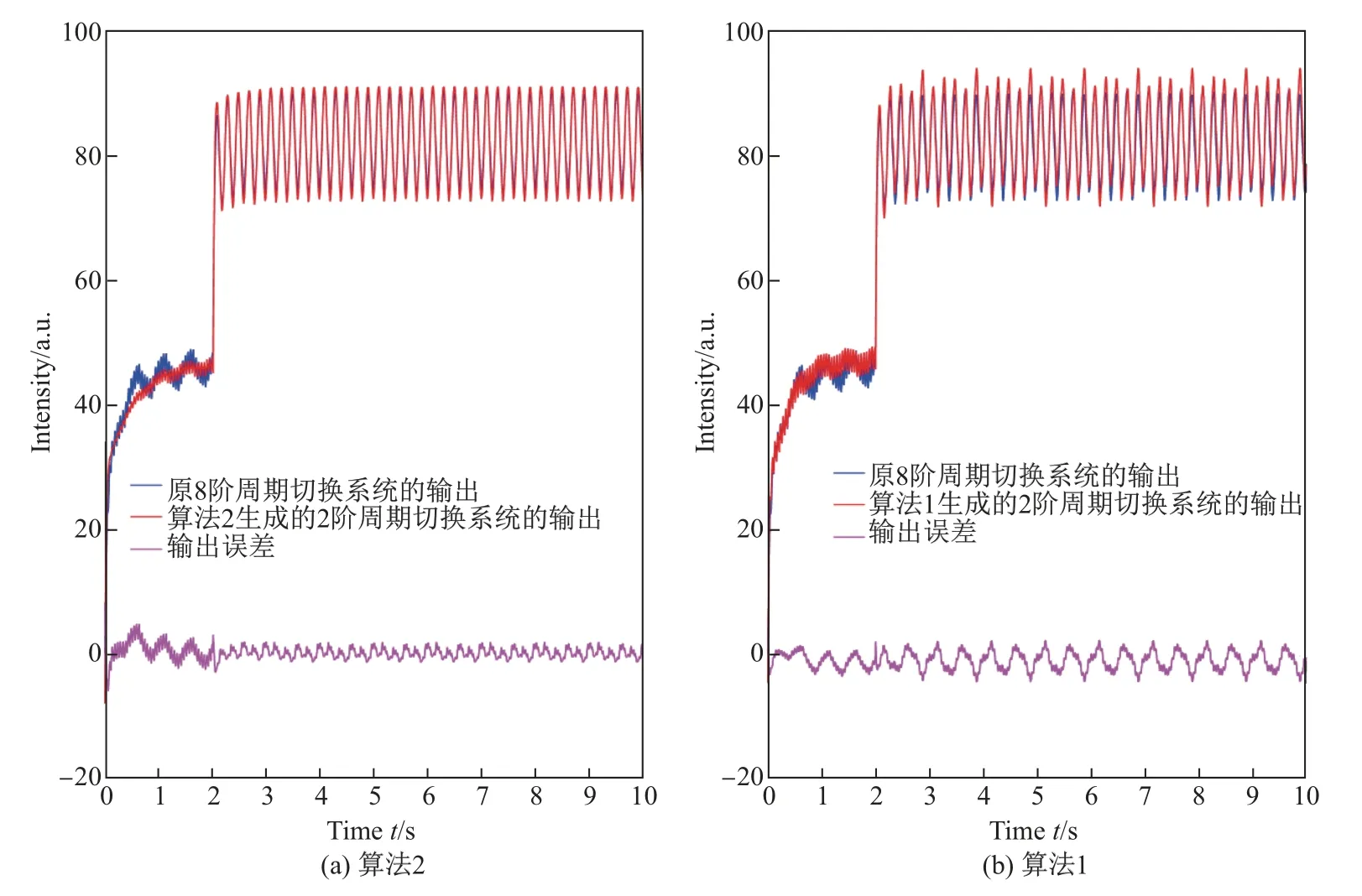
图4 2 阶周期切换系统在直流-交流输入以及切换时间摄动情形下的逼近性能Fig.4 Approximation performance of the 2nd reduced switched systems obtained by using Algorithm 2 and Algorithm 1 in the presence of DC-AC input as well as switched time perturbation

通过仿真算例可以得出, 算法1 非常适用于仅存在直流输入情形下的快周期切换系统模型降阶问题, 而对存在交流摄动输入信号以及切换时间摄动的快周期切换系统模型降阶问题,则可以考虑采用算法2 来求解相应的降阶周期切换系统模型参数矩阵.

4 结束语

针对快周期切换系统的模型降阶问题, 本工作通过引入其直流平均模型和交流小信号平均模型, 结合奇异摄动平衡截断理论分别给出了两类求解降阶周期切换模型参数矩阵的算法.这两类算法均可保持原系统在快周期切换下的稳定性, 同时可分别生成逼近系统在仅有直流输入以及存在交流摄动与切换时间摄动输入情形下输入输出相应特性的降阶模型.应用仿真例子验证了所提算法的有效性以及两类算法的不同适用范围.