ZHOU Bibo(周碧波)，ZHANG Lingling(张玲玲)，BAI Sang(白桑)

(1.College of Biomedical Engineering，Taiyuan University of Technology，Taiyuan 030024，China; 2.Department of Mathematics，Lvliang University，Lvliang 033000，China; 3.State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing 100081，China)

Abstract: In this paper，we are concerned with the existence and uniqueness of positive solutions for two kinds of nonlinear conformable fractional differential systems.By means of the fixed point theorems of sum-type operators and mixed monotone operators based on the cone theory，our results can not only guarantee the existence of a unique positive solution，but also be applied to construct an iterative scheme for approximating it.Finally，some examples are given to illustrate the main results.

Key words: Existence and uniqueness; Sum-type operator; Mixed monotone operator;Cone theory; Impulsive

1.Introduction

In the past decades，fractional c alculus and its potential applications have gained considerable popularity and importance，mainly because fractional calculus has become a powerful tool for the description of memory and heredity properties of various materials and processes.As fractional differential equation models are more realistic and practical than the classical integer order models，there are a large number of papers and monographs that deal with various phenomena of science and engineering in fractional calculus.For details，see[1-4]and the references therein.

Two types of fractional derivatives，namely Riemann-Liouville and Caputo，are very famous，many scholars have done a lot of researches on various problems of fractional differential equations based on these two definitions.Mathematicians prefer the Riemann-Liouville fractional derivative because it is amenable to many mathematical manipulations.In contrast，physicists and engineers prefer Caputo fractional derivative.Fractional differential equations is gradual to develop into an important subject in the mathematical analysis area.For more history and development，we refer to the monographs [8-9，13，18].

Recently，in [10]，Khalil defined a new fractional derivative called ”the conformable fractional derivative”.Compared with Riemann-Liouville and Caputo fractional derivative，this new definition is well-behaved and it just depends on the basic limit definition.Namely，for a function f :(0，∞)→R the conformable fraction derivative of order 0 ＜α ＜1 of f at t ＞0 was defined byand the fraction derivative at 0 is defined asThe new definition seems to be a natural extension of the usual integer derivative，and it satisfies the major properties of the integer derivative.In [12]，by using the definition of the new fractional derivative，the authors investigated the existence of solution for a class of initial value problems of conformable differential equation as follows:

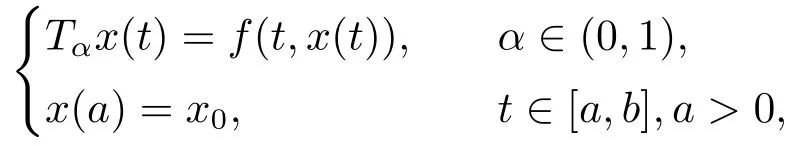
where f : [a，b] × R →R is a continuous function，and Tαx(t) denotes the conformable fractional derivative of x at t of order α.For the fist time in the literature of conformable fractional calculus，the authors introduce the notion of tube solution.

Batarfi et al.[16]investigated the three-point boundary value problems for a class of conformable fractional differential equations

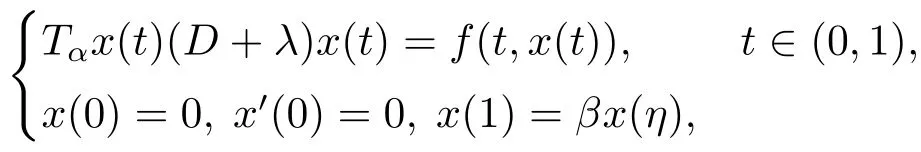
where Tαis the conformable fractional derivative operator of order α ∈(1，2]，D is the ordinary derivative operator，f : [0，1]×R →R is a known continuous function，λ and β are all real numbers.By means of the fixed-point theorem in cone，some existence results of linear system and nonlinear system are obtained.

In [17]，the authors studied the following boundary value problem of nonlinear fractional differential equation with p-Laplacian operator:

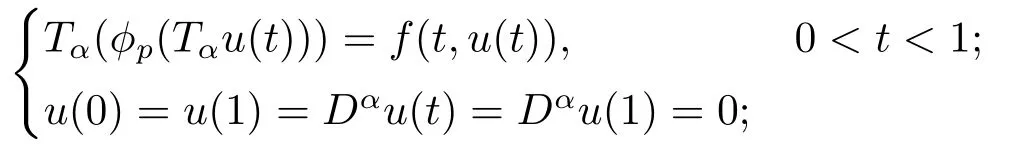
where 1 ＜α ＜2 is a real number，φpis p-Laplacian operator and φp(s) = |s|p-2s，Tαis the conformable fractional derivative operator.By the use of an approximation method and fixed point theorems on cone，some existence and multiplicity results of positive solutions were acquired.

Motivated and inspired by the above research work，we are concerned with conformable fractional differential equations as follows:

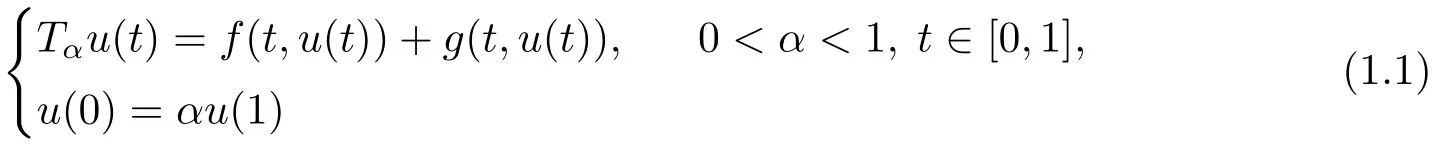
and

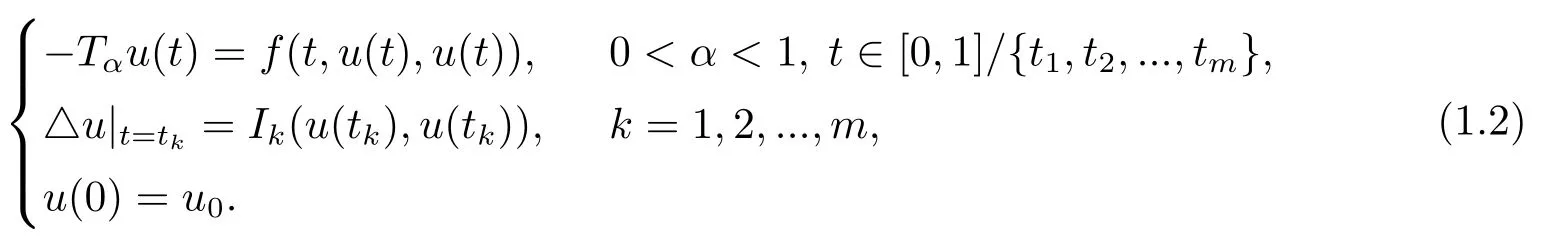
For the system(1.1)，by using sum-type operator methods，we examine the existence-uniqueness and the monotone iterative sequence of positive solutions.For the system (1.2) with impulsive terms，by using mixed monotone fixed point theorem，we investigate the existence and uniqueness of positive solution.Our result can not only guarantee the existence of unique positive solution，but also be applied to construct an iterative scheme for approximating it.

2.Preliminaries

In this section，we list some basic notations，definitions in ordered Banach spaces.For the convenience of the reader，we refer to [5-6，19] for details.

A nonempty closed convex set P ⊂E is a cone if it satisfies:

(I1) x ∈P，λ ≥0 ⇒λx ∈P;

(I2) x ∈P，-x ∈P ⇒x=θ.

Suppose that(E，‖·‖)is a real Banach space which is partially ordered by a cone P ⊂E，that is x ≤y if and only if y-x ∈P.If x ≤y and xy，then we denote x ＜y or y ＞x.By θ we denote the zero element of E.

For all the x，y ∈E，the notation x ～y meas that there exists λ ＞0 and µ ＞0 such that λx ≥y ≥µx.Clearly ～is a equivalence relation.Giving h ＞θ，we denote by Phthe set Ph={x ∈E |x ～h}.It is easy to see that Ph⊂P is convex and λPh=Phfor all λ ＞0.Ifθ and h ∈，it is clear that Ph=P.

Definition 2.1[11]The conformable fractional derivative staring from a of a function f :[a，∞)→R of order 0 ＜α ＜1 is defined by

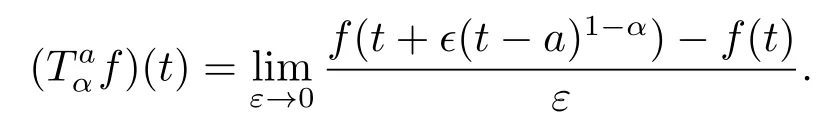
When a=0 we write Tα，if the α order conformable fractional derivative exists，then we say f is α-differentiable.

Definition 2.2[11]The conformable fractional integral staring from a of a function f :[a，∞)→R is defined by

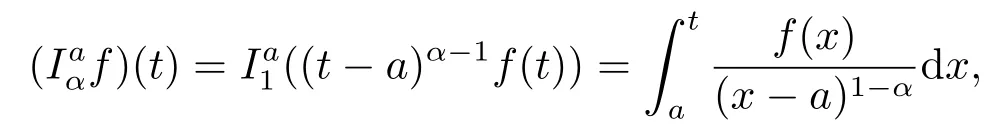
when integral is the usual Riemann improper integral，and α ∈(0，1).

Definition 2.3[15]Let D = P，or D =and γ be a real number with 0 ≤γ ＜1.An operator A:P →P is said to be γ-concave if it satisfies

Definition 2.4[17]An operator A:P →P is said to be sub-homogeneous if it satisfies

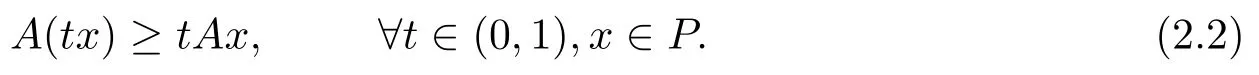
Definition 2.5[14]A : P ×P →P is said to be a mixed monotone operator if A(x，y)is increasing in x and decreasing in y，that is，u1，v1，u2，v2∈P and u1＜u2，v1＞v2，implies that A(u1，v1)≤A(u2，v2).Element x ∈P is called a fixed point of A if A(x，x)=x.

Lemma 2.1[15]Let P be a normal cone，A : P →P be an increasing operator and B :P →P be a decreasing operator.Assume that

(I) For any x ∈P and t ∈(0，1)，there exist φi(t)∈(t，1)(i=1，2) such that

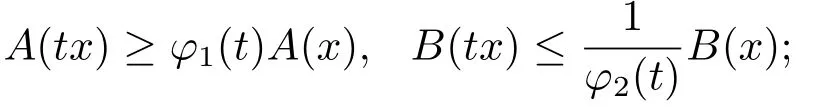
(II) There exists h0∈Phsuch that Ah0+Bh0∈Ph.

Then，

1) There exist u0，v0∈Phand r ∈(0，1) such that

rv0≤u0＜v0，u0≤Au0+Bv0≤Av0+Bu0≤v0;

2) The operator equation Ax+Bx=x has a unique solution x*in Ph;

3) For any initial values x0，y0∈Ph，constructing successively the sequences

xn=Axn-1+Bnn-1，yn=Ayn-1+Bxn-1，n=1，2，···，

we have xn→x*and yn→x*as n →∞.

Lemma 2.2[9]A : P ×P →P is a mixed monotone operator，for ∀γ ∈(0，1)，there exist a function φ(γ)∈(γ，1) such that

A(tx，t-1y)≥φ(γ)A(x，y)，t ∈(0，1)，x，y ∈P.

Assume that there exist h ∈P such that A(h，h)∈Ph.Then，

1) A:Ph×Ph→Ph;

2) There exist u0，v0∈Phand r ∈(0，1) such that

rv0≤u0＜v0，u0≤A(u0，v0)≤A(v0，u0)≤v0;

3) The operator equation A(x，x)=x has a unique solution x*in Ph;

4) For any initial values x0，y0∈Ph，constructing successively the sequences

xn=A(xn-1，yn-1)，yn=A(yn-1，xn-1)，n=1，2，···，

we have xn→x*and yn→x*as n →∞.

3.Bound Value Problems

Lemma 3.1Let f，g ∈C[(0，1)×R+，R+].Then u ∈C[0，1] is a solution to (1.1) if and only if u is the solution to the following integral equation:

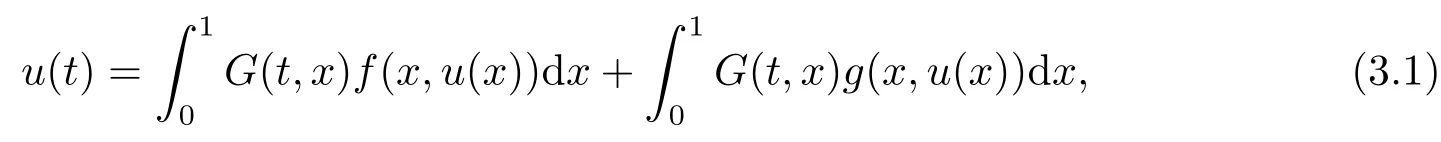
where

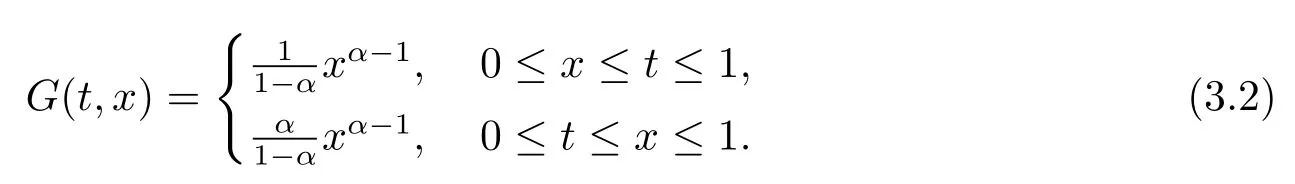
ProofLet P = {u | u(t) ≥0，∀t ∈[0，1]} and u(t) is a solution of conformable fractional differential equation (1.1).We integrate the both sides of equation (1.1)，so we have the following results

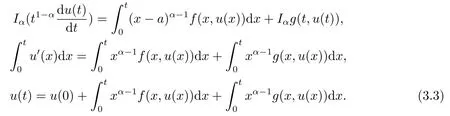
Letting t=1，by (1.1) and (3.3) we can know

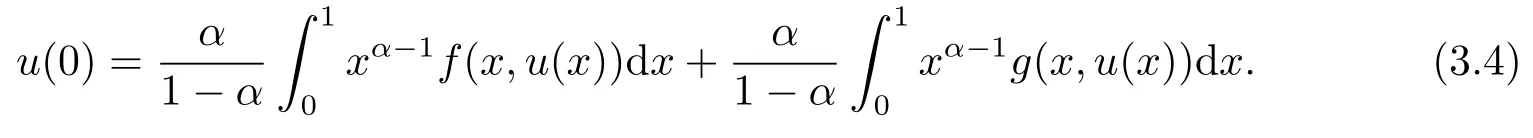
We can get the following equation by combining (3.3) and (3.4).

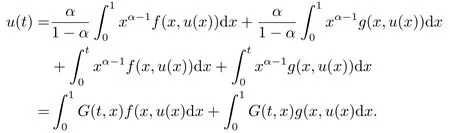
The proof is complete.

Theorem 3.1Assume that f(t，u(t))+g(t，u(t))0 and

(H1) f，g : [0，1]×[0，+∞) →[0，+∞) is continuous，f(t，u) is increasing and g(t，u) is decreasing in u ∈[0，+∞) for fixed t ∈[0，1];

(H2) For any x ∈P and t*∈(0，1)，there exist φi(t*)∈(t*，1)(i=1，2) such that

Then the equation(1.1)has a unique positive solution u*.Moreover，for any initial value u0，v0∈Ph，constructing successively the following sequences，

we have un(t)→x*(t) and vn(t)→x*(t) as n →+∞.

ProofLet

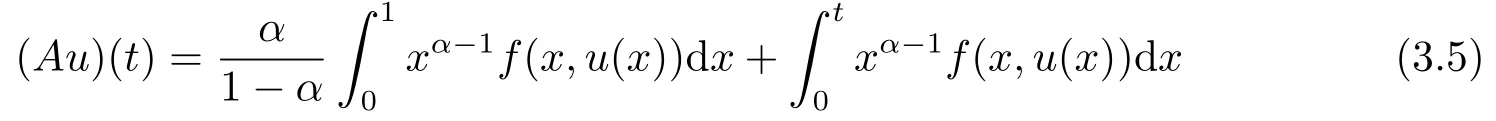
and

It is easy to know that A : P →P is an increasing operator and B : P →P is a decreasing operator by the condition(H1)，(3.5)and(3.6).We know that the equation(1.1)is equivalence to sum operator equation Au+Bu=u by Lemma 3.1.

Step 1 We prove A(t*u)≥φ1(t*)Au andBu.

By the condition (H2) of Theorem 3.1，we can know

Step 2 We prove there exist h0∈Phsuch that Ah0+Bh0∈Ph.

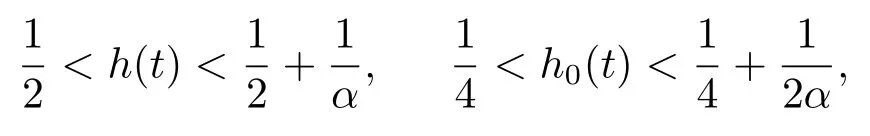
and

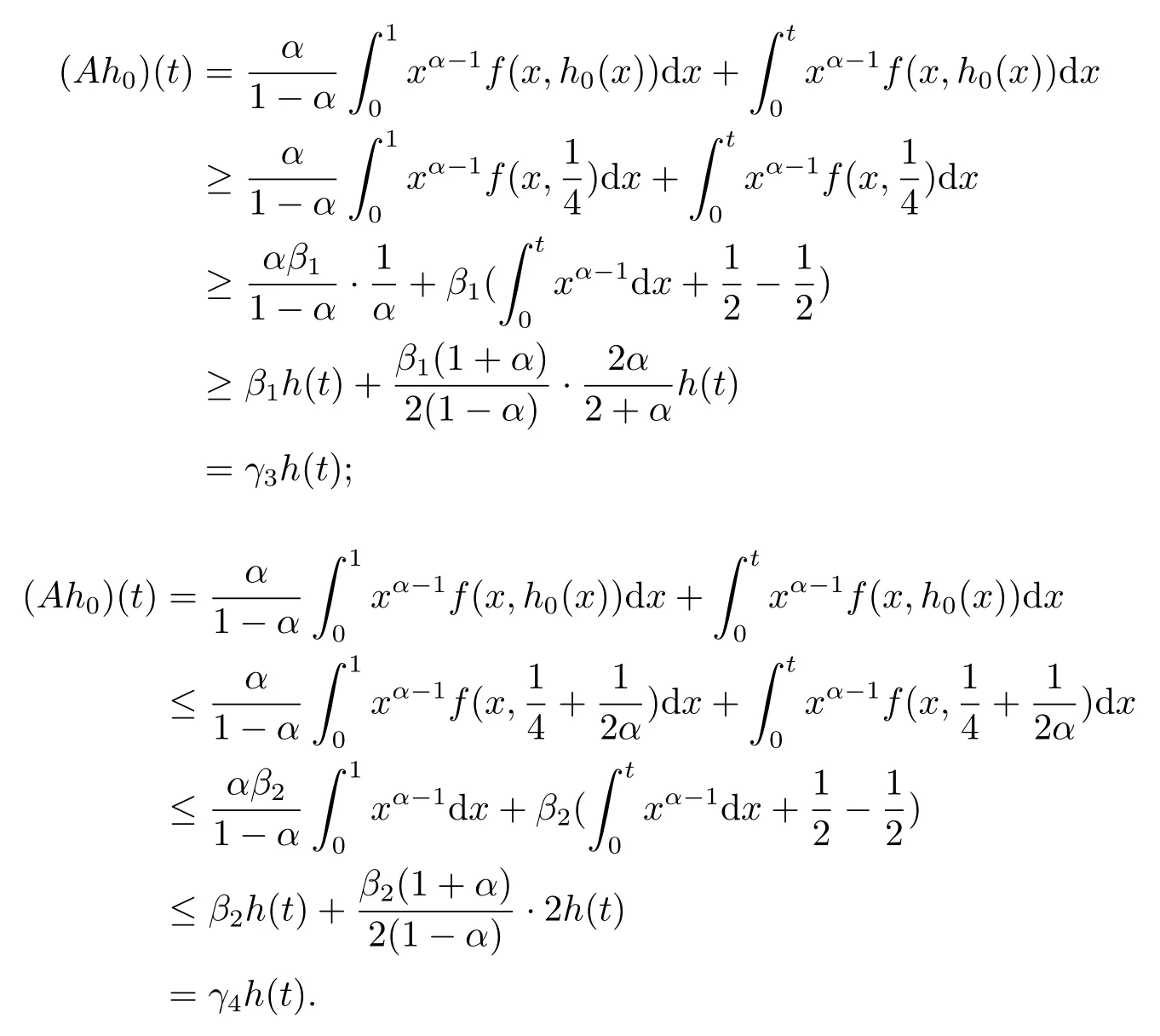
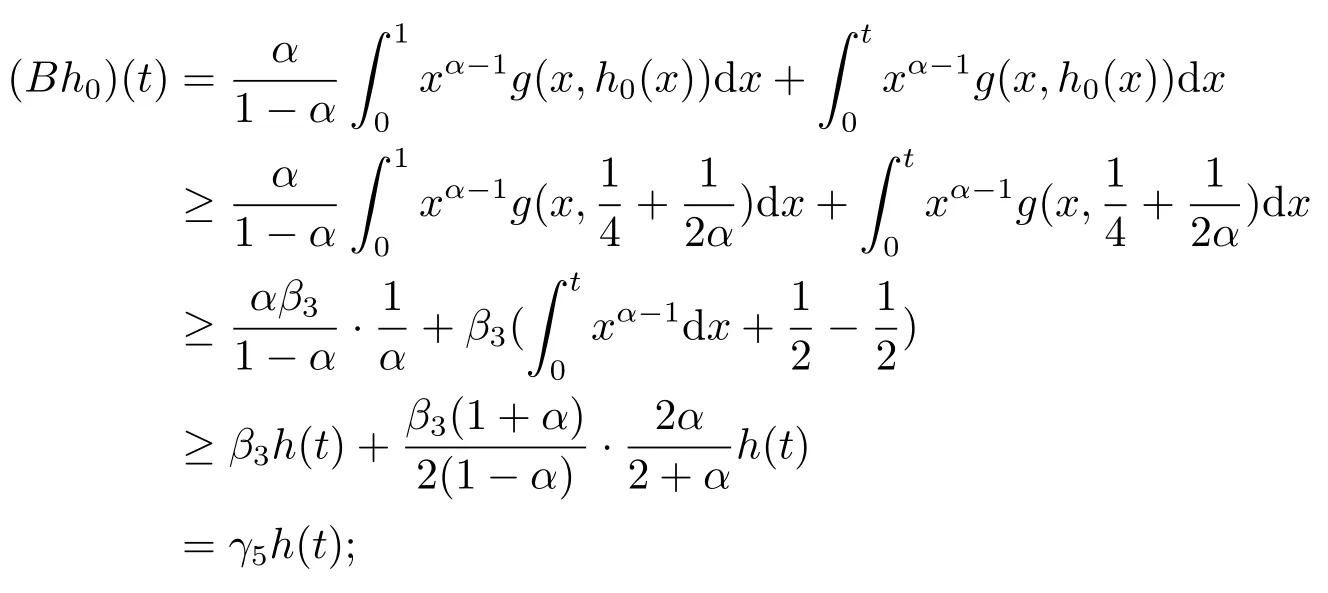
From the above conclusion we can get

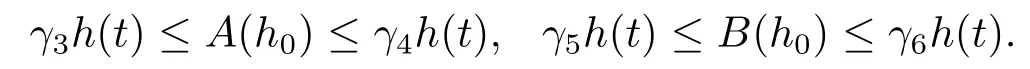
It means that(γ3+γ5)h ≤A(h0)+B(h0)≤(γ4+γ6)h，that is，(A+B)(h0)∈Ph.According to Lemma 2.1，we know that the operator equation Au+Bu=u has a unique positive solution x*in Ph，and there exist u0，v0∈Phand γ ∈(0，1) such that

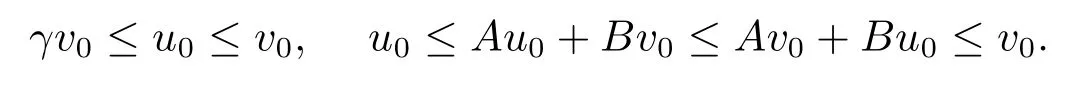
And for any initial value u0，v0∈Ph，constructing successively the sequences

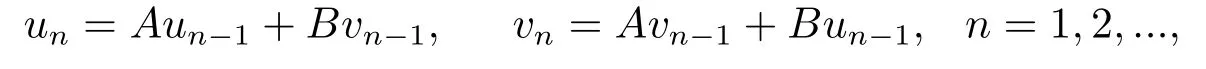
we have un→u*，vn→u*as n →∞.

Corollary 3.1Assume that

(H1)′f : [a，b]×[0，+∞] →[0，+∞] is continuous and increasing with respect to the second argument，f(t，0)0;

(H2)′for any x ∈P and t ∈(0，1)，there exist φ3(t) ∈(t，1) such that f(x，tu) ≥φ3(t)f(x，u).

Then the problem

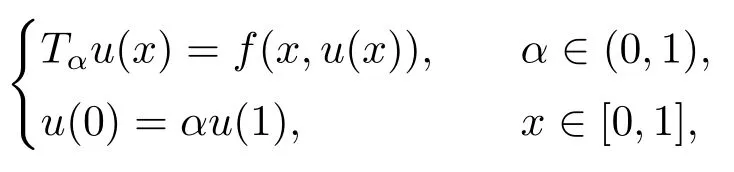
has a unique positive solution u*.Moreover，for any initial value u0∈Ph，constructing successively the sequence

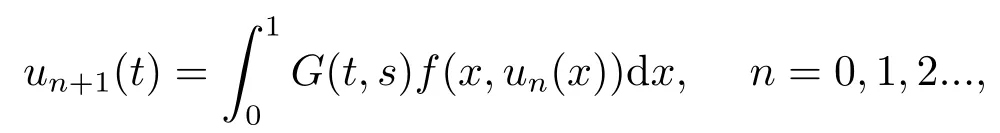
we have un(t)→u*(t) as n →+∞.

4.Initial Value Problems with Impulsive Terms

Throughout this subsection，we use the following notation.

Let J =[0，1]，R+=(0，∞)，f ∈[J ×R+×R+，R+]，0 ＜t1＜t2＜...＜tm＜1.△u|t=tkdenotes the jump of u(t) at t = tk，and Δu|t=tk= u()-u()，where u() and u()represent the right and left limits of u(t) at t = tk，respectively.Also，Ikis a given function in C[R+×R+，R+].

Let PC[J，R] := {x | x : J →R，x(t) is continuous at ttk，and left continuous at t = tk，x() exists，k = 1，2，...m}.Then，we can easily find that PC[J，R] is a Banach s pace with norm

Lemma 4.1Let f ∈C[J ×R+×R+，R-]，then u ∈PC[J，R]∩C1[J′，R] is a solution to (1.2) on J if and only if u ∈PC[J，R] is the solution to the following integral equation:

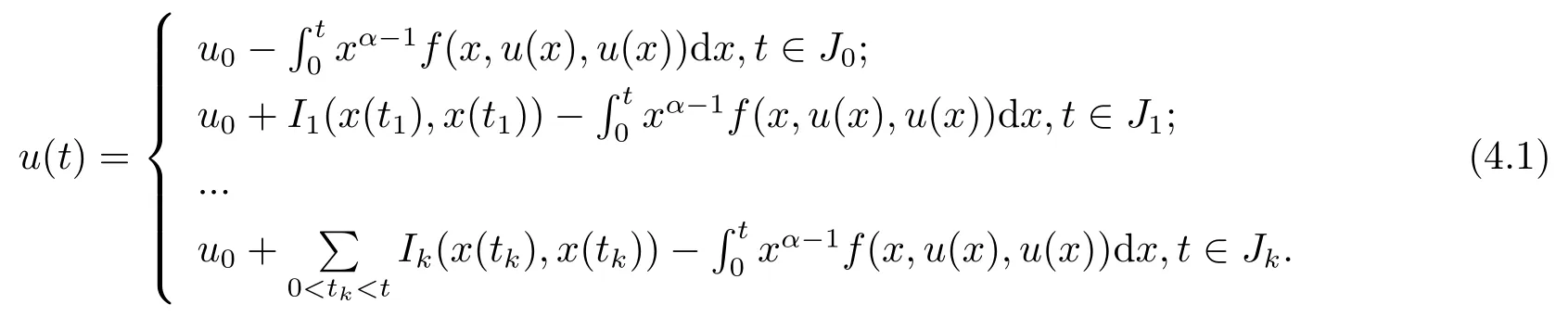
ProofIf t ∈J0，we take α time integral for the first equation on both of (1.2)，the following contents can be obtained，

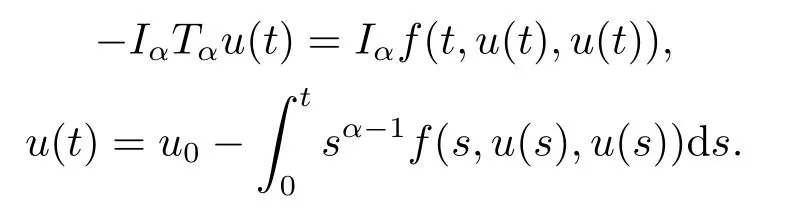
If t ∈J1，we take α time integral for the first equation on both of(1.2)，then the following contents can be obtained，

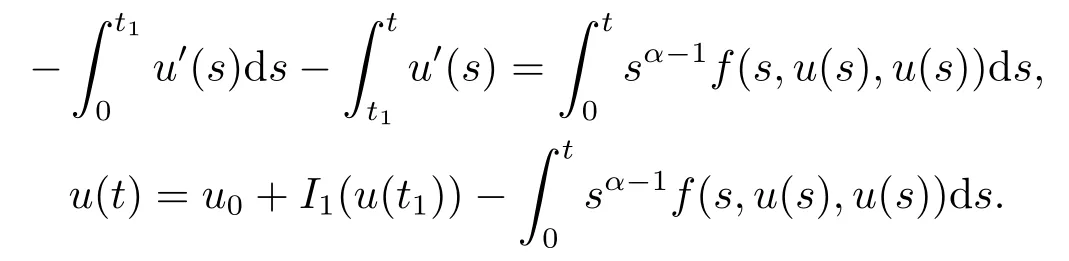
If t ∈Jk，the following conclusions can be obtained，

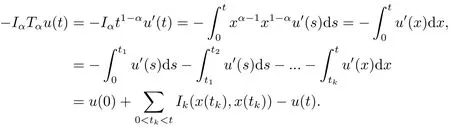
So we get，

Then，we can know the integral form solution (1.2) is (4.1).

Now let’s go on to prove (4.1) to meet the various equations of (1.2).

If t ∈J0，let t=0，by (4.1) we can know that u(0)=u0.

If t ∈J1，we take a α time conformable derivative on both sides of (4.1):

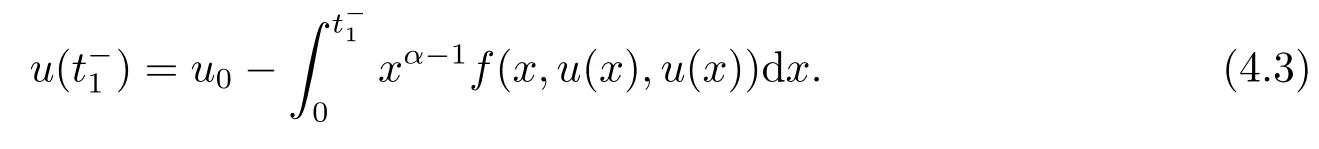
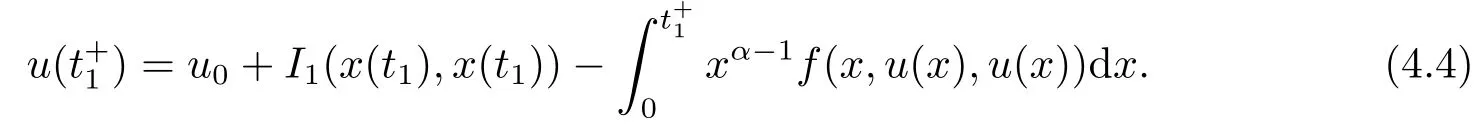
By subtracting the two equations in (4.3) and (4.4) ，then we can obtain

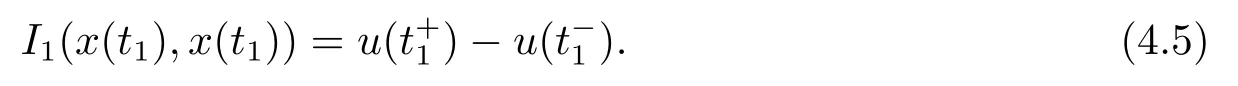
So it is to know，when t ∈J1，(4.1) meets all kinds of (1.2).In the same way，when t ∈Jk，we can prove that (4.1) meet all kinds of (1.2) too.That is (4.1) and (1.2) is completely equivalent，the proof is completed.

Theorem 4.1Assume that

(H3)f :J×R+×R+→(-∞，0]for all t ∈J and x，y ∈R+，also f(t，x，y)is nonincreasing in x for each t ∈J and y ∈R+and is nondecreasing in y for each t ∈J and x ∈R+.Moreover，＜0 for all t ∈J.

(H4) For each k =1，2，...，m，Ik:R+×R+→R+.Ik(x，y) is nondecreasing in x for each y ∈R+and is nonincreasing in y for each x ∈R+.

(H5) For all γ ∈(0，1)，there exist φ1(γ)，φ2(γ)∈(γ，1) such that

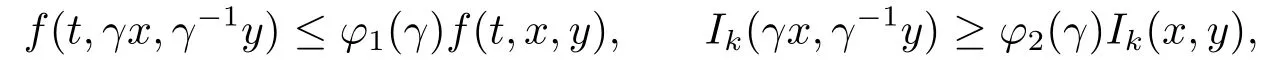
for any x，y ∈R+，and any k =1，2，...，m.

Then，there exists a unique positive solution x*to (1.2) on J.Moreover for any initial x0，y0∈Ph，constructing successively the following sequences，

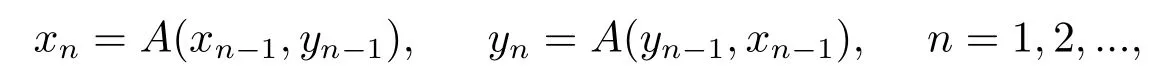
we have xn→x*and yn→x*as n →+∞.

ProofIn order to show the existence-uniqueness of the solution to (1.2)，we define an operator A:PC[J，R]×PC[J，R]→PC[J，R] by

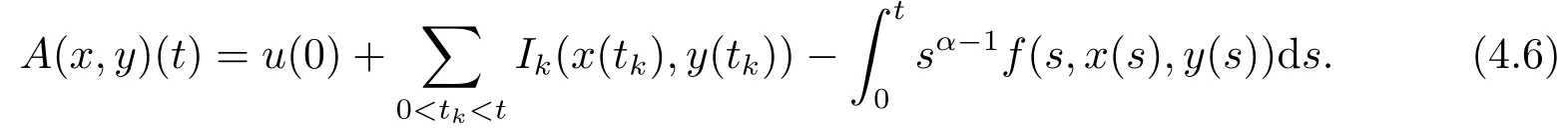
Then，we infer from (H3)，(H4) and (4.6) that

Step 1 We show there exist φ(γ) ∈(γ，1] such that A(γu，γ-1v) ≥φ(γ)A(u，v) for any u，v ∈P and γ ∈(0，1).

Put φ(γ) = min{φ1(γ)，φ2(γ)}，γ ∈(0，1).Then we see from (H5) that φ(γ) ∈(γ，1).Therefor for any γ ∈(0，1) and x，y ∈，from (H3)，(H4) and (H5)，we have

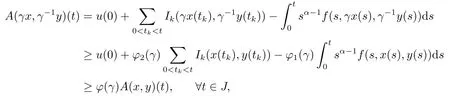
which implies that A(γx，γ-1y)(t)≥φ(γ)A(x，y)(t)，∀x，y ∈，γ ∈(0，1).

Step 2 We prove there exist h ∈P with hθ such that A(h，h)∈Ph.

Set a function h by

Then，we can easily obtain that∀t ∈J.Let

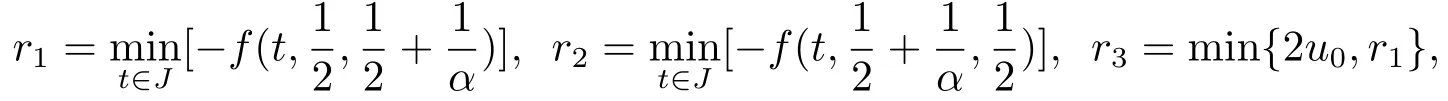
then，0 ≤r1≤r2.From (H3)，(H4) and (4.8)，it follows that

Also，we have

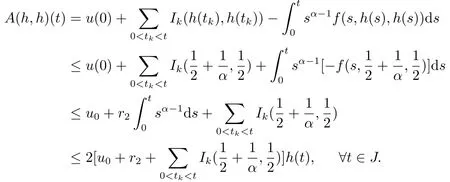
Thus，we observe that

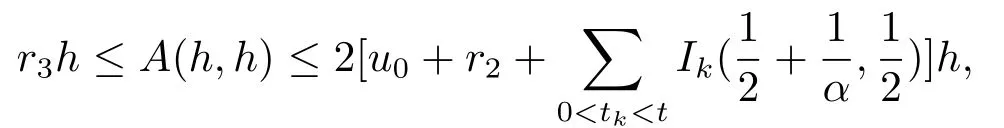
which implies that A(h，h)∈Ph.

By argument as above，we see that the operator A:×→defined by (4.6) satisfies all conditions of Lemma 2.2.Therefore，we conclude that the operator A has a unique fixed point in，hence there exist a unique positive solution to(1.2)on J.Moreover for any initial x0，y0∈，constructing successively the sequences

xn=A(xn-1，yn-1)，yn=A(yn-1，xn-1)，n=1，2，...，

one has ‖xn-x*‖→0 and ‖yn-x*‖→0 as n →∞.

Corollary 4.1Assume that (H3)，(H4) hold and

(H5)′Let α1，α2∈(0，1)，for all γ ∈(0，1).There exist γα1，γα2∈(γ，1) such that

f(t，γx，γ-1y)≤γα1f(t，x，y)，Ik(γx，γ-1y)≥γα2Ik(x，y)，

for any x，y ∈R+，and any k =1，2，...，m.

Then，there exists a unique positive solution x*to (1.2) on J，Moreover for any initial x0，y0∈Ph，constructing successively the sequences

xn=A(xn-1，yn-1)，yn=A(yn-1，xn-1)，n=1，2，...，

one has ‖xn-x*‖→0 and ‖yn-x*‖→0 as n →∞.

ProofLet φ1(γ)=γα1and φ2(γ)=γα2.We can get the above conclusion by Theorem 3.2.

5.Applications

As applications，two examples are presented to illustrate our main results.

Example 5.1

Conclusion 5.1The boundary value problem (5.1) has a unique positive solution in Ph，where

ProofIn this example，we haveLet

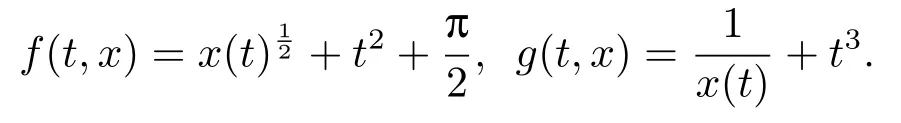
Obviously，f，g :[0，1]×[0，+∞)→[0，+∞) are continuous，f(t，x) is increasing and g(t，x) is decreasing in x ∈[0，+∞) for fixed t ∈[0，1].Beside，for λ ∈(0，1)，t ∈(0，1)，x ∈[0，+∞)，letting φ1(λ)=φ2(λ)=λ，we have

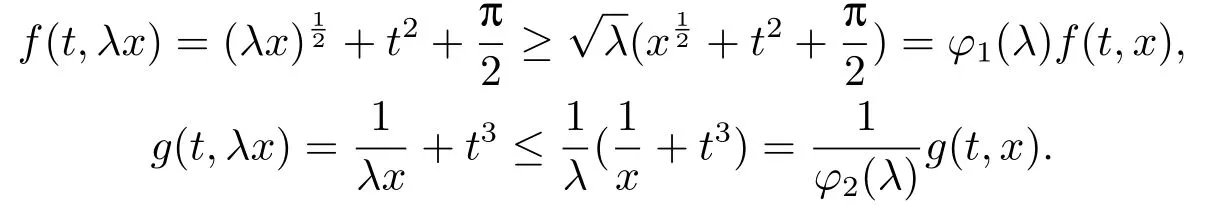
Hence all the conditions of Theorem 3.1 are satisfied.An application of Theorem 3.1 implies that the problem (5.1) has a unique positive solution in Ph.

Example 5.2

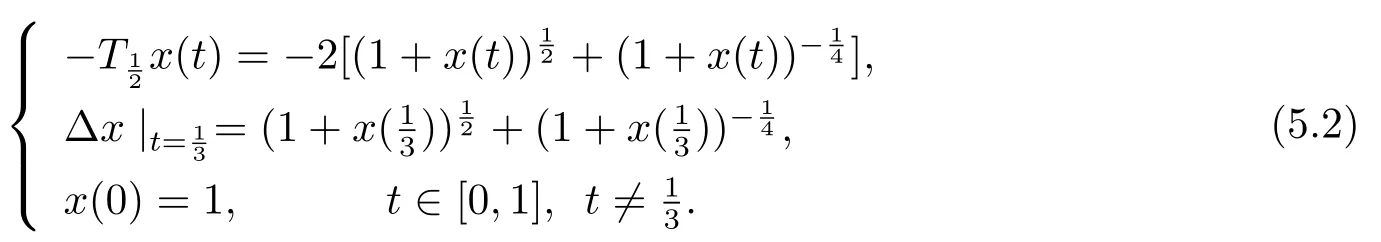
Conclusion 5.2The initial value problem for conformable fraction differential equations systems (5.2) with impulsive terms admits a unique positive solution in Ph，where h(t) =and the unique positive is continuously differentiable on

ProofLet J = [0，1]，f(x，y) = -2(1 + x(t))- 2(1 + y(t))Clearly，f(t，x，y) is decreasing in x for y ≥0 and increasing in y for x ≥0.Also，let I1(x，y) =(1+x(t))+(1+y(t))-and we know I1(x，y) is increasing in x for y ＞0 and is decreasing in y for x ≥0.

f(t，γx，γ-1y)=-2(1+γx(t))-2(1+γy(t))-≤φ(γ)f(t，x(t)，y(t))，∀x(t)＞0，y(t)＞0，

I1(γx，γ-1y)=(1+γx(t))+(1+γy(t))-≥φ(γ)I1(x(t)，y(t))，∀x(t)＞0，y(t)＞0.

Therefore，we see that condition (H3)，(H4) and (H5) hold.Hence，applying Theorem 4.1 to (5.2)，we can get a unique positive solution to (5.2) on [0，1].