姜 玫，马昌社

(华南师范大学计算机学院，广州 510631)

多重签名[1]允许一组签名者联合对同一消息进行签名，生成一个压缩的多重签名且验证者只需验证最终签名便可确认多个签名者对同一消息进行了签名[2]. 自1983年ITAKURA和NAKAMURA[1]提出多重签名的概念以来，多重签名的方案设计得到了充分研究，这些方案的安全性可归约于大整数分解问题[3-4]、离散对数问题[5-7]及格上困难问题[8]. 多重签名应用广泛，适用于电子合同、文件签署、电子商务和电子政务等众多领域[9].

2008年，BAGHERZANDI等[6]提出了基于离散对数的两轮多重签名BCJ方案，并在公钥验证模型下证明方案的安全性；2010年，MA等[7]提出了可在普通公钥模型下证明安全的两轮多重签名MWLD方案，其安全性可归约为求解离散对数问题；2016年，SYTA等[10]提出了具有较好扩展性的两轮多重签名CoSi方案，并认为该方案的安全性可归约为求解离散对数的困难性，但未给出方案的形式化安全证明；2018年，MAXWELL等[11]提出了第一个支持公钥聚合功能的两轮多重签名MuSig方案，并在普通公钥模型下证明方案的安全性.

然而，DRIJVERS等[12]指出BCJ方案[6]、MWLD方案[7]、CoSi方案[10]以及MuSig方案[11]存在的安全缺陷，并依次针对这4个方案的安全漏洞进行了亚指数时间攻击；同时，基于BCJ方案，提出了首个可形式化证明安全且只需2轮通信的mBCJ方案，其安全性可归约于求解离散对数的困难性. mBCJ方案采用了具有二义性的同态承诺，其中同态承诺可实现MS-BN方案[5]中前2轮通信的效果，进一步降低多重签名方案的通信代价；二义性的同态承诺能够有效避免伪造者从归约中抽取签名私钥，从而求解离散对数问题的具体实例，保证了mBCJ方案的安全性. 然而，基于离散对数问题构造的方案不能抵抗量子攻击，因此，mBCJ方案不适用于量子时代多方合作签名场景.

基于格上困难问题构造的方案能够抵抗量子攻击，满足了人们对方案安全性的最新需求. 在构造格上两轮多重签名方案时，本可沿用与mBCJ方案相似的构造思路——以普通Schnorr签名为基础，结合二义性同态承诺实现格上两轮多重签名，然而，通过分析格上困难问题与离散对数问题的不同之处，发现构造格上多重签名方案时，直接选用同态承诺可节省方案的通信量和计算量.

因此，本文以GLP签名[13]为基础，结合格上高效同态承诺[14]，在多项式环上设计了一个支持公钥聚合[11]功能的两轮多重签名方案(TLMS方案)，并在随机预言机模型中证明该方案的安全性.

1 预备知识

1.1 符号说明

N表示一个正整数且为2的方幂，q表示一个素数；表示多项式环[x]/(xN+1)，q表示多项式环q[x]/(xN+1)，q中环元素为N-1阶多项式且每一项系数属于[-(q-1)/2,(q-1)/2]，d表示q的子集且每一项系数属于[-d,d]，其中d+. 文中所有向量均为列向量，vΤ表示向量v的转置；分别表示向量v的1-范数、2-范数、无穷范数. 对于正整数η，η表示中无穷范数至多为η的多项式集合. 假设A表示集合，表示从A中均匀随机抽取元素a. 参考文献表示阶为N-1且32项系数为±1、其余项系数为0的多项式集合. 参考文献[14]，以特殊方式选择参数q，使得q中范数小的元素可逆；挑战空间为+}，差集为}.

1.2 困难问题及引理

问题2[16](Ring-SISm,q,β问题)给定m个多项式组成的向量a=(a1,a2,…,am)Τ要求找到一个非零向量x=(x1,x2,…,xm)m，使其满足且

引理1[17]选择参数N≥p≥1且为2的方幂，参数q为素数且满足q=2p+1(mod 4p)，则多项式xN+1可分解为环中p个不可约多项式的乘积，且对于多项式环q中任意非零环元素y，若y的范数满足或者则y存在逆元.

1.3 多重签名及其安全性

假设一组签名者L={1,2,…,l}将对消息m进行多重签名. 一般地，多重签名方案MS=(MKeyGen,MSign,MVerify)由以下3个算法组成：

(1)MKeyGen：密钥生成算法，给定安全参数θ，该概率算法为每位签名者i生成签名私钥ski和验证公钥pki；

(2)MSign：多重签名生成算法，输入公钥集合PK={pk1,pk2,…,pkl}和消息m，若签名成功,则该概率算法返回多重签名σ，否则返回⊥；

(3)MVerify：多重签名验证算法，输入待验证签名σ、消息m和公钥集合PK={pk1,pk2,…,pkl}，若待验证签名有效,则该确定性算法返回1，否则返回0.

参照文献[18]，下面给出多重签名方案的安全定义.

定义1(安全定义)多重签名方案MS=(MKeyGen,MSign,MVerify)是EUF-CMA安全的，若任意概率多项式时间的伪造者在以下游戏中获胜的概率可忽略不计：

step 1：挑战者输入安全参数θ并执行密钥生成算法，产生签名密钥对(sk,pk)，且向伪造者发送验证公钥pk；

step 2：伪造者自适应地发起消息mi(1≤i≤q)的签名查询，挑战者执行签名生成算法产生签名σi并发送给伪造者；

step 3：伪造者利用签名σi(1≤i≤q)，伪造一个新消息m*的签名σ*，若签名σ*有效，则伪造者在游戏中获胜.

1.4 广义分叉引理

2006年，BELLARE和NEVEN[5]提出了分析数字签名安全性的重要工具:

引理2[5](广义分叉引理)假设q>1，集合H至少含有2个元素. 算法是一个随机算法，输入(x,h1,h2,…,hq)，可得输出(J,δ)，其中0≤J≤q. IG是一个随机算法,称为输入发生器. 算法的接受率acc为以下实验中J≥1的概率：随机选取和(x,h1,h2,…,hq). 基于算法的分叉算法GF同样为随机算法，其输入为x，具体执行过程如下：

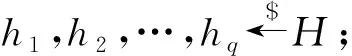
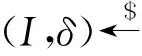
如果I=I′且hI≠h′I,则返回(1,δ,δ′)，否则返回(0,ε,ε).

2 TLMS方案

2018年，BAUM等[14]提出了一个基于格的高效同态承诺方案:

(1)KeyGen算法：构造矩阵A1和A2满足A1=[InA′1]，其中In为n阶单位矩阵，且且并输出矩阵A1、A2.

(2)Commit算法：为了承诺x随机抽取多项式向量计算承诺值并输出.

结合格上高效同态承诺方案，本文给出了TLMS方案，该方案包括MKeyGen算法、MSign协议和MVerify算法，各算法的执行过程如下：

(i)第1轮交互.

公布阶段：若签名者i为树结构Τ的根节点，则向子节点发送唯一的会话标识符ssid及消息m；否则等待接收ssid、m并将其发送至子节点.

承诺阶段：签名者i等待接收其子节点jCi发送的数据(tj,1,tj,2,apkj). 签名者i查询(b,e,f)←H0(m)，分别抽取和并计算承诺值和承诺值签名者i查询ui=H1(PK,pki)并计算部分聚合公钥若签名者i不是树结构Τ的根节点，则向其父节点发送数据(ti,1,ti,2,apki)，否则进入下一阶段.

(ii)第2轮交互.

挑战阶段：若签名者i为树结构Τ的根节点，则设置t1=ti,1、t2=ti,2以及apk=apki，查询c←H2(t1,t2,apk,m)，并向其子节点发送数据(t1,t2,apk). 否则，等待接收数据(t1,t2,apk)，查询c←H2(t1,t2,apk,m)，并向其子节点发送数据(t1,t2,apk).

响应阶段：签名者i等待接收其子节点jCi发送的数据(zj,gj). 签名者i计算z′i←αi+c·ui·ski. 若z′id-1 024×d-1 024，则设置并向其父节点发送数据(zi,gi)；否则重启签名协议. 若签名者i为树结构Τ的根节点，则设置z←zi和g←gi，并输出签名σ←(t1,t2,z,g).

(3)MVerify算法：给定一组签名者的聚合公钥apk、消息m和待验证多重签名σ=(t1,t2,z,g)，验证者查询(b,e,f)←H0(m)和c←H2(t1,t2,apk,m). 若z且则判定签名有效并返回1，否则返回0.

3 方案分析

3.1 正确性分析

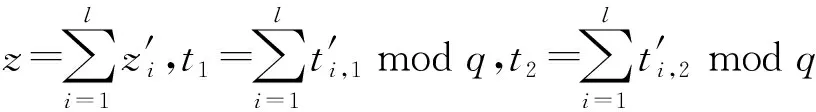
t1modq，

由此可知，TLMS方案是正确的.

3.2 安全性分析

定理1在随机预言机模型下，若存在1个概率多项式时间的伪造者，在至多进行qH次随机预言机查询、qS次签名查询且至多涉及lmax个公钥的前提下，成功伪造TLMS多重签名σ=(t1,t2,z,g)的概率为δ，其中承诺值t1,t2q，聚合后的签名l·(d-1 024)×l·(d-1 024)(l为签名者人数，部分签名d-1 024×d-1 024，d>1 024)，随机向量g则存在1个同样时间复杂度的算法，给定能够找到2个非零向量o1,o2q，使得a·o1+o2=0且的概率至少为其中，qA=δ-2(qH+lmax·qS)2/qn，DH1、DH2分别表示哈希函数H1、H2的值域.

证明假设参数x=(q,A,d)，其中Α=(a1)，多项式a服从q中的均匀分布. 给定攻击TLMS方案的伪造者，可构造1个模拟真实签名环境的算法，具体构造如下：

(1)输入：参数x，哈希函数H1的响应1,1,1,2,…,1,qH，哈希函数H2的响应2,1,2,2,…,2,qH，随机抛币ρ.

(i)随机预言机H0(m)查询. 算法查询表L0(m)，若其已定义则直接返回(b,e,f). 否则，算法从q中随机抽取多项式并存储于表L0(m)，随后返回L0(m).

(ii)随机预言机H1(PK,pki)查询. 算法查询表L1(PK,pki)，若其已定义则直接返回L1(PK,pki). 否则，算法查询表L3(pki)，若其未定义，则将公钥pki存储于表L3. 然后，算法解析公钥集合PK={pk1,pk2,…,pkl},并检查每个公钥pkjPK是否已存储于表L3. 在保证每个公钥pkjPK均存储于表L3后，再依据以下3种情况一次性赋值H1(PK,pkj)满足1≤j≤l：

①pkj=pk*且pk*PK；

②pkj≠pk*且pk*PK；

③pk*PK.

(iii)随机预言机H2(t1,t2,apk,m)查询. 算法首先查询表L2(t1,t2,apk,m),若其已定义则直接返回L2(t1,t2,apk,m). 否则，算法进行内部查询H0(m)并存储相关数据. 然后，算法增加计数器ctr2并设置L2(t1,t2,apk,m)=2,ctr2，返回L2(t1,t2,apk,m).

δ-2(qH+lmax·qS)2/qn.

(1)

(2)

(3)

A(z-z*)+(c*-c)apk=0,

(4)

输入参数x，运行分叉算法GF，得到其中，I=I′. 在分叉算法GF执行过程中，分叉点位于第I次随机预言机查询H1(PK,pk*). 在分叉点之前，算法模拟的2次执行环境是相同的，因此可知2次随机预言机查询H1(PK,pk*)的参数相同，即PK=PK′，pk*=pk*′. 此外，根据算法对随机预言机H1(PK,pkj)的响应可知：当pkj≠pk*时，当pkj=pk*时，从而可得apk≠apk′. 依据分叉算法GF的输出，可得2个聚合公钥等式:及假设公钥集合中包含l*个pk*，结合式(4)可得:

(5)

(6)

由式(5)、(6)，可得

A[(z-z*)(c*′-c′)-(z*-z*′)(c*-c)+

(7)

‖(z-z*)(c*′-c′)-(z*-z*′)(c*-c)+

256l·(d-1 024)+|l*|·643.

接下来需要证明

(z-z*)(c*′-c′)-(z*-z*′)(c*-c)+

(8)

依据文献[19]的思路，可在证明过程中选择系数稍大的多项式sk′(存在另一个多项式sk″，满足A·sk′=A·sk″). 若

(z-z*)(c*′-c′)-(z*-z*′)(c*-c)+

(9)

则存在另一个sk″，使得

(z-z*)(c*′-c′)-(z*-z*′)(c*-c)+

(10)

3.3 参数分析

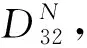
在实际选择TLMS方案参数时，综合考虑签名协议重复次数、多重签名长度和安全强度等因素，给出2组方案性能较优的参数集(表1).

表1 方案参数集Table 1 The sets of scheme parameters

以表1中参数集合I为例，介绍如何计算签名私钥长度、验证公钥长度、多重签名长度以及根式埃尔米特因子ξ. 签名私钥ski由2个从1中随机抽取的多项式si和vi组成，因此，签名私钥长度可表示为比特. 验证公钥pkiq,则验证公钥长度为比特. 多重签名σ由4个多项式组成，其中,t1,t2q，zl·(d-1 024)×l·(d-1 024),g因此，多重签名长度为比特. 此时，可得到TLMS方案的根式埃尔米特因子同理可知:TLMS方案选取表1中参数集合II时，私钥长度、公钥长度及多重签名长度分别为3 246、32 768、215 698比特，根式埃尔米特因子为1.005 5.

由表1可知TLMS方案所需参数较大，从而产生较长的公钥和签名. 但TLMS方案可支持公钥聚合功能，降低签名验证代价；且通过结合同态承诺方案减少签名者之间的通信次数，降低签名消耗的通信代价. 因此，TLMS方案是降低多重签名通信研究的一次有意义的尝试.

4 结论

多重签名是一种特殊的数字签名，其允许一组签名者合作对消息产生压缩的签名，可应用于合同签署、可信路由以及区块链等场景. 本文构造了一个基于格上困难问题并支持公钥聚合功能的两轮多重签名方案，在随机预言机模型中证明了该方案的安全性. 本方案具有较低的通信量和计算量，并能够抵抗量子攻击，可满足未来量子时代最新的安全需求.

然而，在随机预言机模型下证明安全的方案在现实应用中可能难以保证安全性. 因此，如何在标准模型下构造可抵抗量子攻击的有效多重签名方案可作为进一步的研究方向.