任 丹

（上海交通大学 安泰经济管理学院，上海 200030）

现代组合投资理论是建立在1952年马科维茨提出的均值-方差模型的基础之上。马科维茨运用方差和预期收益率对风险和收益刻画，企图在风险和收益之间寻求平衡，在这个过程中，收益率的协方差矩阵起到了分配风险和收益的桥梁作用。随着现代金融市场的发展，金融数据的维度变得十分庞大，通过历史数据估计得出的协方差矩阵往往呈现出奇异的特征，因此高维度情况下的协方差矩阵估计成了热门研究问题。

在传统研究和应用中，人们通常采用样本协方差矩阵作为总体协方差矩阵的估计量，但当矩阵的维度变得很大时，估计显得十分困难。尤其是横截面维度超过时间维度时，样本协方差矩阵是奇异的，均值方差模型是不能求解的。同时，估计过程中产生的累积误差会对最终的估计结果产生影响。为了解决前述问题，学者们提出了许多有效的估计方法，在金融投资实践中取得了显著的成果。

1 文献综述

高维协方差矩阵估计方法的研究主要集中在以下三个方面：1．基于因子模型的高维协方差矩阵估计，即通过有限的因子来达到降维的目的，得到有效的估计量，该方法在学界和业界均取得了显著的效果。2．压缩估计方法，该方法尽可能地保证估计量的特征向量同真实协方差矩阵估计量的关系，通过最小化损失函数来控制估计量的特征值。3．基于椭圆分布的高维协方差矩阵估计方法，该方法假设金融数据服从椭圆分布，建立了一系列性质优良的估计量。

本文首先介绍基于因子模型的高维协方差矩阵估计的一般方法。假设n个因子为Fnt构成的因子列向量为Ft，bt为各个因子上的暴露程度向量，eit为资产的特征收益，则相应的资产配置模型为

单个资产模型（1）整合成多维资产模型便有

假设特质收益et与公共因子Ft不相关，对模型（2）两边取方差便有

在模型（3）中，å为资产的协方差矩阵，W为因子的协方差矩阵，Se为特质收益的协方差矩阵，通常假设该矩阵为稀疏的。从估计流程不难发现，有限的因子起到了降维的作用，同时保证了估计得出的协方差矩阵是非奇异的。基于因子模型的高维协方差矩阵估计方法主要分为两类：可观测因子和不可观测因子。二者的整体框架是一致的，不同点在于因子的刻画上。

从可观测因子的研究角度来看，学者认为资产收益率可以由公共因子解释，比如市场收益率、市值、估值等因子，通过这些公共因子达到降维目的。Sharpe（1964）最早提出了单因子模型，认为股票的收益率可以由市场收益率解释（CAPM）。Fama和French（1993）认为企业自身因素才是影响资产价格的重要因素，采用市值、账面市值比和市场收益率作为新的因子对资产定价。可观测因子的好处在于因子的易获得性和可解释性强。

从不可观测因子的研究角度来看，研究者提出的最典型方法为主成分估计法（PCA）和极大似然估计。主成分估计法是通过对样本协方差矩阵进行分析，获得相应的主成分作为主要的因子。典型地，如Fan（2013）提出了基于主成分的非参估计量——主成分正交补阈值估计量（POET）。但是主成分分析法主要是基于样本协方差矩阵来完成的，样本协方差矩阵的特征值和特征向量对与因子相关的假设检验起到了约束作用。为了突破此局限，Doz等（2012）将极大似然估计引入高维协方差矩阵估计领域，Bai和Li（2012，2016）完善了此框架，并证明了极大似然估计量的一致性。

压缩估计方法主要分为两类：线性压缩和非线性压缩。从线性压缩方法的研究角度来看，给定压缩目标和样本协方差矩阵，最小化二者的线性组合与真实协方差矩阵之间的距离，来获得最优的线性压缩权重。该方法不考虑具体的因子和因子结构，通过压缩目标对样本协方差矩阵进行改进。Ledoit和Wolf选取单指数模型等相关稀疏矩阵和单位阵作为压缩目标，利用美股数据做了实证研究，发现单位阵的表现效果是最好的。从非线性压缩的研究角度来看，该方法是控制样本协方差矩阵的特征向量不变，对特征值进行优化，Leodit和 Wolf（2012，2014a，2015）系统地研究如何将非线性压缩的不可解转化为依赖样本特征值极限分布的理想估计量，再利用前面得出的估计量进行优化分析。

通常的金融研究中，研究者们会假设收益率向量服从高维正态分布，即X∶Nd（m，S），但是金融市场中的数据大多呈现出非正态和厚尾的特征，因此学者们通常假设金融数据服从椭球分布，以此为基础提出新的高维协方差矩阵估计方法。协方差矩阵可以分解成皮尔逊相关系数矩阵和资产标准差对角阵的乘积，即

问题转化为对皮尔逊相关系数矩阵和标准差对角阵D的估计，Zhao和Liu（2014）基于这一思路提出了EPIC估计方法。对于皮尔逊相关系数矩阵R的估计，Fan等（1990）提出了正弦变化的肯德尔t估计量，即计算资产i和资产j之间的肯德尔t相关系数，并用正弦函数进行转换后作为矩阵R的（i，j）元估计。Catoni（2012）提出了均值和标准差的M—估计量，该估计量在厚尾分布中表现出极好的性质，可以作为标准差对角阵D对角元的估计量。沿着这一方向，许多学者提出了新的估计方法，如Liu等（2014）提出的EC2估计法。

由于国内的金融市场发展较国外晚，国内学者对高维协方差矩阵估计的研究是最近几年才兴起的。刘丽萍（2016）将主成分法和门限方法相结合，提出了门限主成分正交补（TPO）估计量，并通过实证发现该方法能提高协方差的估计效率、有效降低噪声的影响。赵钊（2017）总结了国内外学者对高维协方差矩阵估计问题的相关文献，发现非线性压缩方法提高了DKK和BEKK模型的估计效率，在高维协方差矩阵估计方面起到的重要作用。宋鹏、胡永宏（2017）提出了基于Cholesky分解的可预测值因子模型，并同VAR-LASSO方法进行比较，发现其在降维方面的优势较为明显且二者的估计误差接近。

目前国内外学者对高维协方差矩阵的研究已经十分深入，对后续的研究具有重要的借鉴意义。本文的研究是基于Ledoit和wolf的线性压缩模型，将压缩目标改为协方差矩阵的另一个估计量，即将距离多个估计量线性组合最近的对称正定矩阵作为高维协方差矩阵的估计量。本文的创新之处在于克服了Ledoit和Wolf中的线性压缩估计模型之中必须有一个正定矩阵的限制，并考虑了估计量的稀疏性问题，同时对该方法在资产配置中的实际运用进行了实证研究。

2 模型

Ledoit和Wolf（2003）认为给定样本协方差阵S和压缩目标矩阵F，最优的估计量应该是二者的线性组合。定义二次损失函数（总体协方差阵）如下：

最小化二次损失函数（5）便可以得到最优权重a*，但总体协方差矩阵S是未知的，因此Ledoit和Wolf（2003）从统计角度给出了最优权重a*的估计量a*est，故样本协方差矩阵的最优估计量可以写成样本协方差矩阵和压缩目标矩阵的线性组合：

Ledoit和Wolf（2003）认为样本协方差矩阵S和压缩目标矩阵F中至少有一个矩阵是正定可逆的，这样可以保证最后的估计量W是可逆的。但当压缩目标矩阵和样本协方差矩阵均不正定时，最后的估计量便不具备正定性的特征。

假设Sn＋为对称正定矩阵的集合，借鉴压缩估计量的思想，假设F和S均为协方差矩阵的估计量，本文想求解距离该凸组合距离最近的对称正定矩阵作为总体协方差矩阵的估计量，即求解以下优化模型（7），来确定最优的样本协方差矩阵估计量X*：

当a给定的时候，模型（7）转化为最近相关矩阵问题（nearest correlation matrix）。最近相关矩阵问题如下：给定矩阵GÎSn＋，求解距离其最近的对称正定矩阵：

模型（8）已经被很多学者进行了研究。Qi和Sun（2006）提出了高斯梯度下降法来求解模型（8），并取得了显著的效果。学者们不满足于模型（8）的求解，因为最佳的协方差矩阵估计量具有一定的稀疏性。因此，在问题（8）的基础上，Liu等（2014）提出了在目标函数中引入惩罚项来保证解的稀疏性，即

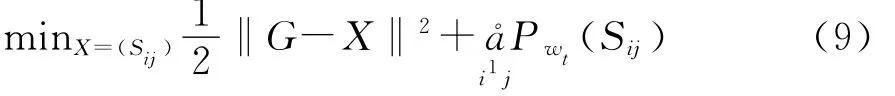
其中，Pwt（x）为惩罚函数，起到控制优化结果稀疏的作用。因此，本文在模型（7）的目标函数中加入l1惩罚函数，使得模型的优化结果具有稀疏性，即

接下来，本文会讨论模型（7）和模型（10）的求解方法。

3 模型求解方法

定义无偏估计量G1和G2的凸组合为

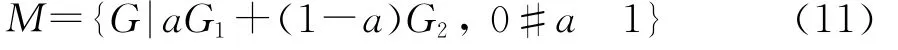
在模型（7）的基础上，加入条件X3eI，目的是控制优化结果特征根的范围，因为金融资产始终是存在波动的e，在这里假设最小波动为e。因此，模型（7）便更新为

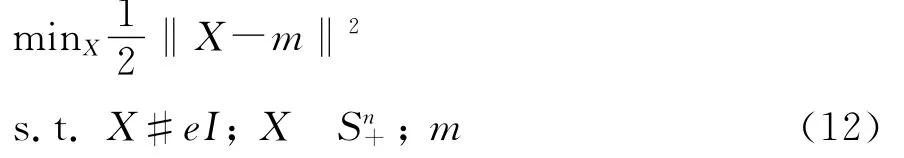
对于模型（12）给定m0，假设m0的n个特征值为l1（m0），…，ln（m0），则m0的谱分解为m0＝åni＝1li（m0）vivi，那么模型（12）的最优解为X*＝åi＝1max（li（m0），e）vivi′。由于模型（12）的目标函数本身是凸函数，当给定m0的时候，模型（12）存在前述解析解，为了确定最优的a，采用三分法进行求解。模型（12）的目标函数为l（a，X）＝1／2‖X-aG1-（1-a）G1‖2，不断迭代a，使目标函数的差值直至收敛，具体的迭代算法如下：

模型（12）的迭代解法：

1．初始化：a0＝0，a1＝1／3，a2＝2／3，a3＝1，阈值d；

2．计算相应的目标函数值：l（a1，），l（a2，）；

3．如果l（a1，）＞l（a2，）：

a0＝a1，a3＝a3，a1＝a0＋1／3（a3-a0），a2＝a0＋2／3（a3-a0）；

如果l（a1，），l（a2，）：

a0＝a0，a3＝a2，a1＝a0＋1／3（a3-a0），a2＝a0＋2／3（a3-a0）；

4．循环上述步骤到两次结果的绝对值小于d时，停止迭代。

在模型（12）中，考虑的是求解距离给定凸组合最近的对称正定矩阵，但是在实际运用中，优化结果的稀疏性也是必须考虑的重点之一，所以加入l1惩罚方程，便有

给定m0，模型（13）转化为

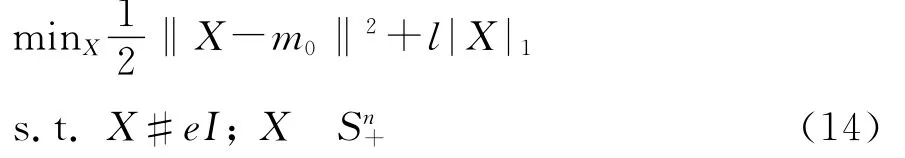
当m0给定的时候，问题就转变为Xue（2012）研究的问题，其求解方法主要是可选方向迭代算法（alternating direction method），Xue（2012）引入新的变量，将模型（14）改写成如下形式，即

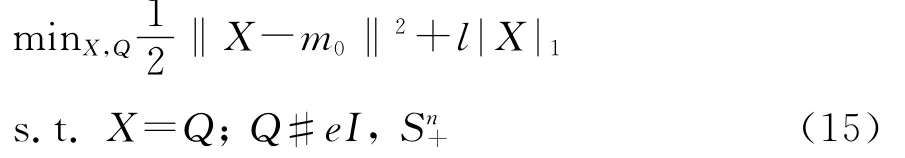
Xue为了求解该问题，采用矩阵形式的拉格朗日方法，即写出模型（15）的拉格朗日方程，便有

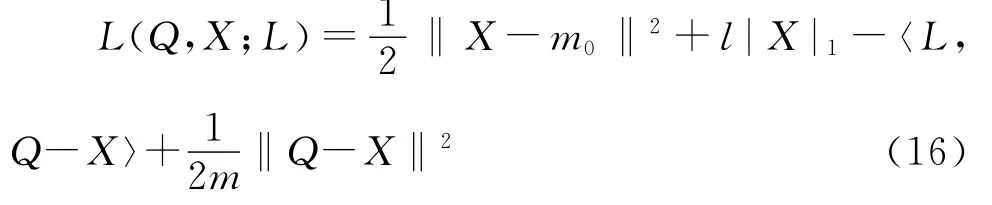
对于模型（16），Xue建立了可选方向迭代算法（alternating direction method），并证明了该算法能收敛到最优的解以及解具有良好的统计性质，求解的算法步骤如下：

模型（16）的迭代解法：

1．初始化：m，X0，L0；

2．第步迭代过程如下：

（1）求解Qi＝（Xi＝m Li）＋；

（2）求解Xi＋1＝｛S（m（m0-Li）＋Qi＋1，lm｝／（1＋m）；

（3）求解Li＋1＝Li-（Qi＋1-Xi＋1）／m；

3．循环上述步骤至收敛。

上述S为阈值函数，对矩阵的非对角元进行控制，在给定矩阵G时，具体形式如下：

对于模型（14），结合上面可选方向理论算法以及f（a，X）是［0，1］′Sn＋上的凸函数，运用三分法求解相应的结果，具体算法步骤如下：

模型（13）的迭代算法：

1．初始化：a0＝0，a1＝1／3，a2＝1及阈值d；

2．运用可选方向理论算法求解：f（a1，X*1），f（a2，X*2）；

4．循环上面的步骤到两次结果的绝对值小于d时，停止迭代。

附录里给出算法（13）的收敛性证明，但是模型（13）的求解方法属于暴力求解算法，模型求解速度慢。因此，本文对于模型（13）只做理论上的探索，不考虑进行实证分析。

4 实证

本文实证数据来自已有的A股数据，时间跨度为2014年1月1日至2017年12月31日，剔除节假日，实际交易日共977天。本文采用最小方差模型来衡量估计出的协方差矩阵的优劣。最小方差模型是指通过最小化风险获得投资组合中的资产权重，然后根据求出的权重进行组合投资。求解带惩罚项的协方差估计模型具有极大的计算成本，因此本文的实证部分不进行探讨，故只考虑不带惩罚项的协方差矩阵估计模型。

假设估计样本协方差矩阵的时间窗口长度为T，利用2T的数据估计出两个协方差矩阵，再用不带惩罚项的模型求得相应的协方差矩阵估计S。为了检验协方差矩阵估计的优劣，本文采用的模型为最小方差模型，通过最小化波动率来获得全市场股票的投资权重，模型为

其中，q为资产组合中资产的权重，S为通过前述算法得到的协方差矩阵。根据模型（18）所求权重构建投资组合，并考虑该投资组合在未来一年里的收益曲线，计算相应的年化收益率Rt、方差st、夏普比率ST t。将时间由t变成t＋1，重复前面的步骤，获得年化收益率Rt＋1、方差st＋1和夏普比率SRt＋1，这样便可以得到年化收益率序列、方差序列和夏普比率序列。

取窗口长度T为100、200、300天，得到上述不同序列，计算相应指标的均值得到表1结果。

从年化收益的角度来看，不同周期下的估计模型对应的年化收益率均值均高于基准指数的年化收益均值，二者比值的变动区间为［3．13，3．23］；从波动率的角度来看，二者波动率比值的变动区间为［0．95，1．17］；从夏普比率的角度来看，二者夏普比率比值的变动区间为［2．48，2．93］。以上三个指标的比较表明，基于估计模型的资产组合表现比基准组合更加优异，能够获得超额收益，本文的基准组合为上证综指。

表1 不同周期下的评价指标结果

表1结果是从均值角度出发来进行比较的，不能充分反映每个指标在时间维度上的变化情况，因此本文绘制了不同指标随着时间变化的曲线，得到的结果如图1、图2、图3所示。

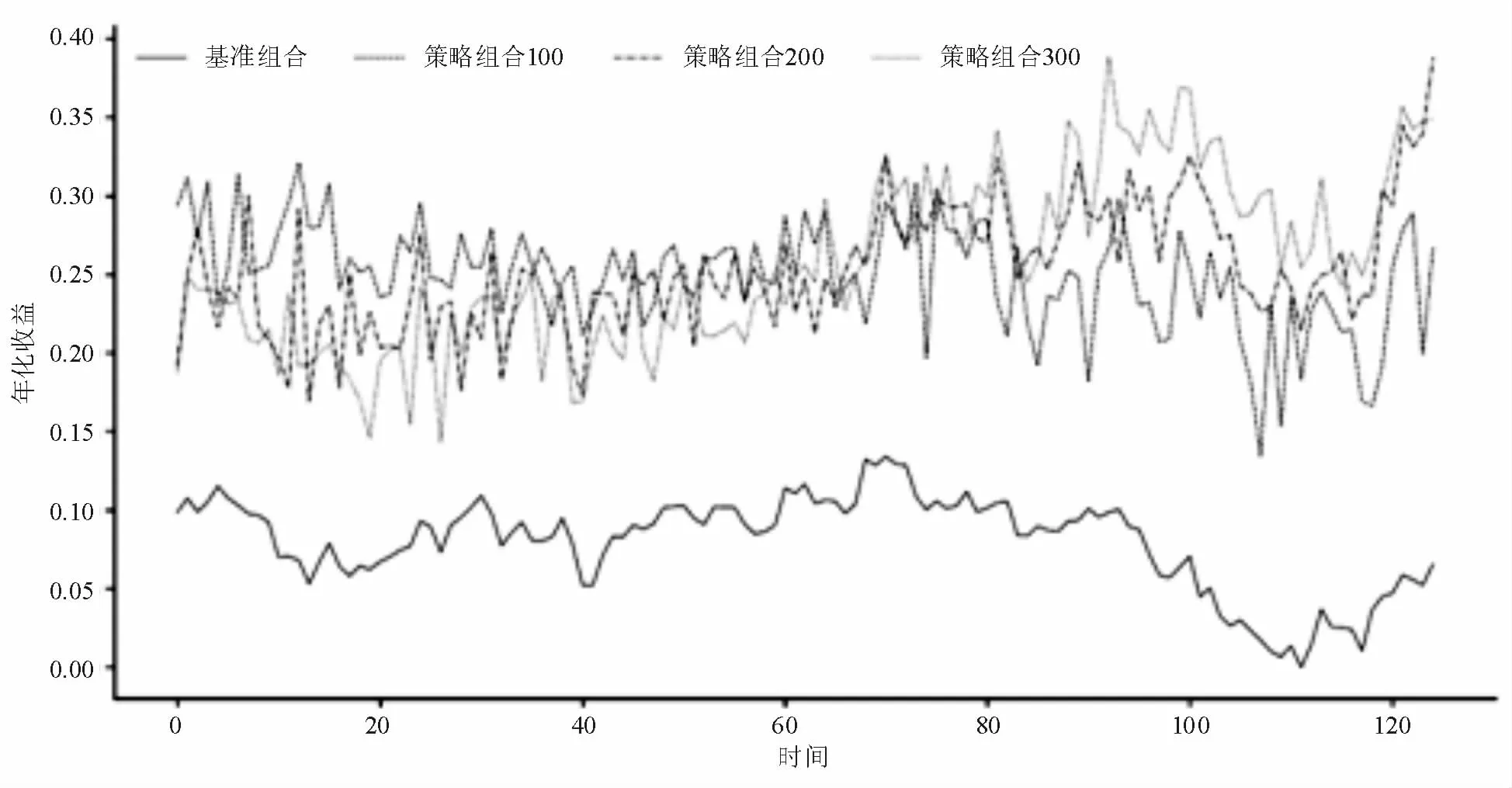
图1 不同组合年化收益率变化曲线

图2 不同组合波动率变化曲线

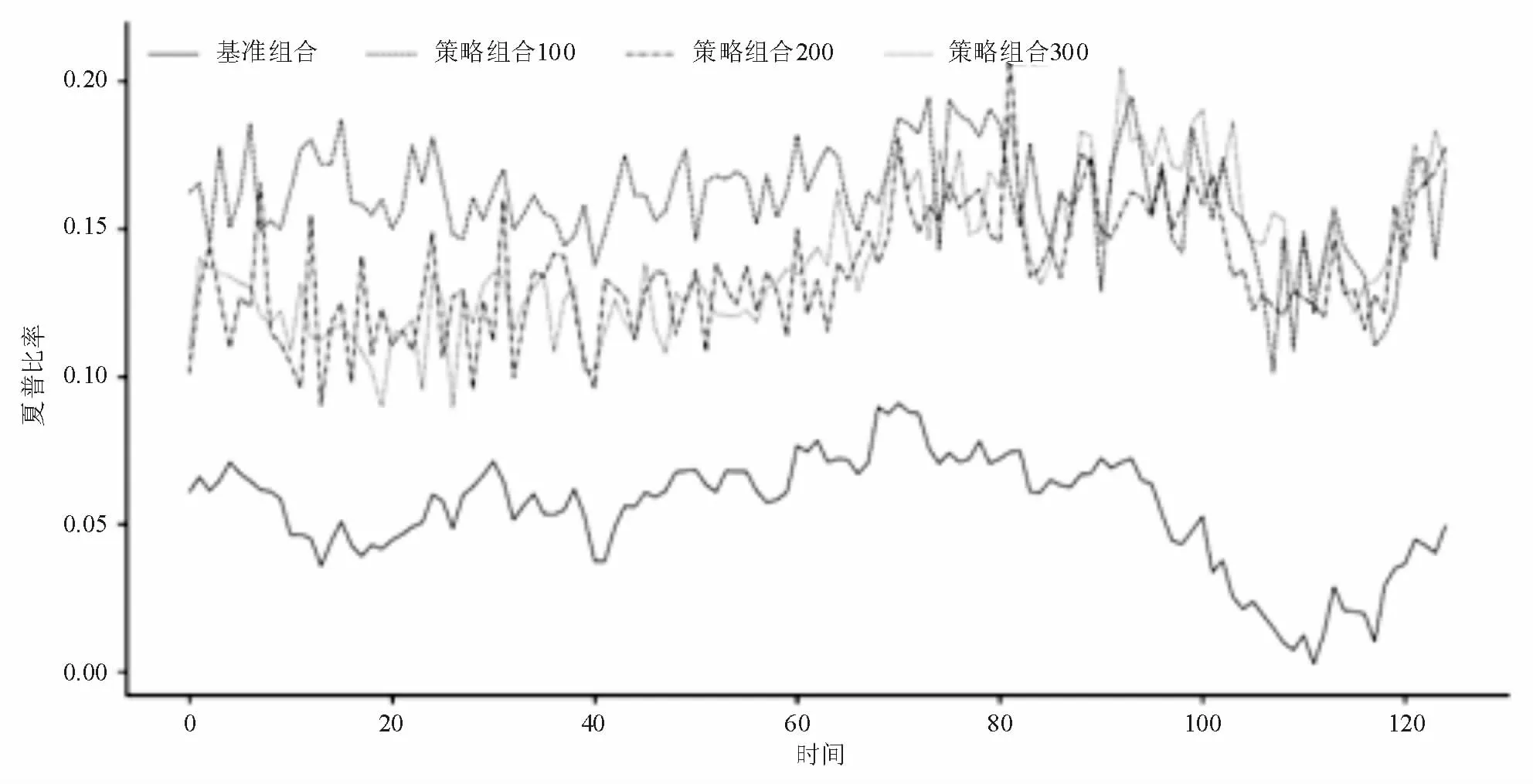
图3 不同组合夏普比率变化曲线

图1 的年化收益率曲线表明估计模型的年化收益率是高于基准的年化收益，图2的波动率曲线表明估计模型的风险暴露程度在绝大多数情况下是高于基准的，图3的夏普比率曲线表明估计模型所获得夏普比率是高于基准的夏普比率。总而言之，基于估计模型的资产组合与基准资产组合相比较，其在承担更多风险的同时，获得了更高的资产收益，且对风险分散十分有效，单位风险所获得的收益更高。

5 结论

随着金融市场的发展，金融产品的种类越来越多，金融数据呈现出爆炸级的增长态势，这给传统的资产配置模型带来了新的挑战——资产维度超过时间维度导致样本协方差矩阵奇异问题，因此如何有效地估计高维协方差矩阵引起了研究者们的极大兴趣。本文回顾了高维协方差矩阵估计领域的研究成果，对不同的研究思路进行了总结。

本文的研究主要是在Leodit和 Wolf（2003）的压缩估计量的研究成果基础上展开的，从运筹优化的角度出发，提出了新的估计方法，即寻找距离多个无偏估计量的凸组合最近的对称正定矩阵作为高维协方差矩阵的估计量。按照对优化结果稀疏性的要求，本文讨论了两种估计模型：1．不带惩罚项的模型；2．带惩罚项的模型。对于上述两种模型，本文给出相应的解法和解法的收敛证明。在理论部分之后，本文结合A股的数据对不带惩罚项的模型方法进行了实证研究，即基于不带惩罚项模型求出协方差矩阵的估计量，采用最小方差模型构建投资组合，获得相应的年化收益率序列、波动率序列和夏普比率序列。通过与基准组合的比较发现，该方法相对于基准带来了显著的超额收益，取得了较好的投资效果。