XU Xiao(徐 晓), ZHOU Wei(周 伟)*, CHU Tong(褚 童)

1 College of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, China 2 College of Law, Zhejiang University of Finance and Economics, Hangzhou 310018, China

Abstract: The symmetric dynamical model of a Cournot duopoly based on conjectural variation is established. Local stability of the equilibrium point is analyzed and the invariant sets are given. Then, dynamic behavior is studied by numerical simulation. With the change of gradient adjustment parameters, the routes to chaos vary. Synchronization occurs along the invariant sets accompanied by the on-off intermittency through the analysis of transverse stability. Coexistence of multiple attractors and structure of basins of attraction being more complex indicate more complicated bifurcation phenomena.

Key words:conjectural variation; synchronization; transverse stability; Milnor attractor; coexistence of attractors

Introduction

In the study of the oligopoly market, Cournot first proposed a duopoly model with outputs as competition. Bertrand proposed an oligopoly model with prices as competition. Bowley put forward an oligopoly model based on conjectural variation. In 1978, Rand[1]studied the dynamic oligopoly game firstly, which was a great breakthrough for the research on oligopoly. In order to be more pragmatic competition in the market, the Cournot model has been improved by a large number of scholars. It has been found that with the duopoly competition, bifurcation and chaos occur in the system. In the field of nonlinear oligarchs, global dynamics analyses, synchronization phenomena and the coexistence of multiple attractors are included, which have attracted many scholars. Bischi and Kopel[2]studied multistability in a dynamic competition model. Askaretal.[3]researched the chaotic phenomena in dynamic Cournot duopoly games. Fantietal.[4]discussed the occurrence of synchronization in the Bertrand’s duopoly model. Researchers[5-6]discussed the complex dynamics with bounded rationality. Zhouetal.[7]studied a two-stage Cournot game with R & D spillover and product differentiation. Lardon[8]researched the cooperative Bertrand and Cournot oligopoly games with transferable utility on the basis of their non-cooperative foundation. Shi and Xu[9]researched a dynamic quantum Cournot duopoly game with heterogeneous players. It was a leap from the static game to the dynamical oligopoly based on the nonlinear theory. However, there are also some problems. In the complex dynamic model of the oligarch game, the analysis of dynamic behavior by combining conjectural variation with quadratic cost function is few. In the references of oligarch games, most of them discuss the chaotic phenomena of systems, but the numerical simulation is relatively simple. Researches on the coexistence of attractors and synchronization between firms are few. Firstly, based on above problems, we introduce the conjectural variation, and establish a dynamic model of duopoly with nonlinear cost function based on conjectural variation. In the market, firms have limited information about competitors, but they know the marginal profit function of constant conjectural variation. Firms adjust outputs by considering the competitors in addition to themselves. The path dependence is studied by the bifurcation diagrams. Secondly, although the initial value conditions of two firms are different, the synchronous behavior occurs in the long term with the change of parameters. The transverse stability restricted on the invariant sets is studied by characterizing the transform Lyapunov exponent. When the system is transverse stable, it often accompanies the occurrence of synchronization. And at the same time, points on the diagonal attract the attractors off the diagonal, so the coexistence of attractors occurs. In addition, the system is accompanied by intermittent phenomena. Finally, the global bifurcation of the system is studied by characterizing the critical curves[10]. By changing the parameters, we study the coexistence of attractors and the change of the basin structure.

The paper is organized as follows. In section 1, the symmetric Cournot duopoly model based on the conjectural variation is established, and the invariant sets are given. In section 2, the fixed points and their local stability are studied. In section 3, due to the symmetric of the model, it is inferred that synchronization happens in the long run accompanied by the intermittency. So the invariant sets are studied. And the periodic and chaotic behaviors are studied by using the bifurcation diagrams, the transverse Lyapunov exponent and time series diagrams. Besides, the critical curves and the evolution of attractors and basins of attraction are studied by numerical simulation, which shows the complicated dynamical behaviors through the change of parameters. Section 4 represents the conclusions.

1 Models and Invariant Sets

Assuming that the utility function is quadratic, there is a linear and classical inverse demand function[11]. Therefore, the utility function can be defined as

wherea>0, andb>0.adenotes the maximum price,brepresents the measurement of the decrease in price when per quantity of product increases, andqis the quantity of the product purchased by the consumer.

Provided that the market price is denoted byp, in order to gain sufficiently large profits, the consumer solves the optimization problem, which is

max{U(q)-pq}

Firms adjust outputs to achieve internal optimization constantly, so the first order condition indicates that

[U(q)-pq]′=U′(q)-p=0,p=a-bq.

(1)

It is discovered that the linear condition between the quantity and the price of the product is satisfied. Supposed that there are two firms in the market, both of them are cooperative or competitive. Therefore,

where

The form of cost function considers not only the output adjustment of the firms, but also the impact of competitors. So the cost function can be complicated when taken the market environment and inside factors into account. The cost will be affected by technology, work force and material resources in the market so that the cost function is nonlinear and more complex. In this way, there is a point in defining cost function as quadratic,

Ci(q1,q2)=ciqi+eiqi2.

wherecidenotes the cost coefficient corresponding to per product when a single factor is considered, andeiis the cost coefficient which is relevant to the nonlinear cost function.adenotes the maximum price， soa>c.

Therefore, the profit function of the firmiis denoted by

(2)

Firms adopt adjustment mechanism to update production decisions, which plays a significant role in the local stability analysis of the equilibrium and global dynamics. Considering a discrete time adjustment process that is similar to the gradient process based on marginal profits, we suppose that the change about quantities is proportional to the marginal profits,

(3)

whereηi>0.

Two firms have discrete time dynamic equations as

(4)

Due to the dynamic change of the market, it is impossible for firms to be independent. Therefore, the output of firms is affected reciprocally. It is necessary to introduce the constant conjectural variation, dqj/dqi=γi, andγiis variation of the firmi. Firms have limited information about the adjustment of production, which is predictable to some extent. Therefore, Eq. (4) can be further denoted as

(5)

The analysis is restricted to the circumstances,a1=a2=a,b1=b2=b,c1=c2=c,e1=e2=e,η1=η2=η, andγ1=γ2=γ.

The map about two dimensional nonlinear dynamics can be denoted by

(6)

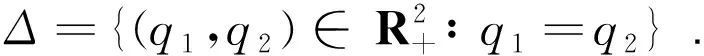
2 Fixed Points and Stability Analysis

Firstly, the fixed points of dynamic system (6) are the solutions of quadratic equations

(7)

Proposition 1 Equation (7) has four fixed points for all parameters,

It is evident that the outputE3of two firms is identical, which is denoted asE3=(q0,q0).E0is origin, andE1andE2are located on coordinates which are boundary points.E3is the internal fixed point, which is called Nash equilibrium[12-13].

In the following, the local stability of the fixed points is determined by the eigenvalues. The Jacobian matrix of Eq. (6) is

The eigenvalues ofJare denoted byλ‖andλ⊥.

Theorem 1 The equilibrium is local stable, if and only if the modulus of the eigenvaluesλ‖andλ⊥are less than 1.

Theorem 2E0is an unstable node.

Theorem 3E1andE2are unstable.

with the form of a triangular matrix, the eigenvalues are

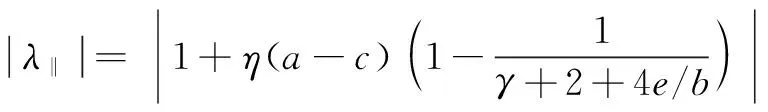
Theorem 4 The Nash equilibriumE3is local asymptotic stable if it is satisfied

Proof

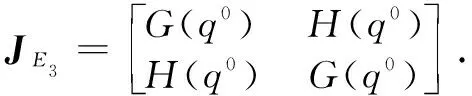
λ‖=G(q0)+H(q0),λ⊥=G(q0)-H(q0).

The eigenvalues are

|λ‖|=|1-η(a-c)|，

E3is local asymptotic stable, if and only if the modulus ofλ‖andλ⊥are less than 1.

3 Dynamical Analysis

In the numerical simulation,q1=0.36,q2=0.40,a=1.04,b=0.28,c=0.40,e=0.42, andγ=0.32. To avoid the transient, thousands of iterations are carried out, and the last dozens of iterations are taken to simulate the bifurcation diagrams(shown in Fig. 1). In Fig. 1(a), with the increase ofη, the system changes from period-1 to period-2, and then to period-4. Figure 1(b) is the partial enlargement of Fig. 1(a). Combining with Fig. 1(b), the system leads to chaos from period-4 whenηreaches 3.90. With the further increase of parameters, the system changes from chaos to period-8, and then to chaos. The system presents period doubling bifurcation asηchanges, which is accompanied by chaos. In other words, the Nash equilibrium point loses its stability with the increase of parameters. Furthermore, the system is a stable state when corresponding to period-1. As the parameter increases, the phenomena are more complicated. The period doubling bifurcation and chaos occur, making picturesque dynamical behavior.

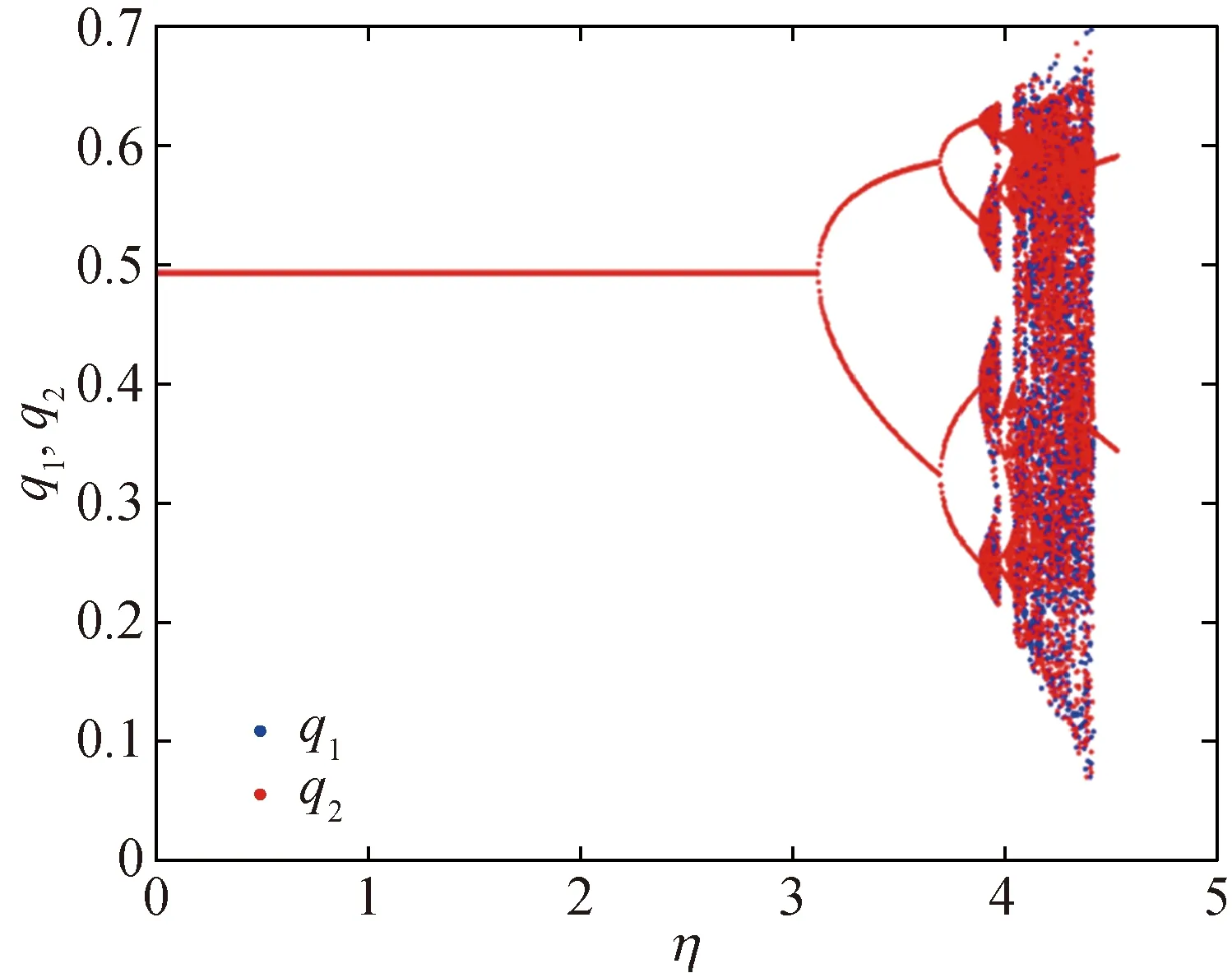
(a)

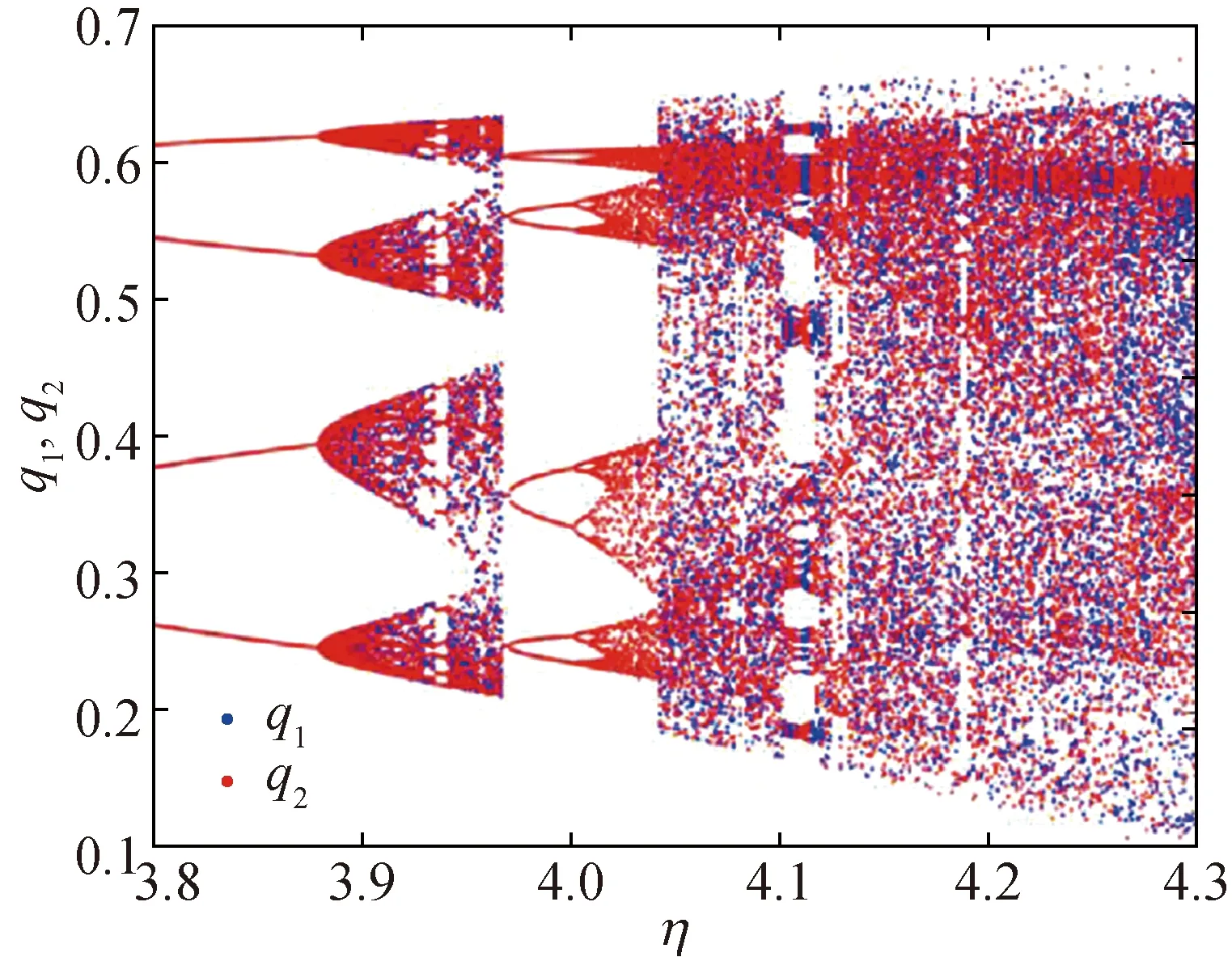
(b)Fig. 1 Bifurcation diagrams of η

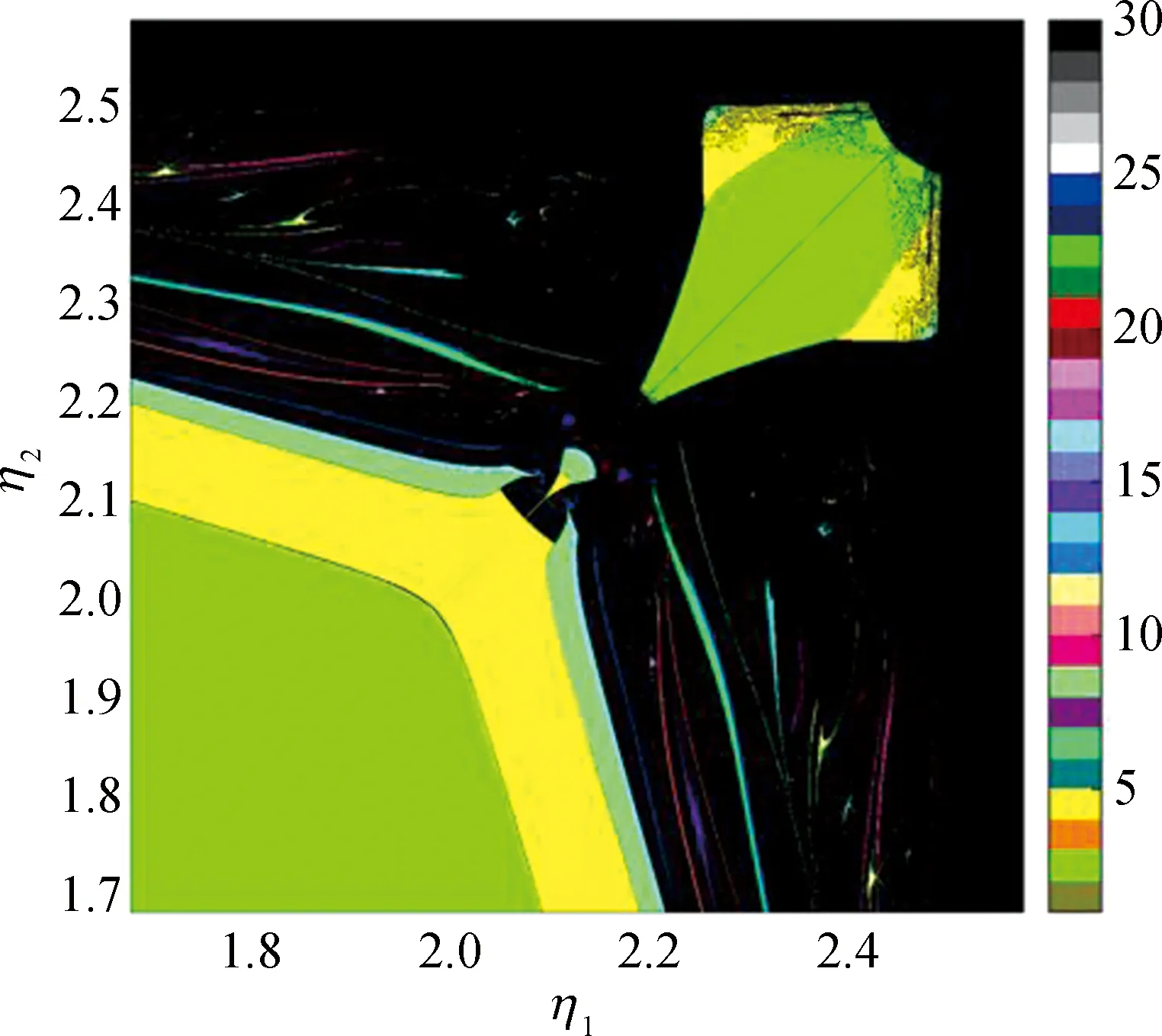
Asηchanges, the Nash equilibrium point loses its stability, and period doubling bifurcation and chaos occur. Now two-dimension parameter bifurcation diagrams are utilized to study the path to chaos, and the change of the stability region under different Nash equilibrium points. Figures 2(a)- (b) are obtained in specific parameter bifurcation diagrams. Different bifurcation routes are dependent not only on various bifurcation parameters, but also on the selection of the initial, the phenomenon of which is called path-dependence. Due to the difference of the parameters and the initial path, paths leading to chaos are multiple.

In Fig. 2(a),q1=0.10,q2=0.10,a=2.01,b=0.12,c=0.67,e=0.17, andγ=1.65. There is just one route leading to chaos on and off the diagonal. The system undergoes period doubling bifurcation and then leads to chaos by way of the flip bifurcation. In Fig. 2(b),q1=0.50,q2=0.50,a=1.30,b=1.60,c=0.10,e=0.20, andγ=1.00. Different from Fig. 2(a), two routes exist that lead to chaos. One is flip bifurcation that is from period doubling bifurcation to chaos along the diagonal. The other is off the diagonal, which is from period-1 to chaos directly. In this circumstance, the system undergoes Neimark-Sacker bifurcation[14].

(a4)

(b)Fig. 2 Two-dimension bifurcation diagrams of η1 and η2

In this subsection, we study the mechanisms that route to the synchronization in the long run. A trajectory, starting outΔwhich meansq1(0)≠q2(0), is said to synchronize if |q1(t)-q2(t)|→0 whent→+∞[15].

(a)

(b)

(c)

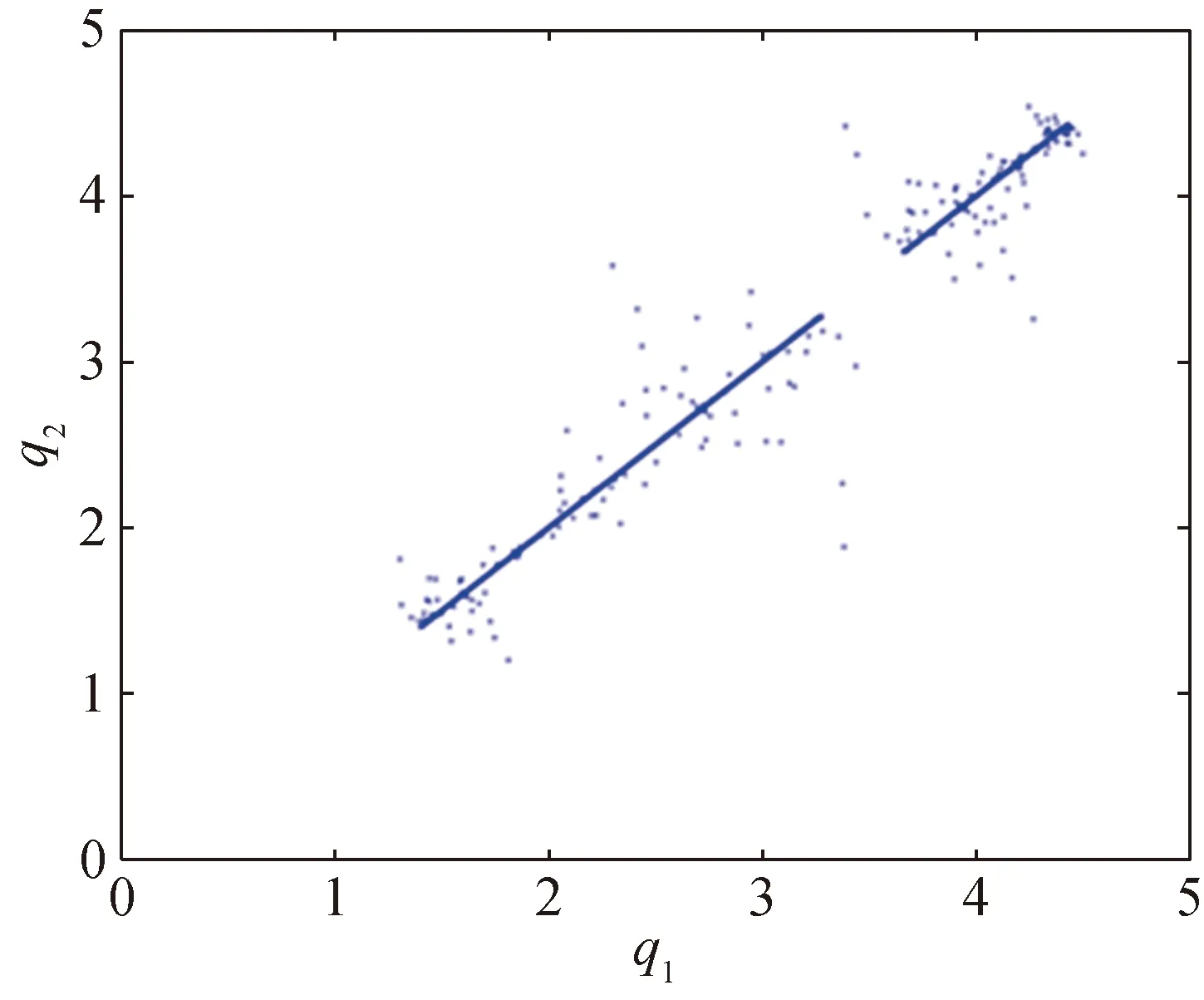
(d)

Fig. 3 Transverse stability and synchronization: (a) bifurcation diagram ofηranging from 1.918 to 2.200 for the restriction of the mapFtoΔ; (b) the transverse Lyapunov exponent ofηcorresponding with (a); (c) the trajectory bursts away from the diagonal before synchronization withη=1.970 versus time; (d) the transient of the trajectory starting from the initial condition as in (c) before converge toΔ

After studying the phenomenon of synchronization with the change ofη, the global dynamical behavior and contact bifurcation are introduced asb(measurement of the decrease of price when per quantity of product increases) changes next. Asbincreases, the quasi-periodic attractor on the diagonal loses the transverse stability. And the synchronization behavior disappears gradually. Therefore, firms will adjust the price properly in the market and gain profits as much as possible.

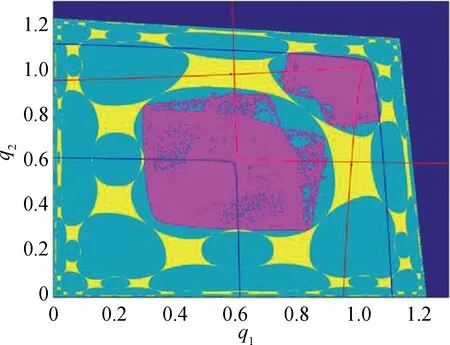
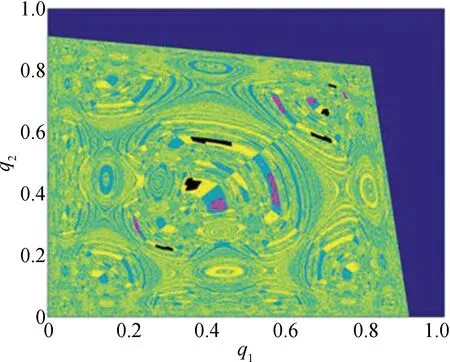
The dynamical behavior with the change ofbcan also be illustrated by Figs. 4(a)- (d).a=2.39,c=1.07,e=0.51,η=1.99, andγ=2.05. Color of black and magenta represent different attractors. In Fig. 4(a), the quasi-periodic attractor on the diagonal, which means Milnor attractor, and the period-2 attractor off theΔ, are coexisting. The initial condition off the diagonal converges to theΔin the long run, therefore synchronization occurs[17]. Asbincreases, the structure of the basin in Fig. 4(b) is similar to that in Fig. 4(a). In this case, boundary of the strange attractor on the diagonal contacts with the basin, and the critical line also contacts with the boundary of the attractor. At this time, the global bifurcation occurs. It is visual that attractor changes and finally disappears. The structure of basins of attraction has changed. Although two kinds of attractors coexist at this time, the weak attractors on the diagonal disappear, and two pieces of chaotic attractors are evolved, which is called chaotic. In Fig. 4(c), asbfurther increases, the structure of the basin changes, and the coexistence of attractors disappears, leaving six-piece strange attractors being symmetric about diagonal only. In Fig. 4(d), the structure of the basin changes and becomes more complicated asbincreases further. Two types of chaotic attractors coexist. The behavior is various, which is closely related to the production of the firms in the market. With the increase of production, the firms prefer to decreasebappropriately. The synchronization is related tobof small values. Two firms reach synchronous and dynamic balance states in the long run.

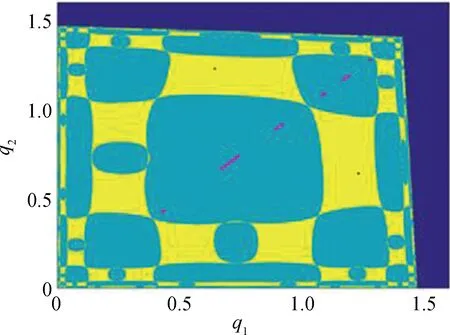
(a)

(b)

(c)

(d)

Fig. 4 Evolutions about the basins of attraction: (a)b=0.10, the coexistence of the Milnor attractor and the period-2 attractor with the basin of attraction; (b)b=0.23, two-piece strange attractors and the period-2 attractor with the basin of attraction and the critical curves of mapF; (c)b=0.41, six-piece strange attractors and the basin of attraction; (d)b=0.48, two symmetric strange attractors (six-piece) and the basin of attraction

4 Conclusions

The synchronous dynamic behavior of the system is studied. Our aims are to research the case in which two firms have an identical dynamical phenomenon, which means synchronous. It is found that different initial values route to different paths of the chaos. With the analysis of the transverse stability, the Milnor attractor and the attractors off the diagonal are coexistent. In the end, the condition that the attractors on the diagonal coexist with the attractors off the diagonal is obtained. Then, synchronization occurs. Firms prefer to adjust the values to achieve the balance dynamically in the market.