薛巧蕊 朱涵

摘要 以北京豐台站六线简支钢箱叠合拱桥为工程背景，利用MIDAS/Civil建立六线简支钢箱叠合拱桥的有限元模型，对成桥状态下的拱肋在不同工况下的受力情况进行分析，在三线偏载情况下拱肋竖向位移达到最大值129.3 mm，比六线全载情况下稍增加3.7 mm，拱肋最大压应力达到208 MPa，比六线全载情况下稍增加7 MPa，在三线偏载情况下对拱肋受力最不利，但拱肋位移及应力均满足规范要求，在使用阶段的安全性得以保证。分析了温度对拱肋位移的影响，拱肋各部位竖向位移变化呈抛物线形，随着拱肋与拱脚之间距离的增加，竖向位移值增大，在拱顶处达到最大值，拟合出了拱肋位移与温度之间的关系，为预测六线简支钢箱叠合拱桥的温度变形提供相关依据;同时分析了拱肋与主梁刚度比变化对拱顶在不同温度下的竖向位移进行了分析，提高拱肋刚度可以减小拱肋竖向位移。

关 键 词 钢箱叠合;拱肋;受力分析;温度;刚度比

中图分类号 U448.22     文献标志码 A

Mechanical analysis of arch rib of six-line simply supported steel box composite arch bridge

XUE Qiaorui1，2， ZHU Han1

（1. College of Architectural Engineering， Tianjin University， Tianjin 300072， China; 2. China Railway Sixth Group Tianjin Railway Construction Co Ltd， Tianjin 300232， China）

Abstract Based on the engineering background of Beijing Fengtai Station six-line simply supported steel box composite arch bridge， the finite element model of six-line simply supported steel box composite arch bridge is established by MIDAS/Civil. The stress of arch rib under different working conditions is analyzed. The maximum vertical displacement of arch rib is 129.3 mm under three-line eccentric load， which is 3.7 mm higher than that under six-line full load， and the maximum compressive stress of arch rib is 208 MPa， which is 7 MPa higher than that under six-line full load. When under three-line eccentric load， the stress of arch rib is the most disadvantageous. However， the displacement and stress of the arch rib meet the requirements of the code， and the safety of the arch rib can be guaranteed in the use stage. The influence of temperature on the displacement of arch rib is analyzed. The vertical displacement of each part of arch rib changes in a parabolic shape. With the increase of the distance between arch rib and arch foot， the value of vertical displacement increases and reaches the maximum value at the arch top. The relationship between the displacement of arch rib and temperature is fitted， which provides a relevant basis for predicting the temperature deformation of six-line simply supported steel box composite arch bridge. At the same time， the vertical displacement of the arch roof at different temperatures is analyzed when the stiffness ratio of the arch rib to the main beam is changed. The vertical displacement of the arch rib can be reduced by increasing the stiffness of the arch rib.

Key words steel box overlap; arch rib; force analysis; temperature; stiffness ratio

0 引言

世界上第1座钢拱桥是1874年美国建造的跨越密西西比河的三跨钢桁架拱[1]。钢结构与混凝土结构相比，具有抗拉性能好、自重小等特点。近年来，随着科学技术的进步，作为大跨度桥梁形式之一的钢拱桥得到迅速发展，其跨径逐步增大，结构形式日新月异。

钢箱叠合拱桥作为一种结构新颖的钢拱桥，因跨越能力强、刚度大、造型美观、桥下净空较大等特点，被我国高速铁路桥梁建设所应用。甬台温铁路雁荡山特大桥为我国高速铁路中第1座钢箱叠合拱桥，其主跨采用下承式钢箱叠拱桥[2]。哈大高速铁路新开河特大桥釆用下承式钢箱叠拱，拱肋由上、下拱肋连接而成，上下拱肋之间设3道X型横撑[3]。

目前国内外对钢拱桥的研究主要集中于钢管拱桥、钢桁架拱桥及钢箱提篮拱桥等几种桥型。 2011年Chen等[4]对一座钢箱拱桥的力学性能进行了测试和研究，采用空间有限元分析软件MIDAS/Civil对模型桥各使用阶段的各工况进行了空间模拟研究;2014年刘德鹏等[5-6]以伊克昭大矢跨比钢箱拱桥为研究对象，对其拱肋起吊过程中的拱肋的整体稳定性进行了有限元分析;韩辉等[7]以重庆江津笋溪河钢箱-混凝土组合拱桥为研究对象，对其施工过程中整体温度变化和日照温度变化作用下的主拱应力、结构变形及温度场分布进行研究;2015年王林等[8]以超高矢跨比拱桥为研究对象，对其在风荷载和温度荷载作用下不同吊装过程中的拱肋稳定性进行了对比;2017年杨勇[9]以龙门黄河大桥为研究对象，分析了铁路钢箱提篮拱桥中各部分构件的受力敏感性。综上所述，钢箱叠合拱桥在高速铁路中应用的时间相对较短且实际工程案例相对较少，缺乏相关的理论指导和技术支持。同时，钢箱叠合拱桥的拱肋在施工过程中受力情况复杂多变，因此，研究拱肋的受力性能对施工的成败具有重要意义。

1 工程概况

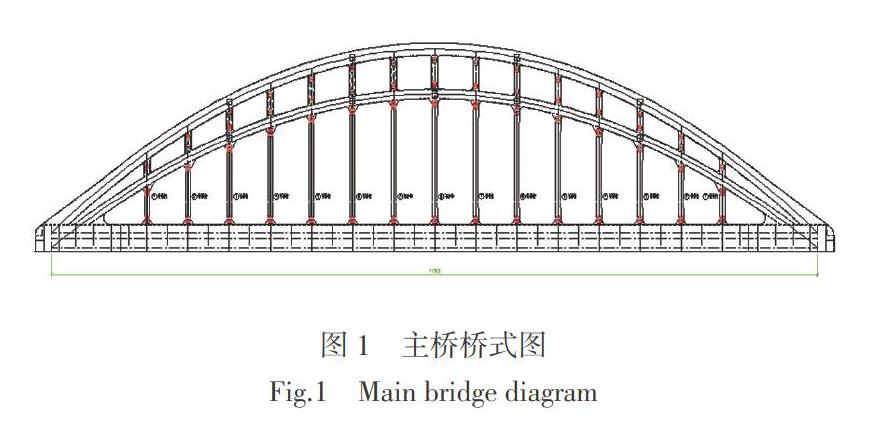
北京铁路枢纽丰台站扩能改造工程，在北京丰台区跨越四环路框构;跨越方式采用计算跨径112 m钢箱叠合拱桥，桥梁结构采用刚性系梁、刚性拱的结构形式，梁端采用牛腿与相邻跨简支板搭接，简支拱含牛腿全长116.68 m，桥梁布置六线铁路，桥宽38.6 m，双主拱结构，如图1所示。

本文以此六线简支钢箱叠合拱桥为工程背景，利用MIDAS/Civil建立有限元模型，通过对其拱肋的受力特性分析，指导施工;本桥属国内首例，将为日后钢箱叠合拱桥在高速铁路中的设计应用提供相关经验。

2 有限元模型

六线简支钢箱叠合拱桥拱肋轴线采用抛物线，上拱肋矢跨比f/l = 1∶4.571，拱轴方程为：[y1=-24.5（x1-][56）2/562+24.5]，下拱肋矢跨比f/l = 1∶5.463，拱轴方程为：[y2=-20.5（x2-56）2/562+20.5]。拱桥两拱肋平行布置，拱肋采用上、下拱组成的叠拱形式，上下拱肋横截面均为等高度钢箱矩形，上拱肋截面内高、宽均为1.6 m，下拱肋内高1.2 m，内宽1.6 m。

利用MIDAS/Civil建立六线简支钢箱叠合拱桥的空间有限元模型，其中将上下拱肋、竖杆、横撑、纵梁与横梁以及端梁采用梁单元模拟，吊杆采用桁架单元模拟，桥面板、轨道等按照恒载施加在横梁上;外部约束条件按照实际桥梁中支座对于桥梁的约束作用进行模拟，如表1所示。

全橋有限元模型共计1 513个节点、 2 278 个单元，其中梁单元 1 415个，桁架单元 188 个。

六线简支钢箱叠合拱桥的空间有限元模型如图2所示。

桥梁的价值主要体现在使用阶段，为了确保六线简支钢箱叠合拱桥在使用阶段的安全性，有必要对其在使用阶段的结构受力情况进行分析，车道分布情况如图3所示，主要分以下几种工况，如表2所示。

3 拱肋受力分析

3.1 拱肋位移分析

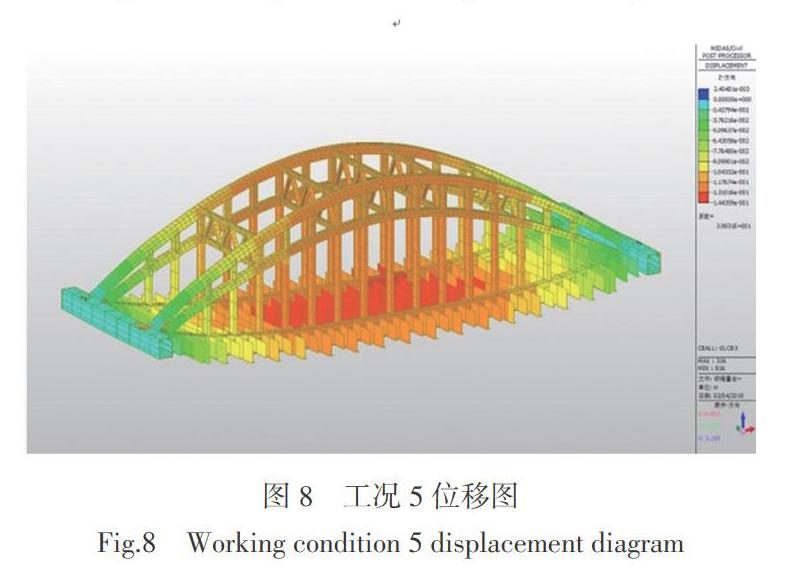
工况1至工况5下的拱肋竖向位移图如图4 ～ 图12所示。

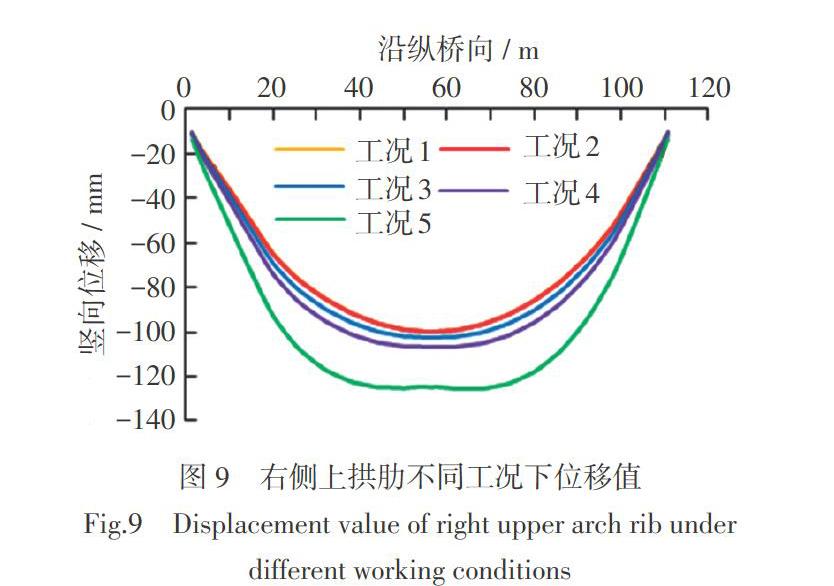
从图9可以看出，对于右侧上拱肋位移随着荷载的增加，位置值增大，在6线全载作用下位移值达到124.7 mm，6线全载情况下的上拱肋位移值比自重作用下增加24.9 mm;在1线偏载情况下，位移值与自重荷载下相比，没有增加;在2线偏载情况下，位移值与自重荷载下相比，增加2.8 mm;在3线偏载情况下，位移值与自重作用下相比，增加6.7 mm。

从图10可以看出，对于左侧上拱肋位移，随着偏载的增加，位移值也增加，在3线偏载作用下位移值达到最大值128.8 mm，在6线全载作用下，位移值稍微有点减小，与3线偏载作用下的位移值减小3.7 mm。在1线偏载情况下，位移值与自重荷载下相比，增加20 mm;在2线偏载情况下，位移值与自重荷载下相比，增加28.3 mm。

从图11可以看出，对于右侧下拱肋位移随着荷载的增加，位置值增大，在6线全载作用下位移值达到125.1 mm，6线全载情况下的上拱肋位移值比自重作用下增加25 mm;在1线偏载情况下，位移值与自重荷载下相比，没有增加;在2线偏载情况下，位移值与自重荷载下相比，增加2.9 mm;在3线偏载情况下，位移值与自重作用下相比，增加6.8 mm。

从图12可以看出，对于左侧下拱肋位移，随着偏载的增加，位移值也增加，在3线偏载作用下位移值达到最大值129.3 mm，在6线全载作用下，位移值稍微有点减小，与3线全载作用下的位移值减小3.7 mm。在1线偏载情况下，位移值与自重荷载下相比，增加19.7 mm;在2线偏载情况下，位移值与自重荷载下相比，增加28.1 mm。

从图4～图12中可以看出，在不同工况作用下，拱肋的竖向位移形状符合抛物线形状。在自重以及6线全载作用下，左右拱肋产生的位移相差很小，

左侧拱肋位移值比右侧位移值大0.5 mm，由于差值很小，可以忽略，认为左右拱肋在对称荷载作用下的位移值相同。

从图14和图16对比中可以看出，右上拱肋下缘最大压应力在1线偏载情况下为27.9 MPa，在2线偏载情况下为28.5 MPa，在3线偏载情况下为31.4 MPa，右上拱肋下缘最大压应力比左上拱肋下缘最大压应力分别减小4.7 MPa、4.1 MPa、5.6 MPa。

从图17和图19对比中可以看出，右下拱肋上缘最大压应力在1线偏载情况下为148 MPa，在2线偏载情况下为155 MPa，在3线偏载情况下为164 MPa，右下拱肋上缘最大压应力比左下拱肋上缘最大压应力分别减小36 MPa、46 MPa、44 MPa。

从图18和图20对比中可以看出，右下拱肋下缘最大压应力在1线偏载情况下为8.3 MPa，在2线偏载情况下为10.3 MPa，在3线偏载情况下为14.1 MPa，右下拱肋下缘最大压应力比左下拱肋下缘最大压应力分别减小13.3 MPa、17.0 MPa、16.4 MPa。

从图13～图20中可以看出，在不同工况作用下，上下拱肋的上下缘应力均为压应力。在自重以及6线全载作用下，左右拱肋产生的应力相差很小，左侧拱肋应力值比右侧应力值大0.3 MPa以内，由于差值很小，可以忽略，认为左右拱肋在對称荷载作用下的应力值相同。由于竖杆、吊杆的影响，拱肋应力呈现有规律的波浪形状。此外，在3线偏载作用下，拱肋压应力最大，对拱肋受力最不利。左右上下拱肋在5种工况下产生的压应力均小于Q370qE钢材的屈服应力值，满足规范要求。

4 温度对拱肋的影响因素分析

在对结构进行受力分析时，温度是不可忽略的一个重要因素，由于钢箱拱桥中各个构件的温度梯度较小，因此各构件在温度梯度影响下的受力和变形可以忽略不计，因此只考虑整体升温或降温对各个构件受力的影响。由于六线简支钢箱拱桥施工在5月份左右，桥址所处地区在5月份昼夜温差较大，因此需要考虑温度对各个构件的受力及变形的影响，由于钢箱拱采用Q370qE钢材，考虑温度对其应力的影响实际意义不大，因此只进行温度对拱肋变形的影响分析。本文仅分析拱肋在成桥状态下温度对拱肋变形的影响。

以拱肋在0 ℃时的位移作为基准点，分析不同温差下的拱肋位移变化情况，上拱肋在不同温差下的竖向位移变化如图21所示。

从图21中可以看出，在相同温度下，拱肋竖向位移变化呈抛物线形，随着拱肋与拱脚之间距离的增加，竖向位移值增大，在拱顶处达到最大值;升温5 ℃与降温5 ℃、升温10 ℃与降温10 ℃、升温15 ℃与降温15 ℃的竖向位移变化值相反，呈对称关系，说明当温差绝对相等时，拱肋竖向位移变化曲线具有对称性，即拱肋竖向位移变化值的绝对值相等。随着温度的升高，温差越大，拱肋竖向位移变化值越大，且随着拱肋与拱脚之间距离的增加，变化越明显，在拱顶处变化值最大。当温差达到35 ℃时，拱肋竖向位移变化可达到11.8 mm。

下拱肋在不同温差下的竖向位移变化如图22所示。

从图22中可以看出，下拱肋与上拱肋的竖向位移变化具有相同的规律，在相同温度下，拱肋竖向位移变化呈抛物线形，随着拱肋与拱脚之间距离的增加，竖向位移值增大，在拱顶处达到最大值;当温差绝对相等时，拱肋竖向位移变化曲线具有对称性，即拱肋竖向位移变化值的绝对值相等;随着温度的升高，温差越大，拱肋竖向位移变化值越大，且随着拱肋与拱脚之间距离的增加，变化越明显，在拱顶处变化值最大。当温差达到35 ℃时，拱肋竖向位移变化可达到8.8 mm。

从图21和22的对比中可以发现，温度变化对上拱肋位移产生的影响要大于对下拱肋的影响，且随着与拱脚之间距离的增加，影响越明显，在拱顶处达到最大。

由于六线简支钢箱拱桥的拱肋为分节段进行拼装，当2个半跨钢箱拱拱肋合拢时，需要调整拱肋的线形，此时主要调整的是拱顶的标高，因此对上下拱肋在拱顶处的竖向位移变化值与温差之间的关系曲线进行拟合，如图23所示。

从图23中可以看出，拱顶处的竖向位移与温差近似成正比例关系，其中上拱肋拱顶位移与温差的关系式为

y = 0.337 7x。                           （1）

下拱肋拱顶位移与温差的关系式为

y = 0.251 3x。                            （2）

考虑上拱肋与主梁刚度比变化在不同温差下对拱肋位移的影响，上拱肋抗弯刚度与主梁抗弯刚度变化情况分为以下几种工况，如表3所示。

上拱肋抗弯刚度与主梁抗弯刚度变化时拱顶在不同温差下的上拱肋竖向位移变化如图24所示。

从图24中可以看出，工况1～工况5情况下，上拱肋拱顶位移与正常刚度比下的上拱肋拱顶在不同温度下的位移相比，位移变化值分别约为-4.3 mm、2 mm、1.9 mm、3.6 mm、5.3 mm。在相同温度下，上拱肋与主梁刚度比减小，拱顶位移增加，且刚度比减小越大，拱顶位移增加值越大;上拱肋与主梁刚度比增加，拱顶位移减小，且刚度比增加越大，拱顶位移减小值越大。

上拱肋抗弯刚度与主梁抗弯刚度变化时拱顶在不同温差下的下拱肋竖向位移变化如图25所示。

从图25中可以看出，工况1～工况5情况下，下拱肋拱顶位移与正常刚度比下的下拱肋拱顶在不同温度下的位移相比，位移变化值分别约为  -3.6 mm、-1.6 mm、2.3 mm、4.1 mm、5.7 mm。在相同温度下，上拱肋与主梁刚度比减小，拱顶位移增加，且刚度比减小越大，拱顶位移增加值越大;上拱肋与主梁刚度比增加，拱顶位移减小，且刚度比增加越大，拱顶位移减小值越大。

从图24与图25中可以看出，温度相同，上拱肋与主梁刚度比减小对上拱肋拱顶位移的影响要稍大于对下拱肋拱顶位移的影响，差值为0.4 mm;上拱肋与主梁刚度比增加对上拱肋拱顶位移的影响要稍小于对下拱肋拱顶位移的影响，差值为0.4 mm。相同温度下，上拱肋与主梁刚度比变化对拱顶位移的影响如图26所示。

从图26中可以看出，相同温度下，上拱肋与主梁刚度比变化值与拱顶位移变化值成正比例关系。

考虑上拱肋与主梁刚度比变化在不同温差下对拱肋位移的影响，上拱肋抗弯刚度与主梁抗弯刚度变化情况分为以下几种工况，如表4所示。

下拱肋抗弯刚度与主梁抗弯刚度变化时上拱肋在不同温差下的拱顶竖向位移变化如图27所示。

从图27中可以看出，工况1～工况5情况下，上拱肋拱顶位移与正常刚度比下的上拱肋拱顶在不同温度下的位移相比，位移变化值分别约为-1.1 mm、-0.5 mm、0.6 mm、1.1 mm、1.6 mm。在相同温度下，下拱肋与主梁刚度比减小，拱顶位移增加，且刚度比减小越大，拱頂位移增加值越大;下拱肋与主梁刚度比增加，拱顶位移减小，且刚度比增加越大，拱顶位移减小值越大。

下拱肋抗弯刚度与主梁抗弯刚度变化时下拱顶在不同温差下的拱顶竖向位移变化如图28所示。

从图28中可以看出，工况1～工况5情况下，下拱肋拱顶位移与正常刚度比下的下拱肋拱顶在不同温度下的位移相比，位移变化值分别约为-1.1 mm、-0.5 mm、0.5 mm、1.0 mm、1.5 mm。在相同温度下，下拱肋与主梁刚度比减小，拱顶位移增加，且刚度比减小越大，拱顶位移增加值越大;上拱肋与主梁刚度比增加，拱顶位移减小，且刚度比增加越大，拱顶位移减小值越大。

从图27与图28中可以看出，温度相同，下拱肋与主梁刚度比减小对上下拱肋拱顶位移的影响基本一致，相同温度下，下拱肋与主梁刚度比变化对拱顶位移的影响如图29所示。

从图29中可以看出，相同温度下，下拱肋与主梁刚度比变化值与拱顶位移变化值成正比例关系。

从图26与图29对比中可以看出上拱肋与主梁刚度比变化对拱顶位移的影响要大于下拱肋与主梁刚度比变化对拱顶位移的影响。

5 结论

1）利用MIDAS/Civil建立六线简支钢箱叠合拱桥有限元模型对其拱肋的受力特性分析，能够判定应力状态能否满足规范要求，指导施工。

2）利用MIDAS/Civil建立六线简支钢箱叠合拱桥的空间有限元模型，针对使用阶段的结构受力情况，分别进行拱肋位移分析和拱肋应力分析，计算各种工况下产生的应力小于结构材料应力值，能够满足规范要求。

3）拟合出了上下拱肋拱顶位移与温差的关系，可以为预测拱肋的温度变形提供相关依据。

4）上拱肋与主梁刚度比变化对拱顶位移的影响要大于下拱肋与主梁刚度比变化对拱顶位移的影响，增加拱肋刚度，可以减小拱肋竖向位移。

参考文献：

[1]    陈宝春，陈康明，赵秋. 中国钢拱桥发展现状调查与分析[J]. 中外公路，2011，31（2）：121-127.

[2]    阮正洁，齐金朋. 甬台温铁路雁荡山特大桥2×90 m叠合拱钢桥施工技术[J]. 铁道标准设计，2010（3）：57-62.

[3]    张坤，雷俊卿，曹珊珊. 高速铁路钢箱叠合拱桥结构设计参数影响性研究[J]. 世界桥梁，2014，42（4）：68-73.

[4]    CHEN Q，LIU L Y. Research on mechanical property test of CFRP hanger in steel box arch bridge[J]. Advanced Materials Research，2011，255/256/257/258/259/260：3070-3076.

[5]    刘德鹏. 受风和温度影响的大矢跨比钢箱拱桥施工方案及控制技术[D]. 镇江：江苏科技大学，2014.

[6]    刘德鹏，王林，彭鑫. 风荷载效应作用下大矢跨比钢箱拱肋吊装过程稳定性分析[J]. 江苏科技大学学报（自然科学版），2014，28（2）：125-130.

[7]    韩辉，吕娜，周志祥，等. 钢箱混凝土组合拱桥施工过程中温度效应分析[J]. 重庆交通大学学报（自然科学版），2014，33（6）：27-33.

[8]    王林，邢朝伟，王芳. 超高矢跨比拱桥拱肋吊装稳定性分析[J]. 武汉理工大学学报（交通科学与工程版），2015，39（4）：725-728.

[9]    杨勇. 铁路提篮拱桥设计参数及构造敏感性分析研究[D]. 成都：西南交通大学，2017.

[10]  TB 3466-2016，铁路荷载图示[S].

[责任编辑    杨    屹]