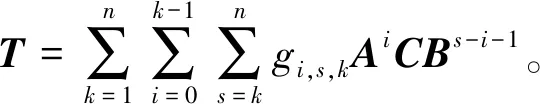陈佳宏，邓 勇

(喀什大学 数学与统计学院，新疆 喀什 844006)

设K是一个域，用Μn,m(K)(Μn(K))表示域K上的全体n×m(n×n)矩阵环。令A∈Μn(K)，B∈Μm(K)，C∈Μn,m(K)。方程

AX-XB=C

(1)

称为Sylvester矩阵方程，其中X∈Μn,m(K)。在式(1)中，当C=O时，即

AX-XB=O

(2)

称为对应于式(1)的齐次矩阵方程;特别地，当B=-AT时，即

AX+XAT=C

(3)

称为Lyapunov矩阵方程。

在控制论、信号处理、神经网络、模型降阶、图像恢复等领域经常会涉及到Sylvester矩阵方程的数值求解问题。关于Sylvester矩阵方程的求解和数值计算，目前已有很多讨论[1-9]。例如，文献[2]讨论了Lyapunov矩阵方程的公共解，给出了其无公共解的一个充要条件；文献[3]利用Jordan标准形和最小多项式理论，讨论了Lyapunov矩阵方程有非零解的充要条件，并得到其非零解空间的维数定理；文献[4]利用四元数矩阵的实分解和循环矩阵的特定结构，借助Kronecker积，得到了四元数体上Sylvester矩阵方程循环解的存在条件及其通解形式；文献[5]给出了Sylvester矩阵方程的一种基于梯度的迭代算法；文献[6]改进了传统的梯度迭代法，给出了求解Sylvester矩阵方程的松弛梯度迭代法，有效地提高了收敛速度。

本文利用Sylvester算子的性质，给出了Sylvester矩阵方程(1)在任意域K上的可解性判定，并介绍求其多项式解的一般形式的一种新方法。

1 Kronecker乘积

1.1 Vec算子

显然，Vec(X)是一个nm维列向量，并且对∀X,Y∈Μn,m(K)，有Vec(X+Y)=Vec(X)+Vec(Y)。

1.2 Kronecker乘积

定义2[10]设X∈Μn,m(K)，Y∈Μp,q(K)。定义矩阵X和Y的Kronecker乘积为

式中，xij是矩阵X的(i,j)元。显然，X⊗Y是(np)×(mq)矩阵。

定理1[10]设矩阵X,Y,Z的乘积XYZ有定义。于是，Vec(XYZ)=(ZT⊗X)Vec(Y)。

1.3 Kronecker乘积的应用

设In表示n阶单位矩阵。利用Kronecker乘积，可将Sylvester矩阵方程改写为

(Im⊗A-BT⊗In)Vec(X)=Vec(C)

(4)

的形式。事实上，由AX-XB=C，有Vec(AX-XB)=Vec(C)或Vec(AX)-Vec(XB)=Vec(C)。因此，Vec(AXIm)-Vec(InXB)=Vec(C)。再由定理1可得

(Im⊗A)Vec(X)-(BT⊗In)Vec(X)=Vec(C)或(Im⊗A-BT⊗In)Vec(X)=Vec(C)。

2 Sylvester算子

设K是任意一个域，多项式f,g∈K[x]。用gcd(f,g)和res(f,g)分别表示f和g的最大公因式和结式；用pA表示方阵A的特征多项式；mA表示A的最小多项式。

定义3 设A∈Μn(K)，B∈Μm(K)。线性变换

ψ(A,B):Μn,m(K)→Μn,m(K),TAT-TB

称为关于矩阵A和B的Sylvester算子。

记φA:Μn,m(K)→Μn,m(K),TAT和TB

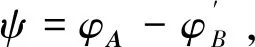
定义4 称C(A,B)={T∈Μn,m(K)|AT=TB}为矩阵A和B的Sylvester(或中心化子)空间[11]。

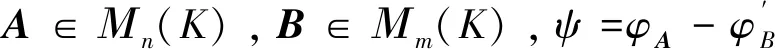
(i)f(φA)=φf(A);

证明对自然数k和矩阵T∈Μn,m(K)，分别有

(iii)ψ(T·f(B))=ψ(T)f(B)

成立，所以定理2正确。

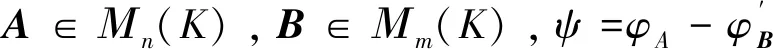
成立。

3 引理

记号同前，引入以下引理：

引理1 设A∈Μn(K)，B∈Μm(K)。下列陈述等价:

①算子ψ(A,B)=ψ是同构的;

②C(A,B)={O};

③在K[x]中，pA和pB无公共的素因式;

④pA和pB的结式res(pA,pB)≠0;

⑤mA和mB的结式res(mA,mB)≠0。

证明参见文献[12]，在此从略。

引理2 式(1)的通解可表示为其特解和式(2)的通解之和。

证明设X和X0是式(1)的通解和特解，即

于是，有A(X-X0)-(X-X0)B=O，即(X-X0)是式(2)的通解。故式(1)的通解可表示为其特解和式(2)的通解之和。

引理3[13]设f∈K[x]是一个n次多项式，x是域K上的未定元。于是

1)对所有0≤k≤n，都有Δkf(x)∈K[x];

2)k!Δkf(x)=f(k)(x)，其中f(k)(x)是f(x)的k阶导数。

4 Sylvester矩阵方程的可解性

4.1 可解性判定

设K是一个代数闭域，A∈Μn(K)，B∈Μm(K)。用σ(A)表示矩阵A的所有特征值集合(谱)。文献[3]指出，C(A,B)={O}⟺σ(A)∩σ(B)=∅。下面，将此结论推广到任意域K上，即

定理3 Sylvester矩阵方程(1)有唯一解⟺pA和pB无公共的素因式。

证明首先，式(1)有唯一解⟺关于A和B的Sylvester算子同构[11-12]。然后，利用引理1即可得证。

推论2pA和pB无公共的素因式⟺mA和mB无公共的素因式。

推论3 式(1)的解空间是一个仿射空间，并且维数等于dimKC(A,B)。

推论4 式(1)有唯一解⟺式(2)有唯一解并且为零。

4.2 多项式解

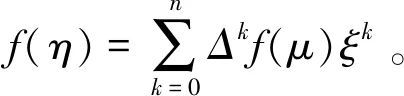
证明因μ=η-ξ，故有η=ξ+μ。在上述f(x+y)的表达式中，用μ代替x，ξ代替y后即可推出结果。

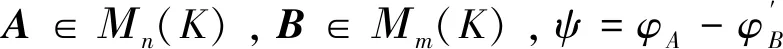
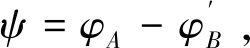
定理5 设A∈Μn(K)，B∈Μm(K)，ψ是关于A和B的Sylvester算子。若矩阵A和B的特征多项式无公共的素因式，则

(a)ψ是一个同构。

证明(a)由引理1即可得证。

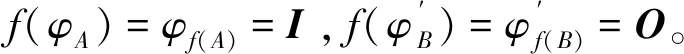
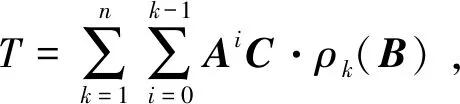
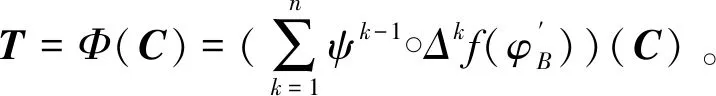
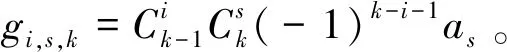
于是，有