戴 伟①

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

调和平均值、算术平均值、几何平均值和平方平均值之间的关系就是均值不等式，这些均值不等式是不等式研究的重要内容之一，被广泛应用到许多数学领域. 文献［1］介绍初等不等式

其中fi:E→R(E⊂R,i=1,2,…,n). 文献［2］推导算术平均值和几何平均值的关系，以及对数平均值和某些其他平均值之间的关系. 文献［3］用初等不等式（1）证明一些不等式和微积分中的一些基本结论.Chen［4］用初等不等式（1）证明算术—几何平均不等式，以及柯西不等式和三角不等式. 关于更多不等式的一些结果参见文献［5-15］.

本文首先利用初等不等式（1）证明一个新的不等式，然后利用这个不等式和一些已知不等式推导出调和—几何—算术—平方平均不等式，以及调和平均值的下界和平方平均值的上界，并给出平均不等式在酉矩阵中的应用.

1 主要结论

利用初等不等式（1）给出一个新的不等式，再利用该不等式推出调和—几何—算术—平方平均不等式，以及调和平均值的下界和平方平均值的上界.

定理1 若ai,bi ＞0,p,q是任意实数，则

其中等号成立的充要条件是aibj=ajbi(i,j=1,2,…,n).

证明设这里α ＞0,ai,bi ＞0(i=1,2,…,n)，则

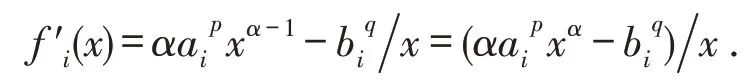
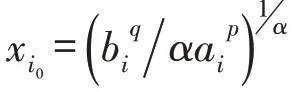
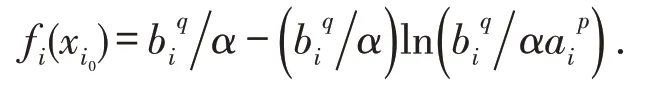
令f′i(x)=0，得，因此，函数fi(x)在点xi0处取得最小值，即

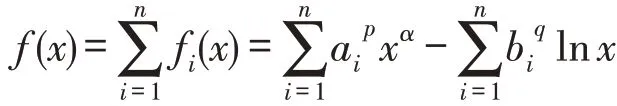
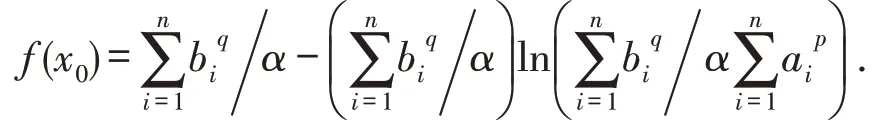
由式（1）得

即

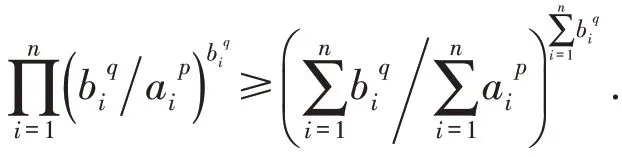
显然，上式等号成立的充要条件是xi0=xj0(i,j=1,2,…,n)，即aibj=ajbi(i,j=1,2,…,n).

根据定理1中不等式（2），可得以下不等式. 令p=1,q=1，得文献［3］中的不等式

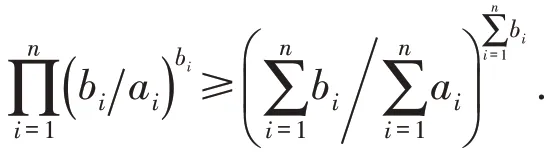
令p=-1,q=1,bi=1，得调和—几何平均不等式

其中ai ＞0(i=1,2,…,n). 显然，式（3）等式成立的充要条件是ai=aj(i,j=1,2,…,n).

令p=1,q=1,bi=1，得几何—算术平均不等式

其中ai ＞0(i=1,2,…,n). 显然，式（4）等式成立的充要条件是ai=aj(i,j=1,2,…,n).

令p=1,q=-1,ai=1，得调和平均不等式的下界

其中bi ＞0(i=1,2,…,n). 显然，式（6）等式成立的充要条件是bi=bj(i,j=1,2,…,n).

文献［3］给出下列不等式.

在式（7）中，令α1=2,α2=1，得算术—平方平均不等式

其中ai ＞0(i=1,2,…,n). 显然，式（8）等式成立的充要条件是ai=aj(i,j=1,2,…,n).根据式（3）～（8）得

其中ai ＞0(i=1,2,…,n). 并且式（9）中等式成立的充要条件是ai=aj(i,j=1,2,…,n).

2 应用举例

最后，利用均值不等式（9），证明酉矩阵的一个充要条件. 下面介绍矩阵分析的相关概念. 设Mn表示n阶复方阵的集合和Un表示n阶酉矩阵的集合. 对于A ∈Mn，将A ∈Mn的奇异值按降序排列s1≥s2≥…≥sn. 显然谱范数‖ ‖A∞=s1，迹范数‖ ‖A1=s1+s2+…+sn. A 的数值半径定义为

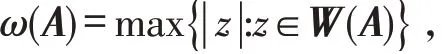
若A ∈Un，则A-1=A∗，A 是一个正规矩阵且ω(A)=‖ ‖A∞.

首先，先给出一个引理.

引理2［5］若A ∈Mn，则ω(A)≤‖ ‖A1≤nω(A).

定理3 若A ∈Mn，则A 是酉矩阵的充要条件是ω(A)≤1和ω(A-1)≤1.

证明因为A 是酉矩阵，所以A-1=A*和A 是正则矩阵，因此

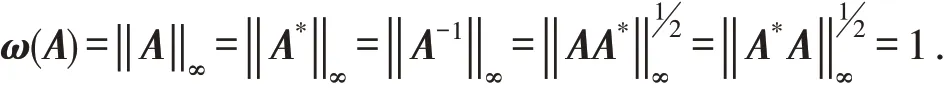
反过来，考虑A-1,A*的奇异值分解，存在U,V ，使得

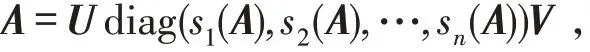
和

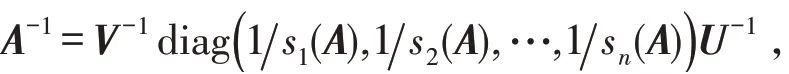
其中s1(A)≥s2(A)≥…≥sn(A)≥0.

下面证明s1(A)=s2(A)=…=sn(A)=1. 事实上，由引理2得

和

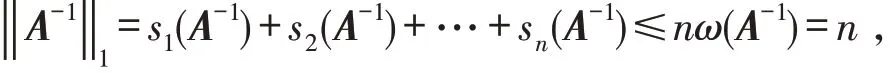
即

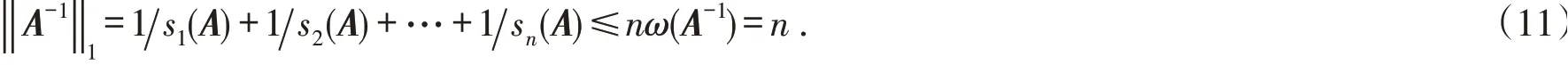
因此，由式（10）和式（11）可得

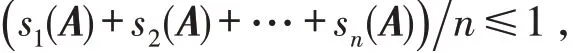
和

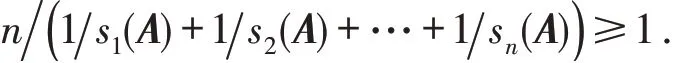
根据式（9）得显然，等号成立，故此s1(A)=s2(A)=…=sn(A)=1.

注1 文献［16］给出无限维希尔伯特空间上酉算子上述结果的刻画. 需要指出，定义在无限维希尔伯特空间上酉算子不一定存在奇异值，本文证明思路和方法与文献［16］完全不同.