☉重庆市万州高级中学 张 进

一、试题呈现

（2018年龙东中考题）如图，在Rt△BCD中，∠CBD=90°，BC=BD，点A在CB的延长线上，且BA=BC，点E在直线BD上移动，过点E作射线EF⊥EA，交CD所在直线于点F.

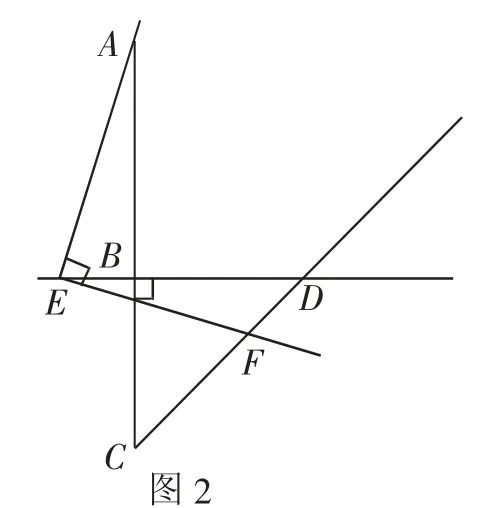
（2）当点E在直线BD上移动时，如图2、图3所示，线段BC、DE与DF又有怎样的数量关系？请直接写出你的猜想，不需证明.

二、思路探究

三、解法探究

1.关于第（1）问的解法探究

思路1：利用直角，构“三垂直”.

证法1：如图4，过点F作FG⊥BD于点G.

所以∠EGF=∠ABE=90°，则∠BAE+∠AEB=90°.

因为EF⊥EA，所以∠GEF+∠AEB=90°.

所以∠BAE=∠GEF.

因为BC=BD，BA=BC，所以AB=BD.

因为∠CBD=90°，BC=BD，所以∠CDB=∠FDG=45°，则

思路2：洞察结构，构“辅助圆”.

证法2：如图5，连接AD、AF.

因为BC=BD，BA=BC，∠CBD=90°，所以△CBD、△ABD均为等腰直角三角形，则∠ADF=90°.又因为EF⊥EA，所以A、E、D、F四点共圆，⊙O的圆心O即为AF的中点，所以∠EAF=∠CDB=∠BAD=45°，即∠BAE+∠EAD=∠EAD+∠DAF，所以∠BAE=∠DAF.

思路3：巧妙截取，构造全等.

证法3：如图6，在AB上截取AG=ED，连接EG.

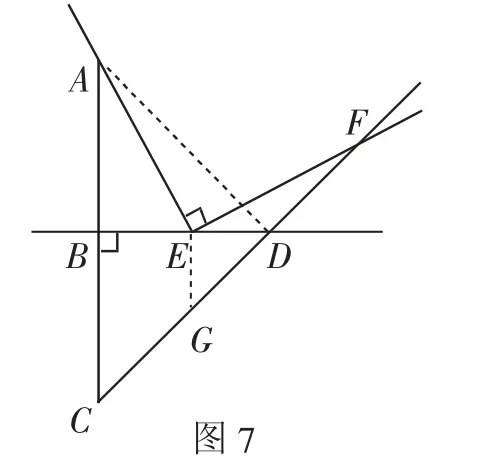
证法4：如图7，连接AD，过点E作EG⊥BD交CD于点G.

证法5：如图8，连接AD，过点E作EG⊥BD交AD于点G.

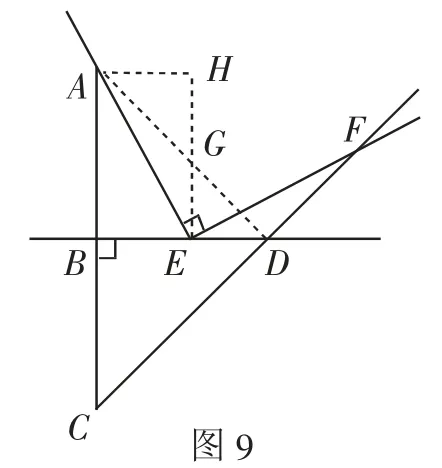
证法6：如图9，连接AD，过点E作EG⊥BD交AD于点G，过点A作AH⊥EG交EG的延长线于点H.

思路4：巧妙对称，构造等腰.

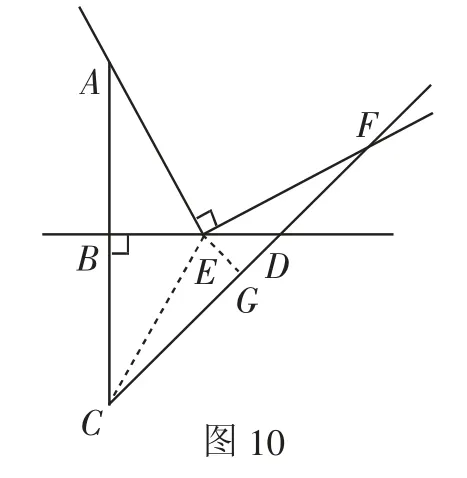
证法7：如图10，过点E作EG⊥CD于点G，连接CE.

易证△EGD、△CBD为等腰直角三角形，然后证明△ABE△CBE（SAS），再证△ECG△EFG（AAS），则FG=CG.

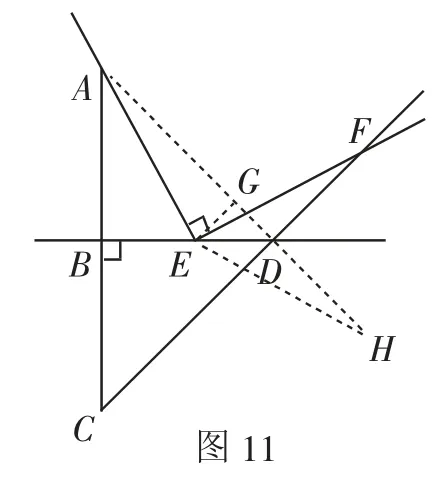
证法8：如图11，连接AD并延长至点H，使DH=FD，连接EH，过点E作EG⊥AH于点G.

证法9：如图12，连接AD并延长至点G，使DG=FD，连接EG、FG.

思路5：巧妙旋转，构“特殊形”.

证法10：如图13，在BC上截取BG=BE，连接EG、DG.

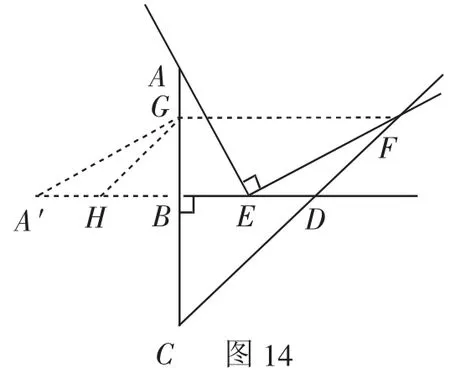
证法11：如图14，过点F作FG∥BD交AB于点G，过点G作GA′∥EF交DB的延长线于点A′，过点G作GH∥FD交A′B于点H.

证法12：如图15，过点D作DG⊥BD，使DG=ED，连接EG、AD，过点G 作GH∥AE交AD于点H.

证法13：如图16，连接AD，过点E作EG⊥AD于点G，过点E作EH⊥CD于点H.

证法14：如图17，过点A作AM⊥AB，过点D作DM⊥BD于点D，在AM上截取MG=MN，连接DG、NG.

思路6：用代数法，求解直角三角形.

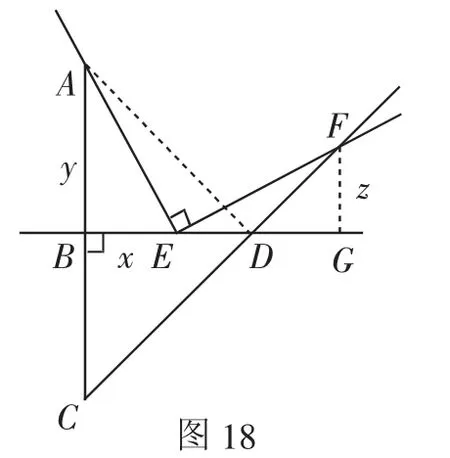
证法15：如图18，过点F作FG⊥BD于点G，连接AD.

因为EF⊥EA，所以∠DEF+∠AEB=90°.又∠BAE+∠AEB=90°，所以∠BAE=∠DEF，则tan∠BAE=tan∠GEF，所以，整理得（y-x）（x-z）=0.因为y≠x，所以x=

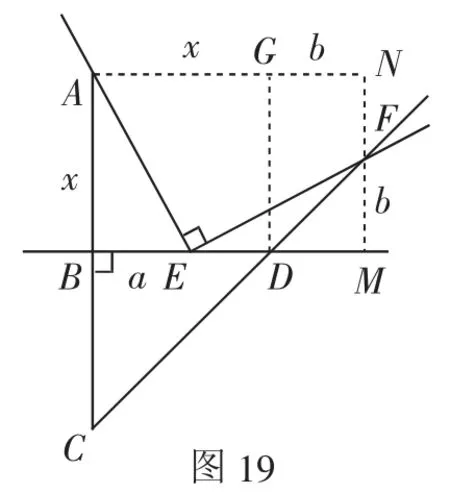
证法16：如图19，连接AF，过点F作MF⊥BD于点M，过点A作AN⊥AB交MF的延长线于点N，过点D作DG⊥AN于点G.

可得矩形ABMN和正方形ABDG.

设AB=x，BE=a，FM=DM=GN=b，则FN=x-b，EM=x+b-a.

根据勾股定理，可得AF2=AE2+EF2，AE2=AB2+BE2，EF2=EM2+FM2，AF2=AN2+FN2，所以（x+b）2+（x-b）2=（x+b-a）2+b2+x2+a2，整理并化简得a=b，即BE=FM=DM，所以

2.关于第（2）问图2、图3的解法探究

借用第（1）问的解题方法，采用类比推理的办法可探究图2的结论为图3的结论为BC+限于篇幅，不再赘述.

四、教学启示

1.提倡一题多解，开阔解题视野

几何压轴题教学时，教师要深刻理解问题结构和图形结构的变化情况，要善于抓住题目中的条件特征、数字特征、结论特征和图形特征，从中寻找解题突破口，联系相关知识点和解题方法，就可以得到不同的解法，这就是数学上常说的一题多解.数学解题教学中，教师应该有意识地针对一些典型的课本习题、中考试题，引导学生尝试运用不同的方法去解决，有利于沟通知识的内涵和外延，寻找自然解法.一题多解的目的并不在于“多解”，而在于培养学生思维的灵活性和层次性，这样就可以拓宽学生的解题思路，克服思维定式，培养学生的求异思维能力，开阔学生的解题视野.

2.学会类比推理，提高解题效率

三角形和四边形是初中数学的重要考点，在数学解题过程中，有很多几何压轴题可通过类比推理的方法解决，以达到高效、快捷的效果，激活学生思维，提高解题效率.类比推理是根据两个对象之间的形同和相似进行推理论证的一种重要数学思想方法，是中学数学解题中的重要方法之一，通过类比推理能够寻求解决同类问题的思路，可让模糊的问题清晰化、复杂的问题简单化、隐性的问题显性化.初中数学内容广泛，很多内容如代数问题、几何问题、方程和函数问题都需要用到类比推理.类比推理是一种行之有效的数学解题方法，在初中数学中大胆运用类比推理，不但可以达到温故而知新的目的，而且可以培养学生的灵活性思维，使复杂、抽象的数学问题简单化，从而大大提高解题的效率和速度.

3.构建基本模型，提升数学素养

在平时的解题教学中，教师帮助学生提炼总结出一些常见的几何基本模型，并运用这些基本模型解题，不仅有助于激发学生的学习兴趣，提高解题效率，而且对发展数学思维能力、培养创新意识具有重要的现实意义.重视基本模型解决几何题的一个基本套路，首先要认真分析条件，将条件与相关“基本模型”结合起来，利用这个“基本模型”的性质获得相关的结论，有时，背景图形中不一定有与条件匹配的“基本模型”，这时需要联想相关知识添加辅助线构造出相关的“基本模型”，再利用这个“基本模型”的性质，获取相应的结论，达到解决问题的目的.教师在平时教学中指导学生寻找解题思路，要熟悉基本模型，多总结、多积累、多识记、多联想、多应用，形成基本的解题能力，积累基本的数学活动经验，彻底脱离“题海战术”，努力提升学生的数学素养.