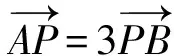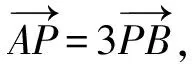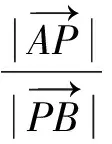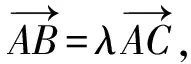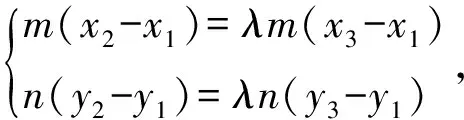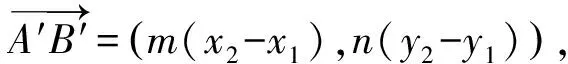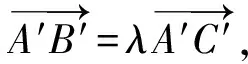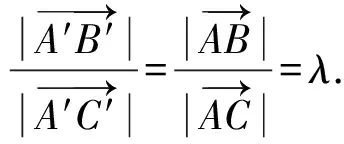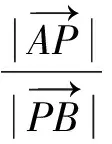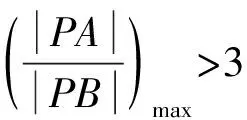一题之探——以数形结合思想为例
2019-05-24孙雪梅李德安
李 晶 孙雪梅 李德安
(1.曲靖市第一中学 655000; 2.曲靖师范学院数学与统计学院 655011)
数形结合思想是数学解题中常用的数学思想.华罗庚曾对数形结合思想有过精辟的论述:数与形,本是相倚依,焉能分作两边飞?数缺形时少直观,形少数时难入微. 数形结合百般好,隔离分家万事休.切莫忘,几何代数统一体,永远联系,切莫分离[1].“数”抽象而形式化,“形”具体而形象化.“数”与“形”对应的思维是分析性思维和视觉化思维,这两种思维在数学解题中都是必需的,它们在数学解题中相互作用互为补充.下面以2016年云南省第一次高中毕业生复习统一检测中的一道解析几何题的解答为例,说明如何通过对图形信息与数式信息的相互补充和交互作用的探究,引导学生探寻精彩而奇妙的解法.
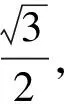
(1)求椭圆E的方程;
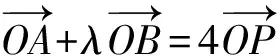
1 以数代形,常法开路
对(1)问,要求学生不作出图形,根据题设条件,用代数方法求出椭圆的方程,学生很容易想到用待定系数法和方程(组)的思想进行求解.
由已知得,

对(2)问,第一步必先求出λ的值.要确定λ的值,根据题设条件,学生会想到第一种途径:根据向量的运算求出λ的值.
向量的运算涉及“图”与“式”,既有视觉化思维,又涉及分析性思维,特别是对特殊情况的讨论,分析性思维尤为重要.
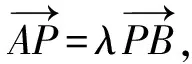
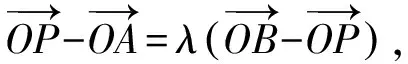
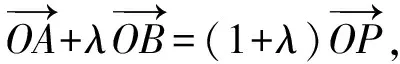
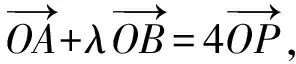
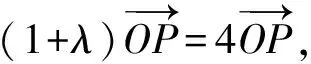
则1+λ=4,所以λ=3.
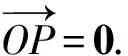
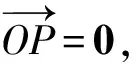
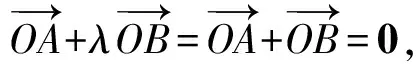
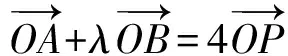
根据题设中的条件,有的学生还会想到第二种途径:利用定比分点向量公式求λ的值.有了前面的讨论和引导,学生会考虑解答的完整性,避免漏掉对特殊情况的讨论.
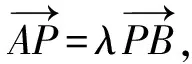
当O∉l时,由定比分点向量公式可得
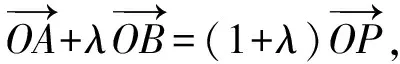
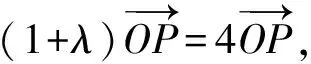
当O∈l时,即m=0时,也符合题意.
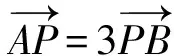
从“数或式”的角度,引导学生利用直线与圆锥曲线综合问题的通用解法:联立方程、消元、利用判别式“Δ”、韦达定理,可求得m的范围.
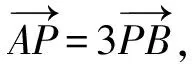
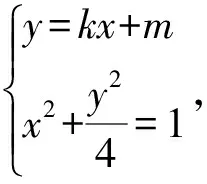
得(k2+4)x2+2mkx+m2-4=0,
Δ=4m2k2-4(k2+4)(m2-4)>0,
即k2-m2+4>0……①
设A(x1,y1),B(x2,y2),则由韦达定理得
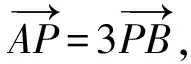
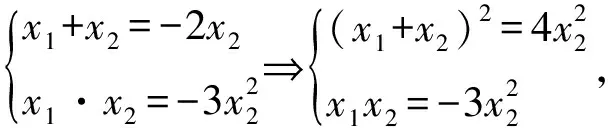
所以3(x1+x2)2+4x1x2=0,

化简得m2k2+m2-k2-4=0,
所以(m2-1)k2=4-m2,
当m2=1时,上式不成立,
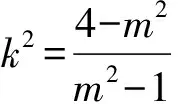
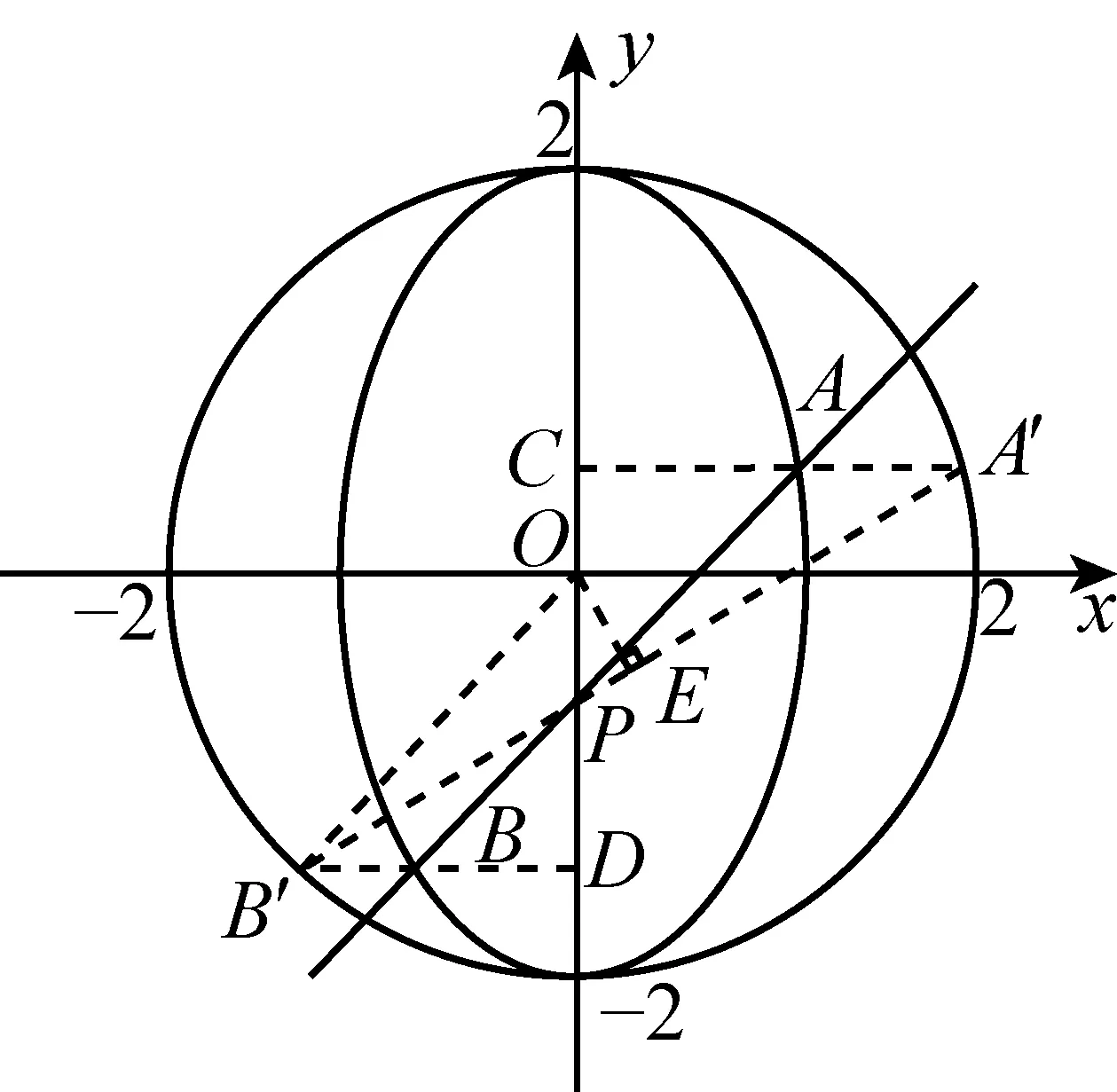
所以1 所以1 解法1从代数的角度找到解题的思路,虽然思路简单,容易理解,但涉及的代数运算较繁,容易计算出错. 解法2:设A(x1,y1),B(x2,y2), 4(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0 ② 所以3my2=2m2+4, 若m=0,上式显然不成立, 因为y2<2, (1)当m>0时,2m2-6m+4<0,解得1 (2)当m<0时,2m2+6m+4<0,解得-2 综上所述,m的取值范围是-2,-1∪1,2. 对第(2)问,解法1和解法2都是从“数或式”出发,利用常用的代数解法,求得m的取值范围,但解法2在解法1的基础上,利用整体思维,巧借m与y2的关系简化了运算过程,让学生在掌握常法的基础上,会去思考解法的进一步简化和优化. 引导学生以“形”助“数”,从几何的角度另辟蹊径,找到新的解法.点拨学生利用椭圆可由圆均匀压缩而得到,画出图形,看是否能从图中找到一些关系,或者从图形表征或题目信息中推导出更多有用的结论或找出新的解题思路.让学生在解题过程中,不断进行信息的精致化和新信息的再探究,不断调节解题思路,从而使问题一步一步地得以解决. 图1 所以A′C=2AC,B′D=2BD, 所以Rt△A′CP∽Rt△B′DP, 所以∠CPA′=∠DPB′;B′,P,A′三点共线, 作OE⊥A′B′于点E, 因为A′B′为⊙O的弦,所以E为A′B′的中点, 设OE=d,0 设B′P为1份,则A′P为3份, 所以A′B′为4份,E为A′B′中点, 所以B′E为2份,从而PE为1份, 由0 即1 解法3利用椭圆可由圆均匀压缩而得到,利用圆和相似三角形的性质,根据线段的相似关系,将问题转化为利用m与圆心到圆的弦的距离d的关系,再由d的范围,求出m范围.解法3充分利用几何直观,借助视角化思维获得了新的解法,运算过程也大为简化. 以上三种解法,都有直觉观察和逻辑推理的互动互补,但都是正向思维,能否利用数形结合进行逆向思维,找到更出奇制胜的奇妙解法呢? 图2 由以上的证明,可将以上问题转化为如图2所示,在⊙O中,P是⊙O内异于圆心O的一定点,直线OP与⊙O交于两点M、N,A是⊙O上的点,那么A在何处时,PA取最值?如图2所示,在直线MN右侧,点A在圆上按顺时针运动到点A′,作直线l⊥PA,l交PA′于点C,在Rt△PAC中,PA 图3 也可以如图3所示,在直线MN右侧,点A在圆上按逆时针运动到点A′,作直线l垂直于半径OA,作PP′⊥l于点P′,显然PC 图4 亦可以如图4所示,设∠NPA=θ,0≤θ≤π,设OP=m,⊙O的半径为R,则m 在△POA中,由余弦定理得: R2=x2+m2-2mxcosθ, 显然,以x为自变量的函数是增函数.所以,当cosθ取最大值,即θ=0(点A在点N处)时,x最大,即PA最长;当cosθ取最小值,即θ=π(点A在点M处)时,x最小,即PA最短. 中学解析几何的内容主要涉及数式表征和图形表征,因此解题时,常要用到数形结合的思想.数形结合思想的具体应用中蕴涵着逻辑思维和直觉思维两种重要的思维方式,在解题过程中,图形与数式信息的相互作用不是一次就可以完成的,也不只是从图形信息到数式信息或者从数式信息到图形信息的单向流向,而是图形信息与数式信息的相互补充和交互作用. 在解题教学中,不要为解题而解题,把学生变成解题的机器.教师应通过引导学生对简单问题的深度思考,以问题为载体,把解题中蕴涵的数学思想方法和数学思维方式揭示出来,让学生在解题中学会思考,领悟数学的核心素养,掌握数学的思维方式.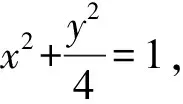
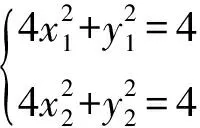
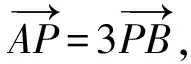

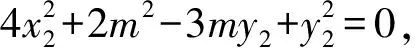
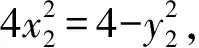
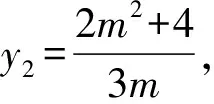
2 以形助数,另辟蹊径
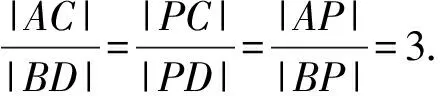

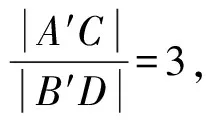
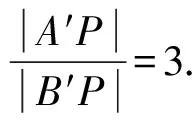
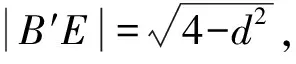
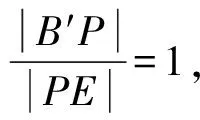
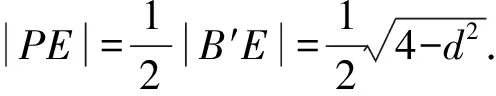
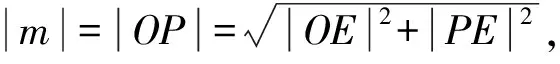
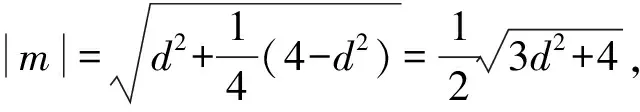
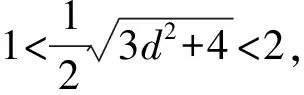
3 数形结合,出奇制胜