为有源头活水来—2018年高考数学全国III卷理科第16题探究

2018-11-16湖北省监利县实验高中433300万平方

中学数学研究(广东) 2018年19期

关键词：中点表现形式斜率

湖北省监利县实验高中(433300) 万平方

题目(2018年全国III卷理科第16题)已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点,若∠AMB=90°,则k=____.

此题取材平实,表现朴实,题干清晰,设问简洁,形式常见,但若对此题进行深入研究,细致品析,则会感觉它犹如一杯陈年老酒,浅尝平淡,深酌而显深厚蕴藉,余味绵长.

1.解法探究

本题有3个条件：

I.A,B在抛物线y2=4x上;

II.AB过焦点F(1,0);

III.∠AMB=90°.

条件I可有3种表现形式：①设四个参数A(x1,y1),B(x2,y2);②设两个参数利用抛物线的定义.

条件II可有4种表现形式：①AB在过焦点F的直线x=my+1上;②A,F,B三点共线;③利用抛物线的定义;④∠AFx=α.

结论可有3种表现形式：①直线形式x=my+1(或y=k(x-1));②斜率公式;③定义式k=tanα.

1.1 条件I采用设四个参数、条件II用AB在过焦点F的直线x=my+1上.

因为直线AB经过焦点F(1,0),且,故设其直线x=my+1,设AB与抛物线交点A(x1,y1),B(x2,y2)联立得.由根与系数的关系有y1+y2=4m,y1y2=-4.则

解法1因为∠AMB=90°,所以.则,所以.结论用直线形式,有.结论用斜率公式,有.

由此可知,直线方程设为x=my+1不是无意之举.如果条件III用斜率形式kMA·kMB=-1并结合(∗)可得：

解法2因为∠AMB=90°,所以kMA·kMB=-1.,即(y1-1)(y2-1)=0,下面同解法1.

评析解法1、2的核心思想是利用根与系数的关系进行整体代换,是解析几何解题的一种常规方法.

1.2 条件I采用设两个参数条件II采用A,F,B三点共线

解法3因为∠AMB=90°,所以,则利用(∗∗)有,所以a+b=1,从而k=2.

条件III用斜率形式kMA·kMB=-1与解法3类似,此处从略.利用条件III的几何意义1—两个直角三角形相似并利用 (∗∗)式有：

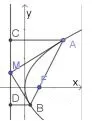
图1

解法4如图1,设A,B两点在准线x=-1上的射影分别为C,D,因为∠AMB=90°,所以Rt△ACM～Rt△MDB,则,而AC=AF=a2+1,BD=BF=b2+1,CM=2a-1,MD=1-2b,故,化简得,2(a+b)2-2(a+b)+1=0,所以a+b=1,从而k=2.

利用条件III的几何意义2—勾股定理并且利用(∗∗)式,便有：

解法5因为∠AMB=90°,所以|AB|2=|AM|2+|MB|2,则(a2+1)2+(2a-1)2+(b2+1)2+(2b-1)2=(a2-b2)2+4(a-b)2,化简得：(a+b)2-2(a+b)+1=0,所以a+b=1,从而k=2.

利用条件III的几何意义3—M在以为AB直径的圆上,并且利用 (∗∗)式,便有：

解法6因为∠AMB=90°,所以M在以为AB直径的圆上,而为AB直径的圆的方程为：(x-a2)(x-b2)+(y-2a)(y-2b)=0,则(-1-a2)(-1-b2)+(1-2a)(1-2b)=0,化简得：(a+b)2-2(a+b)+1=0,所以a+b=1,从而k=2.

评析从解法3至6可以清楚看到,条件I与II组合得到AB两点坐标的一个关系式ab=-1,条件III与II组合得到AB两点坐标的另一个关系式a+b=1,再用结论的斜率公式表现形式得到答案.整个解答过程就是寻找两个参数的积与和.从解答过程中可以看到AB中点的纵坐标为1与M的纵坐标相同.则可继续寻找新的组合.

1.3 条件I、II都采用用定义.

利用条件III的几何意义4—直角三角形斜边上的中线等于斜边的一半,便有：

图2

解法7如图2,设A,B两点在准线x=-1上的射影分别为C,D,E为AB的中点.因为∠AMB=90°,则 2ME=AB=AF+BF=AC+BD.由梯形中位线定理可知,ME为梯形ABDC的中位线,则M,E的纵坐标都为A,B纵坐标和的一半,即a+b=1.从而k=2.

利用条件III的几何意义5—直角三角形全等,便有：

解法8如图2,由解法7知,ME为梯形ABDC的中位线,从而ME=AE,∠AME=∠EAM,又∠AME=∠CAM,所以∠EAM=∠CAM,所以△ACM∼=△AFM,即MF⊥AB.而,从而k=2.

评析解法8可以看到平面几何在解析几何中的威力,直观想象核心素养体现得淋漓尽致,思路的得到缘于前面的铺垫,缘于抛物线定义的运用与平面几何性质的挖掘.

1.4 条件I采用用定义、条件II采用∠AFx=α.

解法9设∠AFx=α,则|FA|=|FA|cosα+p,所以.同理,把α换成π+α有：.

条件III采用向量形式与斜率形式都可得到：sinα=2cosα(过程略),从而k=tanα=2(结论的第3种表现形式).

说明解法9没有展开的原因是后面只是应用条件III的几种表现形式求值.

至此,我们可以看到,从审视题目条件入手,厘清条件的表现形式,再追踪到题目结论,明晰结论的呈现方式,然后将两者组合,进行对照分析,就能找到解决问题的方法.这样的方法不是“从帽子里变出一只兔子”,也不是解法的琐碎堆砌,这样的解法探究更不是无源之水,而是从题目出发的追本溯源,题目的条件和结论提供了解题思路的活水源头,对两者的表现形式进行多角度的有效性探究分析,可以完善知识系统的建构,有利于思维的训练.这样的解法探究着眼于知识要点,注重知识联系,从而拓展知识广度;这样的解法探究运用思想方法,拓展解题思路,凸显数学高度.

2.背景探究

2013年大纲卷理科第11题与本题几乎一模一样,可以说本题是13年题的重现.

题目(2013年大纲卷理科第11题)已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A,B两点,若,则k=()

本题有着丰富的高等几何背景,极点极线是高等几何的重要概念,本题中,点M(极点)对应的极线正好是AB,依据高等几何的结论：若抛物线y2=2px(p＞0),则点P(x0,y0)对应的极线方程为：y0y=p(x0+x).因此,AB的直线方程为1·y=2(-1+x),即y=2x-2,故k=2.此题可以“秒杀”!

从数学史的角度看,本题中的△MAB是阿基米德三角形.抛物线的弦与过弦的端点的两条切线所围的三角形称为阿基米德三角形.

有了这些背景认识,利用GeoGebra动态数学软件可以探究出阿基米德三角形的许多有趣性质.