基于L曲线与de Boor算法的正则化参数选取方法*
2018-05-29艾艺红
艾艺红, 邱 东
(1.重庆工商大学 派斯学院,重庆 401520;2.重庆邮电大学 理学院,重庆 400065)
函数微分方程的求解与运算一直以来都具有非常高的理论研究意义和应用价值[1-2].其中,作为微分方程中重要的研究内容,数值微分是一种利用离散点的函数值逼近该函数导数的方法,它被广泛应用于图像处理[3]、倒侦测系统[4]、管道建模与分析[5]等领域中.
现有数值微分方法主要包括两类:噪声知识方法[6-7],启发式方法[8-9].与噪声知识方法相比,启发式方法并不使用那些可用性较差的先验信息,而是基于正则化方法从问题和数据中提取这些信息,从而实现数值微分的准确运算[10].在现有研究中,蚁群优化[11]、L曲线[12]等都是比较成熟的方法,但这些方法在数值微分中的应用却很少.
在现有方法中,平滑样条曲线是一种应用非常广泛的数值微分方法.目前,已有很多学者研究了正则化参数选择问题,并给出了相关的研究成果.文献[13]对广义交叉验证法进行了优化,通过引入交替最小化算法提升了参数选取精度.文献[14]在传统广义交叉验证的基础上,提出了一种自适应参数获取方法,提高了算法的精度和鲁棒性.文献[15]提出了一种基于跟踪平衡差异原理的启发式方法,并借助样条工具箱执行相关仿真程序以验证所提方法在参数选取方面的优越性.
本文针对样条曲线中的正则化参数选择问题,提出一种参数选取方法:利用基于Hansen的正规化数据包的L曲线对函数进行平滑处理,采用de Boor算法对平滑处理后的函数进一步优化,进而借助正则化方法选择最优参数.基于Matlab仿真软件中的de Boor样条工具箱和正则化工具箱,验证了所提启发式算法在平滑曲线参数正则化选择中的有效性.
1 问题描述
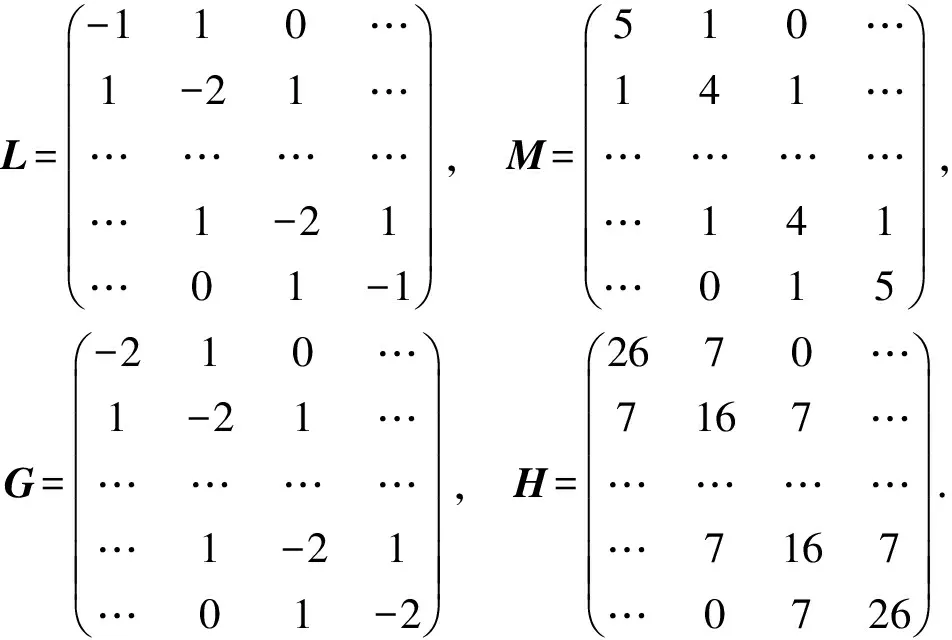
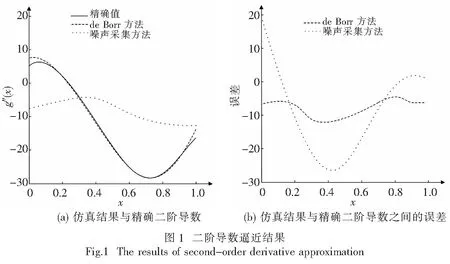
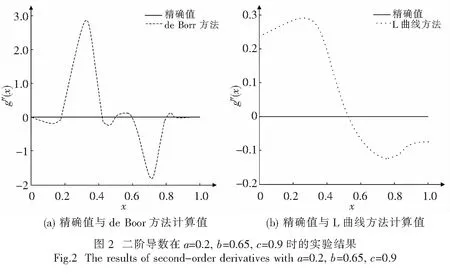
在给出解决方案之前,需要先对研究的问题进行简要叙述.假设y=y(x) 为[0,1]之间的函数,n为[0,1]之间的自然数,x0 |yi-y(xi)|≤θ, (1) 式中:i=1, …,n.所研究的问题即为基于测得的样本yi来构造函数的近似值及其特定阶次导数.该问题可描述为: (2) 式中:γ为正则化参数,当γ=0时,极小值为插值数据的曲线,当γ→∞时,极小值趋近于数据的最适合直线;g(x)∈Hk(0,1),g(0)=y0,g(1)=yn;Hk(0,1)的具体表达式可参见文献[15]. 当k=3时,问题(1)即对应了二阶导数的逼近问题.利用下式可以分段构造泛函的极小值: g(x)=αi+βi(x-xi)+χi(x-xi)2+δi(x-xi)3+εi(x-xi)4+φi(x-xi)5 . (3) 式中:xi=i/n.由式(3)可得相应的线性系统矩阵形式为: (4) 式中:d=1/n,α=(α1,α2,…, αn-1)T,χ= (χ1,χ2,…, χn-1)T,ε=(ε1,ε2,…,εn-1)T,y=(y1,y2,…,yn-1)T,z=(z1,z2,…,zn-1)T, 此时,(3)所示的k=3时问题可以转化为: min(qU1(gq)+(1-q)V1(gq)). (5) (6) q=1/(1+d4R(W1)/R(W2)),qR(·)=6(1-q)ATB2A. (7) 为了验证所提方法在数值微分参数选择中的优势,在Matlab中进行了仿真分析.仿真中,网格大小n=10,σ=δ2,U(g)=δ4.对于L曲线方法,使用文献[15]中的正则化工具箱,并对L曲线、广义交叉验证、de Boor等方法在选择正则化参数时的性能进行了对比分析. 实验中,选取d=1/n=0.1.在Matlab中的函数rand=(size(x))中增加噪声δ=3×10-2,得到rand=δ·(size(x)),用来模拟所提方法在提取数据时可以达到的精确程度,其中x为网格点向量.对比了de Boor方法和噪声采集方法的性能.实验结果如图1所示.由实验结果可知,与噪声采集方法相比,所提方法虽然没有利用与噪声相关的任何信息,但是却可以实现更好的跟踪性能,导数逼近误差几乎为零,而噪声采集方法则始终存在着较大的逼近误差. 为了验证所提方法在分段函数中参数选择的有效性,考虑以下函数: 对两种情况下的分段函数进行了仿真分析,包括:a=0.1,b=0.5,c=0.8和a=0.2,b=0.65,c=0.9.对分段函数来说,由于其具备明显的跳跃性,因此不仅具有一定的典型性,还可以充分说明所提方法在数值微分参数选择中的高精确性和强适应性.在实验中,通过近似一阶导数来检测函数的不连续点,噪声为δ=5×10-3的不连续点跳跃. 由图2可知,由于L曲线选择的q几乎等于1,其结果是渐近正态计算解,因此该方法并不利于不连续点的检测,在a=0.2,b=0.65,c=0.9的函数中,L曲线甚至会出现选择失败.相反,de Boor方法获得了非常好的实验结果. 针对离散函数导数逼近,采用光滑样条函数以及不连续性预测对参数进行正则化选取,在不依赖噪声测量的同时实现了参数的准确选择.通过将L曲线与de Boor方法进行有机整合,可以提高算法的精确度.在二阶导数逼近问题中进行了数值仿真实验,实验结果表明所提方法具有非常好的选取结果,甚至优于基于噪声的参数选取方法. 参考文献 [1] 郑志静, 王璐. 一种基于阶次转换的分数阶微分方程近似解法[J]. 湘潭大学自然科学学报, 2017, 39(4): 10-13. [2] 张强, 齐兴斌. 利用同伦摄动法的四阶微分方程数值解求解方法[J]. 湘潭大学自然科学学报, 2017, 39(2): 5-8. [3] ELLIOTT C M,SMITHEMAN S A. Numerical analysis of the TV regularization and H-1 fidelity model for decomposing an image into cartoon plus texture[J]. Communications on Pure & Applied Analysis, 2017, 6(4): 917-936. [4] WAGNER J,MAZUREK P,MORAWSKI R Z, et al. Regularized numerical differentiation of depth-sensor data in a fall detection system[C]//IEEE International Conference on Computational Intelligence & Virtual Environments for Measurement Systems & Applications, 2017: 234-236. [5] MAYSTRENKO A V,SVETLAKOV A A,GANDZHA T V, et al. Application of numerical signal differentiation methods to determine statio-narity of a process[J]. Petroleum & Coal, 2017, 59(3): 311-318. [6] SZOSTOK T. Functional inequalities involving numerical differentiation formulas of order two[C]//Bulletin of the Malaysian Mathematical Sciences Society, 2017: 1-14. [7] GAO W,ZHANG R. Multiquadric trigonometric spline quasi-interpolation for numerical differentiation of noisy data: a stochastic perspective[J]. Numerical Algorithms, 2017, 12(3): 1-17. [8] ALBANI V,CEZARO A D,ZUBELLI J P. On the choice of the Tikhonov regularization parameter and the discretization level: a discrepancy-based strategy[J]. Inverse Problems & Imaging, 2017, 10(1): 1-25. [9] ALJAMAL M F,ALOMARI A K,GOCKENBACH M S. Smoothing via elliptic operators with application to edge detection[J]. Inverse Problems in Science & Engineering, 2017,18(4): 1-20. [10] DAVYDOV O,SCHABACK R. Error bounds for kernel-based numerical differentiation[J]. Numerische Mathematik, 2016, 132(2): 243-269. [11] LAI M,TONG X. A metaheuristic method for vehicle routing problem based on improved ant colony optimization and Tabu search[J]. Journal of Industrial & Management Optimization, 2017, 8(2): 469-484. [13] ZHANG X,JAVIDI B,NG M K. Automatic regularization parameter selection by generalized cross-validation for total variational Poisson noise removal[J]. Appl Opt, 2017, 56(9): 35-47. [14] HUANG G, LI J, LUO C, et al. Regularization parameter adaptive acquisition based on improved GCV method and its application in pre-stack AVO inversion[C]//Seg Technical Program Expanded, 2017: 748-752. [15] FANG H,CHANG Y,ZHOU G, et al. Iteratively reweighted blind deconvolution with adaptive regularization parameter estimation[C]//IEEE Access, 2017,99: 1-1.2 新型正则化参数选择方法
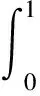
3 仿真分析
3.1 二阶导数近似实验
3.2 不连续性检测
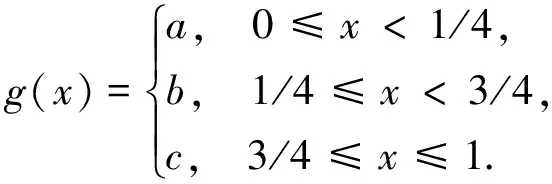
4 结 论

