冯志强,张云波

(山西大学 理论物理研究所,山西 太原 030006)

0 引言

一维量子气体大多是在光晶格里面制备的,例如:伊辛模型的仿真是在倾斜的晶格[1-2]中实现的,经典反铁磁性的研究是在三角晶格[3]中完成的,在极化的晶格气体[4-5]中可观测由自旋交换相互作用诱导而产生的偶极相互作用,短程反铁磁性是在二聚物晶格[6]中研究的。光晶格中的超冷原子气体为我们展示了丰富多彩的量子磁性,是凝聚态物理[7]研究的一个非常重要的领域。由于在光晶格中研究一维系统的局限性导致一些量子现象的缺失,例如:虽然短程反铁磁性在二聚物晶格[8]中已经被证实了,但由于经典光晶格实验具有很低的熵,导致实验上至今没有观测到光晶格中两组分费米气体的奈尔长程序。2014年德国汉诺威大学Deuretzbacher等[9]在理论上研究了谐振子势阱中强相互作用的一维旋量气体的量子磁性问题,同时提出了在谐振子势阱中冷原子系统实现有效自旋链的理论依据。同一时期Cui[10]也研究了在谐振子势阱中自旋轨道耦合对强相互作用的一维费米气体的影响。2015年德国Heidelberg大学Jochim小组[11]利用简谐势阱中囚禁的6Li原子在散射共振附近实现了反铁磁海森堡自旋链的精确制备,在无须外加光晶格的情况下对少数几个粒子的精确操控使得有效自旋链模型变为可能。这也为我们在冷原子中研究一维量子磁性开辟了另一条道路。

本文首先计算了在谐振子势阱和无限深方势阱中系统的能级排布和空间密度分布,然后利用有效自旋链模型计算了由不同粒子数构成的费米系统处于基态时各组分的自旋密度分布。最后通过在哈密顿量中引入一项与位置有关的磁场梯度,研究了磁场梯度对两组分的费米系统处于基态和激发态时自旋密度分布的影响。

1 有效自旋链模型

我们首先考虑一个由N个粒子(费米子或玻色子)组成的系统,这些粒子被外势所束缚(通常为谐振子势),粒子之间的相互作用通常可以等效成接触赝势(即δ相互作用),它可以通过实验测量并可利用费什巴赫共振(Feshbach Resonance)[12]来调节。其系统哈密顿量为:

(1)

其中M是粒子质量,g是粒子间相互作用强度,在散射共振附近即粒子间相互作用g很大但是有限值时,哈密顿量(1)可以约化为一个有效自旋链模型[9,13-14]:

(2)

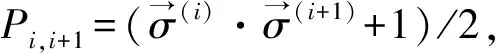
(3)

是相邻粒子之间的交换常数,θ(x1,…,xN)是阶跃函数,如果x1≤x2≤…≤xN那么θ(x1,…,xN)=1,否则等于0,我们将粒子从左到右依次标记。由于谐振子势阱的空间对称性,Ji=JN-i。ψF[15]表示由N个无相互作用费米子系统空间基态波函数,即Slater行列式。

现在我们利用有效自旋链模型计算一个由4个自旋1/2的费米子组成的系统的能级分布,这里我们用{N↑;N↓}表示N↑个自旋向上的粒子数和N↓个自旋向下的粒子数,系统总的粒子数满足N=N↑+N↓。对于{2;2}系统,在一维谐振子势阱中J1=J3≠J2,利用公式(3)计算得到J2/J1=1.312 62.通过求解该系统对应的薛定谔方程,可以得到其能谱:

(4)

(5)

(6)

(7)

(8)

E5=EF.

(9)

由于系统的哈密顿量(2)与总自旋S2对易,所以总自旋S是好量子数可以用来标记系统的本征能量。根据Lieb-Mattis定理[16]:对于自旋1/2的系统,当g>0时,系统的能量随着总自旋S的增加而增加,当g<0时系统的能量随着总自旋S的增加而减小。如图1(a)所示计算结果与定理保持一致。我们以EF作为零点能,用总自旋数S来标记系统的能量,可以看出强相互作用下系统不管处于基态还是激发态,能级都随着-1/g线性增加[17]。当-1/g<0,即Tonks气体区域,能量随着总自旋S的增加而增加;当-1/g>0,即Super-Tonks气体区域,能量是随着总自旋S的增加而减小。一维无限深方势阱是一个均匀的势阱,所以一维无限深方势阱中J1=J2=J3,用同样的方法可以计算出系统的能谱:

(10)

(11)

(12)

(13)

(14)

E5=EF.

(15)

如图1(b)所示在Tonks气体区域能量的变化趋势与在谐振子势阱中时一样都随总自旋S的增加而增加,在Super-Tonks气体区域随总自旋的增加而减小。由上述能谱公式表明在-1/g→0的附近能量是关于-1/g线性变化的。比较图1(a)和1(b)可以看出系统能量的排布不依赖与交换常数的比值J2/J1,而与系统总的自旋数S有关。现在我们以总自旋S=0所对应的两个能级为例来研究势阱的改变对能量的影响,当系统处于一维谐振子势阱时E0=5.072 66(-1/g),E1=3.962 76(-1/g).当系统处于一维无限深方势阱时E0=4.732 05(-1/g),E1=3.414 21(-1/g).一维谐振子势阱的能量E0,E1与无限深方势阱比较,能级关于-1/g的斜率分别偏移了0.340 61, 0.548 55.

Fig.1 Configuration of the energy spectrum of the system {2;2} in the harmonicoscillator potential well (a) and infinitely deep square potential well (b)，respectively图1 系统{2;2}处于谐振子势阱(a)和无限深方势阱(b)时的能级排布

2 两组分系统的自旋密度分布

实验上利用Stern-Gerlach可将不同自旋的原子气体分离,从而测量系统不同组分的密度分布,系统的第m组分的密度分布可以表示成下面的形式:

(16)

其中,m可以取自旋向上(↑)和自旋向下(↓)。这里

(17)

表示在坐标位置x处找到第i个粒子的概率,此时无须考虑第i个粒子的自旋。

(18)

表示第i个粒子处于任意一个自旋态上自旋磁性等于m的概率,其中χ表示由N个带有自旋的粒子组成的一个任意自旋态[9],它可以由系统的一组正交完备的基矢来表示。系统的空间密度分布等于系统中所有粒子的空间密度之和:

(19)

系统的空间密度分布的具体形式与系统所处的外势有关。首先在一维谐振子势阱中计算不同自旋粒子数组成的系统的密度分布,如图2所示,其中实线(ρhar)表示在谐振子势阱中系统的空间密度分布,图2(a)为3粒子系统,图2(b)为4粒子系统。然后我们将一维谐振子势阱换成一维无限深方势阱后继续研究了这两种系统的空间密度分布,虚线(ρsqu)表示在一维无限深方势阱中系统的空间密度分布。在一维无限深方势阱中我们选取的势阱边界是[-4,4],由于量子力学中波函数的有限性和连续性所以在无限深方势阱的边界上波函数等于零,即边界上粒子的概率为零。经过计算得出结论:系统空间密度分布会出现峰值,峰值的数量与粒子个数保持一致,例如:N=3则会出现3个峰值,N=4则会出现4个峰值。当系统处于一维谐振子势阱时,粒子密度分布呈现两边峰值低中间峰值高的空间对称分布形式;当系统处于一维无限深方势阱时,粒子密度分布呈现两边高中间低的空间对称分布形式。

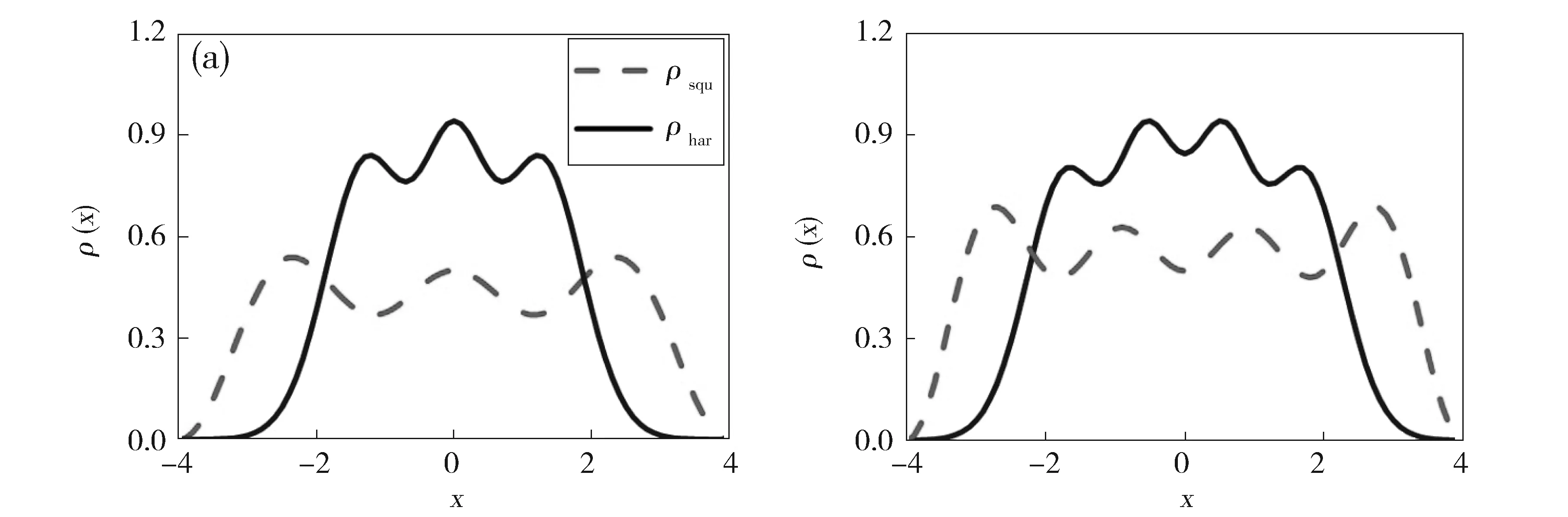
Fig.2 Spatial density distribution of the system for N=3 (a) and N=4 (b) in the harmonicoscillator potential well (solid lines) and infinitely deep square potential well (dashed lines), respectively图2 系统(N=3 (a)和N=4 (b))分别在一维谐振子势阱(实线)和无限深方势阱(虚线)中的空间密度分布

实验上可用散射共振的方法来[8]调节粒子间的相互作用,现在我们在原来的哈密顿量(2)后面加一项与位置有关的磁场梯度来继续讨论系统的自旋密度是如何发生变化的:

(20)

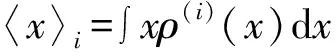
我们接着在一维无限深方势阱中继续计算了磁场梯度对系统{2;2}自旋密度的影响,计算结果显示当系统处于基态时,由于磁场梯度的影响自旋向上组分的密度分布也不再等于自旋向下组分的密度分布,而是两组分交替出现,呈现出反铁磁序[19]的排列方式如图4(a)所示, 可与图3(d)比较。当系统处于有些激发态时(第一激发态,第四激发态)系统的自旋分布会呈现出反铁磁排列,但处于另一些激发态时(第二,三,五激发态)则出现磁畴及更复杂的自旋密度分布。

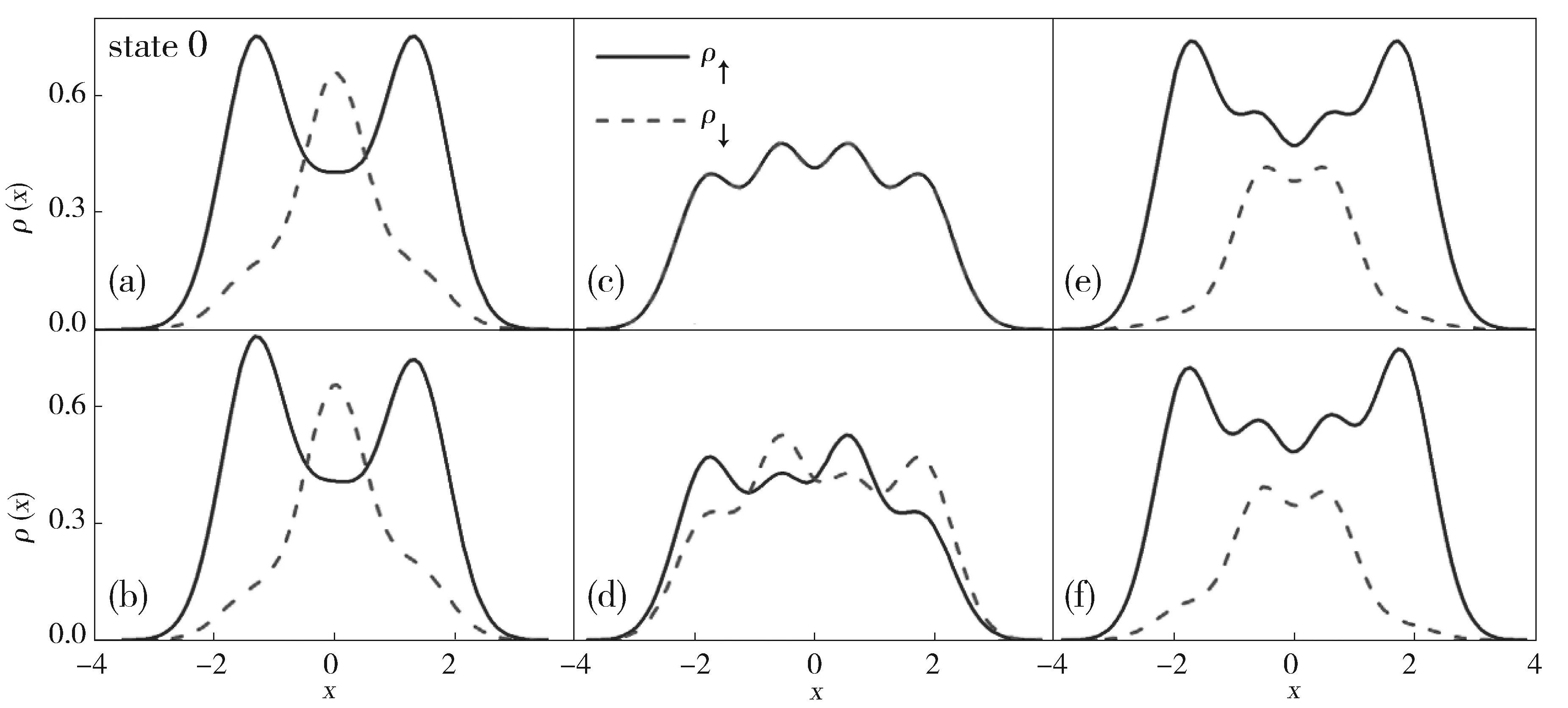
Fig.3 Spin density distribution without the B-field gradient at the ground state for the system( a{2;1},c{2；2},e{3;1}) in the harmonic oscillator potential well. The spin densitydistribution with the B-field gradient at the ground state for the system( b{2;1},d.{2;2},f{3;1} )图3 系统(a{2;1},c {2;2},e{3;1})在谐振子势阱中不加磁场梯度的自旋密度分布和系统(b{2;1},d{2;2},f{3;1})在谐振子势阱中加磁场梯度的自旋密度分布

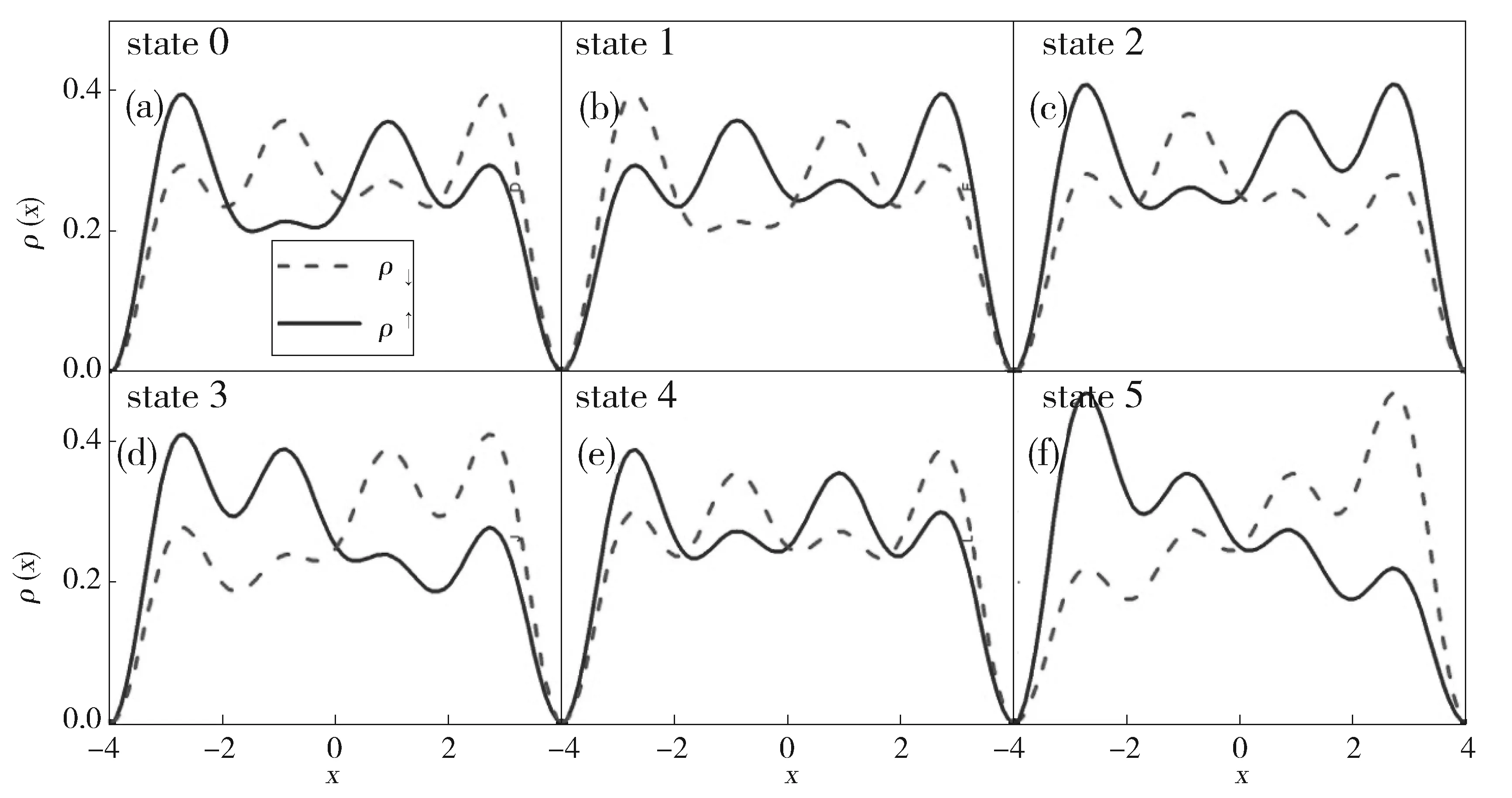
Fig.4 Spin density distribution of the two-components system with the B-field gradient respectivelyat the ground state, excited states in one-dimensional infinitely deep square potential well图4 在一维无限深方势阱中系统处于基态和各个激发态时，考虑上磁场梯度后两组分的密度分布

3 结论

有效自旋链模型为研究强相互作用一维量子气体提供了一种新颖的方法,本文主要利用此模型分别计算了在谐振子势阱和无限深方势阱中系统的能级排布和空间密度分布,结果表明系统能谱的排布和系统总的自旋数有关,而外势阱改变后能级会发生偏移。随着外势阱的改变系统的空间密度分布也出现了峰值位置的变化。随后在原先的哈密顿量的基础上引入了一项与位置有关的磁场梯度,我们分别在谐振子势阱和无限深方势阱中研究了磁场梯度对系统自旋密度分布的影响。计算结果显示这个磁场梯度能够改变系统的密度分布,自旋平衡的自旋链系统处于基态时,两组分自旋密度在空间会呈现出交替排布的反铁磁排序,对系统激发态的影响则出现磁畴及更加复杂的自旋密度分布现象。

参考文献：

[1] Simon J,Bakr W S,Ma R,etal.Quantum Simulation of Antiferromagnetic Spin Chains in an Optical Lattice[J].Nature,2011,472(7343):307-12.DOI:10.1038/nature09994.

[2] Meinert F,Mark M J,Kirilov E,etal.Quantum Quench in an Atomic One-Dimensional Ising Chain[J].PhysRevLett,2013,111(5):053003. DOI:10.1103/PhysRevLett.111.053003.

[3] Struck J,Ölschläger C,Le T R,etal.Quantum Simulation of Frustrated Classical Magnetism in Triangular Optical Lattices[J].Science,2011,333(6045):996-999.DOI:10.1126/science.1207239.

[4] Yan B,Moses S A,Gadway B,etal.Observation Of Dipolar Spin-Exchange Interactions with Lattice-Confined Polar Molecules[J].Nature(London),2013：501-521.DOI:10.1038/nature12483.

[5] Paz A,Sharma A,Chotia A,etal.Nonequilibrium Quantum Magnetism in a Dipolar Lattice Gas[J].PhysRevLett,2013,111(18):699-704.DOI:10.1103/PhysRevLett.111.185305.

[6] Greif D,Uehlinger T,Jotzu G,etal.Short-Range Quantum Magnetism of Ultracold Fermions in an Optical Lattice[J].Science,2013,340(6138):1307-10.DOI:10.1126/science.1236362.

[7] Auerbach A.Interacting Electrons and Quantum Magnetism[M].New York:Springer,2009.

[8] Zürn G,Serwane F,Lompe T,etal.Fermionization of Two Distinguishable Fermions[J].PhysRevLett,2013,108(7):075303.DOI:10.1103/PhysRevLett.108.075303.

[9] Deuretzbacher F,Becker D,Bjerlin J,etal.Quantum Magnetism without Lattices in Strongly Interacting One-Dimensional Spinor Gases[J].PhysRevA,2014,90(90):17590-17599.DOI:10.1103/PhysRevA.90.013611.

[10] Cui X L,Ho T L.Spin-Orbit-Coupled One-Dimensional Fermi Gases with Infinite Repulsion[J].PhysRevA,2014,89(1):432-435.DOI:10.1103/PhysRevA.89.013629.

[11] Murmann S,Deuretzbacher F,Zürn G,etal.Antiferromagnetic Heisenberg Spin Chain of a Few Cold Atoms in a One-Dimensional Trap[J].PhysRevLett,2015,115(21):215301.DOI:10.1103/PhysRevLett.115.215301.

[12] Cheng C,Grimm R,Julienne P.Feshbach Resonances in Ultracold Gases[J].RevModPhys,2010,82(2):63-85.DOI:10.1103/RevModPhys.82.1225.

[14] Gangardt D M,Shlyapnikov G V.Stability and Phase Coherence of Trapped 1D Bose Gases[J].PhysRevLett,2002,90(1):010401.DOI:10.1103/PhysRevLett.90.010401.

[15] Deuretzbacher F,Fredenhagen K,Becker D,etal.Exact Solution of Strongly Interacting Quasi One Dimensional Spinor Bose Gases[J].PhysRevLett,2008,100(16):77-82.DOI:10.1103/PhysRevLett.100.160405.

[16] Lieb E,Mattis D.Theory of Ferromagnetism and the Ordering of Electronic Energy Levels[J].PhysRev,2004,125(1):384-392.DOI:10.1103/PhysRev.125.164.

[17] Cui X L,Ho T L.Ground-State Ferromagnetic Transition in Strongly Repulsive One-Dimensional Fermi Gases[J].PhysRevA,2014,89(2):303-303.DOI:10.1103/PhysRevA.89.023611.

[18] Hao Y J.the Weakening of Fermionization of One Dimensional Spinor Bose Gases Induced by Spin-Exchange Interaction[J].EurPhysJD,2016,70(5):1-6.DOI:10.1140/epjd/e2016-70076-x.

[19] Hao Y J.Ground State Properties of Anti-Ferromagnetic Spinor Bose Gases in One Dimension[J].EurPhysJD,2017,71:47-6.DOI:10.1140/epjd/e2017-70483-5.