刘红彬，姜 乐，蒋宗彩

（1.河南财经政法大学 数学与信息科学学院，郑州 450046；2.郑州轻工业学院 数学与信息科学学院，郑州 450002）

0 引言

群决策在经济、管理中有着广泛的应用，群决策中的一个重要问题是选择合适的集结算子来集结决策者给出的判断信息。当前应用较多的算子如加权算术平均算子、有序加权平均算子、有序加权几何平均算子[1]等大多未考虑到数据之间的相互联系，这些算子中各数据的权重提前给定，或由某些函数计算得到。这些方法计算得到的权重与数据本身的大小或排序有关，与数据之间的接近程度无关。为了精确反映各集结数据之间的接近程度这一信息，Yager[2]提出了幂平均算子，该算子通过定义数据之间的支持函数，利用支持函数确定数据之间的权重，进而集结数据，该算子考虑了数据之间的相互联系，使过分大和过分小的数据的权重较小，在此基础上又介绍了幂加权平均算子、幂有序加权平均算子和幂广义平均算子。Xu和Yager[3]提出了幂几何算子、幂有序加权几何算子、不确定幂几何算子和不确定幂有序加权几何算子，研究了这些算子在群决策中的应用。Xu和Cai[4]提出了不确定幂加权平均算子和不确定幂有序加权平均算子，研究了基于这些算子的群决策方法。万树平[5]基于区间数幂平均算子研究了区间数多属性决策方法。

群决策中决策者评价信息常常以互补判断矩阵的形式给出，根据决策者对信息的掌握程度，互补判断矩阵的元素的常见形式有精确数、区间数、语言变量、区间语言变量等。由于客观事物的复杂性和人类思维的模糊性，有时决策者难以掌握足够的信息，三角模糊数互补判断矩阵也是一种常见的评价信息形式。与精确数和区间数相比，三角模糊数既可以体现决策者思维的模糊性，又可以反映决策者的某种确定性。关于三角模糊数互补判断矩阵的研究成果很丰富。徐泽水[6,7]研究了三角模糊数互补判断矩阵的排序方法。吴坚[8]提出了梯形模糊数互补判断矩阵的一种新的排序方法。黄卫来和黄松[9]，杨莉等[10]，侯福均和吴祈宗[11]，姜艳萍和樊治平[12]等对三角模糊数互补判断矩阵的排序问题都进行了研究。但以上成果在集结决策者判断信息时没有考虑到数据之间的相互联系。考虑到幂平均算子可以体现集结数据之间的接近程度，利用这一特点将其应用于群决策中个体意见的集结，可以体现群决策者意见的接近程度，使较大和较小的评价值具有较小的权重，从而集结结果具有较好的群体共识性，决策结果也更加可靠。为了将幂平均算子用于集结三角模糊数，本文提出三角模糊数幂平均算子和三角模糊数幂有序加权平均算子，并将提出的算子用于群决策，研究了基于三角模糊数互补判断矩阵的群决策方法，并进行实例验证。

1 预备知识

1.1 幂平均(PA)算子

定义1[1]：设PA:Rn→R,如果

其中a1,a2,…,an为待集结的一组数据，T(ai)=为支持函数，表示数据b对数据a的支持，满足：(1)Sup(a,b)∈[0,1],(2)Sup(a,b)=Sup(b,a),(3)如果，则Sup(a,b)≥Sup(x,y)，则称PA为幂平均算子。

PA算子也可以表示为：

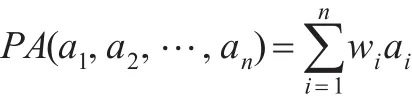
PA算子具有如下性质：

（2）有界性：

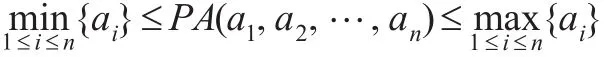
PA算子关于集结数据是非单调的，其原因是算子中的权重与数据大小有关，当某数据增加时，该数据的权重可能会变小，从而集结结果并非一定增加。

1.2 三角模糊数

以下给出三角模糊数的运算规则。

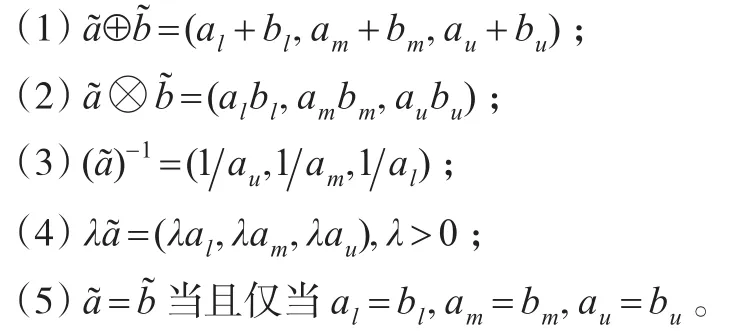
三角模糊数之间的距离有多种定义[13,14]，设=(al,am,au),=(bl,bm,bu)，本文采用文献[13]的定义方法，即，之间的距离：

关于三角模糊数的比较方法，目前研究成果很多[15-17],不同的方法对同一问题比较的结论往往不一致，目前还没有满意的有效方法。本文采用文献[17]中的方法。定义：

与其他方法相比，该方法比较三角模糊数得到的结果相对比较合理。特别在两个三角模糊数的左、右端点相同，中间端点不同时，该方法得到的结果比较合理，与人们的直觉相符。

定 义 3[7]：设 判 断 矩 阵=(ij)n×n，其 中ij=(alij,amij,auij),ji=(alji,amji,auji)，如果

2 三角模糊数幂平均(Tr-PA)算子

下面给出三角模糊数幂平均算子的定义，并研究其性质。

定义4：设Tr-PA:n→，其中表示三角模糊数集合，如果

下面讨论Tr-PA算子的性质。

定理1（有界性）：

证明：取定p≥1，计算出Dp(i,0),i=1,2,…,n，则1,2,…,n可 以 根 据Dp(i,0) 进 行 比 较 。 设，此处最大值的意义是按照本文中三角模糊数比较方法对1,2,…,n从大到小进行排序后，排在最大位置的三角模糊数，最小值的意义是类似的。由得：

证明：显然

所以结论成立。

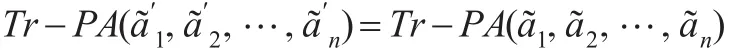
证明：由条件知

所以定理成立。

定理4：如果Sup(i,j)=0,i,j=1,2,…,n，则：

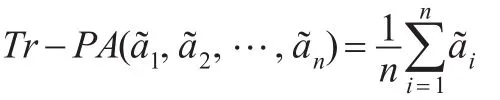
证明 ：由条件知，T(i)=0，i=1,2,…,n，所以，则结论成立。

注：类似于PA算子和UPA算子，Tr-PA算子关于被集结数据也是非单调的，即若i≥,i=1,2,…,n，并不一定有

3 三角模糊数幂有序加权平均(Tr-POWA)算子

定义5：设Tr-POWA:n→，如果

其中index(i)表示1,2,…,n中第i大的数据所对应的下标，→[0,1]为基本单位区间单调(BUM)函数，满足两个条件：(1)Q(0)=0,Q(1)=1,(2)如 果x＞y，则Q(x)≥Q(y)，则 称Tr-POWA为三角模糊数幂有序加权平均算子。

Tr-POWA算子与Tr-PA算子的区别在于集结前对数据按照从大到小的顺序进行了排列，数据的权重不仅与数据本身大小有关，还与数据所处的位置有关。Tr-POWA算子有以下几个性质：

定理5（有界性）：

定理8：如果Q(x)=x，则Tr-POWA算子即为Tr-PA算子。

所以定理成立。

注：类似于PA算子、UPA算子和Tr-PA算子，Tr-POWA算子关于被集结数据也是非单调的。

在Tr-PA算子和Tr-POWA算子中，支持函数起着十分重要的作用，在满足定义1中所述三个条件的前提下，类似于文献[2]中的方法，给出几种形式：

其中0≤d1＜d2＜…＜dp,0≤kp＜…＜k2＜k1≤1，p≥1。

设以下表达式中 0≤d(,)≤1，p,λ＞0，0≤k≤1：

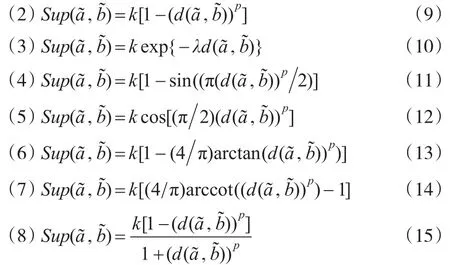
4 基于Tr-PA算子和Tr-POWA算子的群决策方法

首先给出群决策问题的描述。设X={x1,x2,…,xn}为备选方案集，决策者dk对备选方案两两比较，给出三角模糊数互补判断矩阵表示方案xi优于方案xj的程度，欲从中选择最佳方案。

本文中提出的Tr-PA算子和Tr-POWA算子可用于解决此类问题。若用Tr-PA算子，解决步骤如下：

步骤3：取定p≥1，利用式（4）定义的方法比较1,2,…,n的大小，选取偏好值最大的方案作为最佳方案。

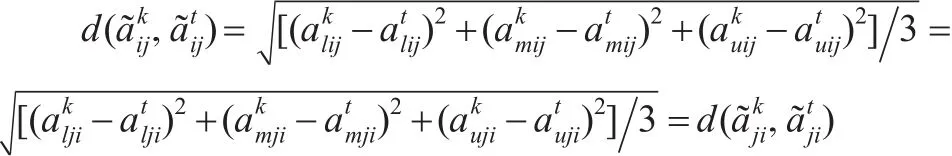
则：

即0≤alij≤amij≤auij≤1

若用Tr-POWA算子解决此问题，步骤如下：

（2）选择适当的 BUM 函数Q，设支持函数Sup(,)计 算 出，其中表示中第k大的三角模 糊 数 ，利用Tr-POWA算子集结决策者的判断，得到群判断矩阵，其中对任意。则显然矩阵仍为三角模糊数互补判断矩阵。

余下步骤与Tr-PA算子的步骤2和步骤3相同。

5 例子

设方案集为X={x1,x2,x3,x4}，三个决策者d1,d2，d3对方案进行两两比较，给出三角模糊数互补判断矩阵为（文献[12]）：

首先利用Tr-PA算子解决此问题。

（3）设p=1 ，比较的大小，可得，从而最佳方案为x4。

下面再用Tr-POWA算子分析此问题。在式（4）中取p=2，取BUM函数Q(x)=，按照前文所述步骤得则，最佳方案为x1。该结果与利用Tr-PA算子不同，主要原因在于该方法中的数据权重同时与数据本身和BUM函数有关，即除了与数据有关以外，还与数据在排序中所处的位置有关。

文献[12]中的结果是x1≻x4≻x3≻x2，与本文中使用Tr-PA算子得到的结论不同。主要原因是文献[12]未考虑数据之间的相互联系，本文中利用Tr-PA算子集结数据的过程中，考虑到了数据之间的接近程度，体现了数据之间的细微差别和联系，使大小比较接近的数据具有较大的权重，而在这些比较接近的数据中，数据的权重又与数据的大小成正比，过大和过小的数据权重较小。使过大和过小的数据对集结结果的影响降低，同时，中间数据对集结结果的影响增加，特别是其中较大数据的影响比较大，集结结果比较符合人们的思维习惯。Tr-POWA算子也考虑了数据之间的关系，同时考虑了数据在排序中的位置。通过选取不同的BUM函数，排在同一位置数据的权重会有所不同，增加了决策者的灵活性。定理8表明Tr-PA算子是Tr-POWA算子的一种特殊情形，从而Tr-POWA算子具有更强的适用性，得到的决策结果也更加合理。

6 结束语

本文在精确数的PA算子和区间数的UPA算子的基础上提出了三角模糊数Tr-PA算子和Tr-POWA算子。如果决策者的判断信息以三角模糊数互补判断矩阵的形式给出，利用这两种算子集结数据，可以体现数据之间的相互联系，充分利用数据中所包含的信息。计算实例表明，本文中所提出的决策方法是可行的。

[1]Xu Z S,Da Q L.An Overview of Operators for Aggregating Information[J].International Journal of Intelligent Systems,2003,18(9).

[2]Yager R R.The Power Average Operator[J].IEEE Transactions on Systems,Man,and Cybernetics,Part A,2001,31(6).

[3]Xu Z S,Yager R R.Power-Geometric Operators and Their Use in Group Decision Making[J].IEEE Transactions on Fuzzy Systems,2010,18(1).

[4]Xu Z S,Cai X Q.Uncertain Power Average Operator for Aggregating Interval Fuzzy Preference Relations[J].Group Decision and Negotiation,2010,21(3).

[5]万树平.基于幂均算子的区间型多属性决策方法[J].控制与决策,2009,24(11).

[6]徐泽水.三角模糊数互补判断矩阵排序方法研究[J].系统工程学报，2004,19(1).

[7]徐泽水.基于FOWA算子的三角模糊数互补判断矩阵排序方法[J].系统工程理论与实践,2003,23(10).

[8]吴坚.一种新的梯形模糊数互补判断矩阵的排序方法[J].中国管理科学,2010,18(3).

[9]黄卫来，黄松.一种改进的三角模糊数互补判断矩阵的排序方法[J].系统工程与电子技术,2007,29(7).

[10]杨莉，李南，和媛媛.三角模糊数互补判断矩阵的加性一致性及排序[J].系统工程,2009,(3).

[11]侯福均，吴祈宗.I型不确定数互补判断矩阵的一致性和排序研究[J].系统工程理论与实践,2005,25(10).

[12]姜艳萍，樊治平.三角模糊数互补判断矩阵排序的一种实用方法[J].系统工程,2002,20(2).

[13]Chen C T.Extensions of the TOPSIS for Group Decision Making Under Fuzzy Environment[J].Fuzzy Sets and Systems,2000,114(1).

[14]Zwick R,Carlstein E,Budescu D V.Measures of Similarity Among Fuzzy Concepts:A Comparative Analysis[J].International Journal of Approximate Reasoning,1987,1(2).

[15]Facchinetti G,Ricci R G,Muzzioli S.Note on Ranking Fuzzy Triangular Numbers[J].International Journal of Intelligent Systems,1998,13(7).

[16]Cheng C H.A New Approach for Ranking Fuzzy Numbers by Distance Method[J].Fuzzy Sets&Systems,1998,95(3).

[17]Abbasbandy S,Asady B.Ranking of Fuzzy Numbers by Sign Distance[J].Information Sciences,2006,176(16).