孙冠华

（南京大学 商学院，南京 210093）

1 问题的提出

时间序列分析是处理以时间为指标集的随机变量序列{xt:t∈T}的理论。指标集T可以是区间，如[0, ∞)；也可以是离散数集，如N+，对应的时间序列分别称为连续时间序列和离散时间序列。时间序列分析理论内容丰富，包括数据描述性统计、模型的定阶、参数的估计和检验以及分析和预测等。研究时间序列有各种各样的目的，包括对数据生成机制的理解和描述、对未来值的预报，以及对系统的最优化控制等。时间序列的本质特征主要表现为：观察值之间是相互依赖的或相关的，以及观察值是有序的。因此，建立在独立性假设基础之上的统计技术和方法不再适用，需要建立不同的统计方法。

作为数理统计学的一个组成部分，时间序列分析的发展和主流统计学理论的发展有很大的一致性。20世纪上半叶，伴随着多元线性回归模型的广泛应用，一批时间序列模型包括自回归模型、移动平均模型以及移动平均自回归模型相继建立起来。近年来，随着科学技术的发展以及人类实践活动范围的扩大，非线性理论受到广泛关注。以核方法为代表，统计学中出现了一系列的非线性回归分析技术。同时，在时间序列领域，以bilinear模型为代表的非线性时间序列模型随之建立并得到广泛应用，Tong（1990）提供了一个很好的介绍。

金融时间序列分析是时间序列分析理论中较为活跃的一个分支。20世纪70年代以来，伴随着科技的进步、计算机的普及，金融交易成本和准入门槛均有较大的降低，这为金融市场的活跃提供了有利条件。在参与积极性提高的同时，出于对超额收益的追求，人们普遍希望建立准确预测金融市场的模型，因而ARCH、GARCH等波动模型相继出现，极大促进了金融时间序列理论的研究。然而，21世纪初，一场由次级按揭贷款引发的全球金融危机席卷全球金融市场，大量金融机构破产、工人失业，冷酷的现实提醒着人们：理论界对金融市场的认识与真正的金融市场之间还有很大距离。

总体而言，对时间序列的建模分析可以归结为寻找合适的多元函数f(⋅)，使得下式成立：

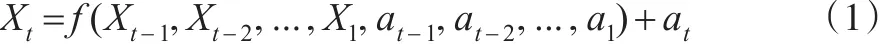
这里X1,X2,...,Xt-1为往期观察值，a1,a2,...,at为随机误差，二者间相互独立，且a在X给定条件下服从正态分布。根据函数f(⋅)性质不同，可将时间序列分为两类：当函数f(⋅)为线性函数时，该时间序列为线性时间序列；当函数f(⋅)为非线性函数时，该时间序列为非线性时间序列。

2 实验设计

本文设计两个实验，用对比的方式来说明ARMA模型与bilinear模型在数值拟合方面所具有的不同特性。

为了能更好地显现结论的对比性，本文选择使用比较简洁的模型进行模拟。并且，为了不致于使实验过程更加繁琐，此处暂不考虑定阶问题。采取以下两个模型：

一阶ARMA模型rt=φ0+φ1rt-1+θ1at-1+at

bilinear模型rt=φ0+φ1rt-1+θ1at-1+η11rt-1at-1+at

可以看到，两者最大的不同在于bilinear模型中引进的非线性项η11rt-1at-1。该项的引入会使模型的估计出现两方面变化：一方面，参数的增加往往会使计量模型估计的精度有所增加，经典线性模型尤其如此。另一方面，由于样本的有限性，参数的估计存在误差，增加的参数会将误差引入模型，使得模型的精确度降低。引入参数最终给模型精确度带来的变化取决于两种力量的对比。

为了比较两个模型在数据拟合方面的精确性，本文进行如下实验：首先，用如上的ARMA模型产生数据，然后分别用系数未知的ARMA模型与bilinear模型进行拟合，考察两个模型拟合的残差并进行比较。随后再用bilinear模型产生数据，并用同样的方式进行拟合，分别得到另一组残差序列。将两组残差序列进行比较，若某一组残差明显小于另一组，则说明对应的模型在数值拟合方面具有优势，否则，说明两个模型拟合数据能力相当。

本文选取的数据产生模型为：

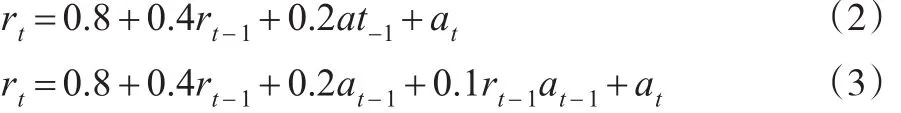
考虑到单次实验的不确定性，本文采用重复实验进行模拟。实验设计如下：共分两组进行，第一组用模型（2）产生收益率序列，分别用含有未知参数的ARMA模型和bilinear模型进行数据拟合，求解未知参数并计算得到的残差值。将此实验分别重复500次和1000次，计算残差序列均值、标准差。第二组改用模型（3）产生收益率序列，其他设置相同。两组实验的误差均值和标准差分别见表1和表2所示。

表1 重复次数为500次时误差结果对照表

表2 重复次数为1000时误差结果对照表

在表1和表2中，行用来表示原始数据模型，列用来表示拟合模型。如表1第二行表示数据是用ARMA模型产生的，而第二列表示用ARMA模型拟合，交叉处的0.7553（0.9404）表示实验重复500次时，由ARMA模型产生的数据用ARMA模型拟合误差均值为0.7553，标准差为0.9404。

从实验一中可以看到，当原始数据是由ARMA模型产生，即数据结构为线性时，用bilinear模型与ARMA模型拟合准确度相近，分别只相差0.29和0.23个百分点。而当原始数据是由bilinear模型产生，即带有非线性结构时，用bilinear模型具有较明显的优势，精度比ARMA模型分别提高了1.91和1.92个百分点。这说明作为ARMA模型的扩展，bilinear模型无论在处理线性或是非线性模型方面都有较好的表现，并没有产生参数增加引起误差增大的问题。

在上述实验中，可以看到对于带有非线性结构数据的拟合，bilinear模型要优于ARMA模型。一个比较自然的问题是：是否随着数据序列中非线性成分的逐渐增加，bilinear模型在数据拟合上的优势会逐渐增加？这是一个值得研究的问题，本文设计第二个实验如下：

将数据产生模型（3）中非线性项rt-1at-1前系数由0.1顺次增加到1。对每个确定的系数值，分别重复上述实验，按同样的方式比较所得结果如表3所示。

表3 不同程度非线性条件下两模型拟合误差对照表

可以看到，随着非线性项系数的增加，bilinear模型的估计效果仍然较好，而ARMA模型的误差增长较快，更加直观的对比可见图1所示。可以认为，在非线性结构较为显著的数据下，ARMA模型几乎失效。

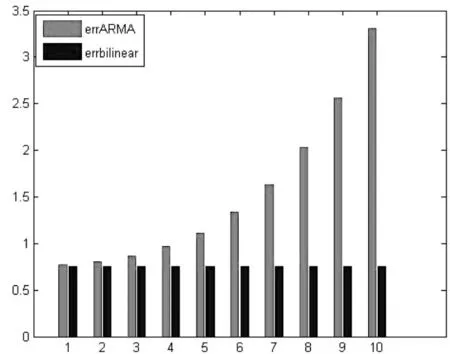
图1 非线性部分占比增加时两模型误差比较

3 结论

本文从数值拟合这一特定视角，选取了线性模型和非线性模型的各自代表——ARMA模型和bilinear模型进行分析，得到了如下结论：（1）对于线性数据，两模型拟合程度相近，而对于具有非线性结构的数据，bilinear模型拟合准确度优于ARMA模型。（2）原始数据中非线性结构所占比重越大，bilinear模型在拟合方面的优势越明显。鉴于bilinear模型可以认为是ARMA模型的非线性扩展，这个结果是符合直觉的。

在模型选择问题中，模型的准确性并不必然随着参数数目的增加而提高。如著名的三因子模型，仅用三个因子就可以解释股价收益率变化的90%，提高空间十分有限。但在本文中，交叉项的引入确实使得模型的拟合精度有所增加。说明模型的选择并不能遵循公理性法则，而应具体问题具体分析，灵活取舍。

为了更加简洁明了地体现模型差异，本文并没有考虑模型定阶问题，而是预先选定了模型滞后阶数。一个自然的问题是当滞后阶数没有事先给定时是否还有类似结论成立，可以继续就此问题进行研究。另外，bilinear模型是通过ARMA模型引入交叉项得到的，可以认为是式（1）中函数f(⋅)进行泰勒展开至二阶的结果，比只展开到一阶的ARMA模型更准确是合理的。是否可以沿此方向研究更高阶的模型？这样的模型是否有比bilinear模型更加有效的拟合性质？仍然是值得考虑的问题。

[1]Bollerslev T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometics,1986,(31).

[2]Engle R F.Autoregressive Conditional Heteroscedasticity With Estimates of Variance of United Kindom Inflations[J].Econnometrica,1982,50(4).

[3]Tsay R S.Time Series and Forecasting:Brief History and Future Research[J].Journal of the American Statistical Association,2000,95(450).

[4]Yule G U.On a Method of Investigating Periodicities in Disturbed Series,With Special Reference to Wolfer’s Sunspot Number[J].Philosophical Transactions of the Royal Society B Biological Sciences,1927,(226).

[5]Box G,Jenkins G,Reinsel G.Time Series Analysis:Forecasting and Control[M].Englewood Cliffs,N.J.:Prentice Hall,1994.

[6]Granger C W J,Anderson A P.An Introduction to Bilinear Time Series Models[M].Gottingen:Vandenhoek and Ruprecht,1978.

[7]Härdle W.Applied Nonparametric Regression[M].Cambridge:Cambridge University Press,1990.

[8]Rao T S,Gabr M M.An Introduction to Bispectral Analysis and Bilinear Time Series Models[M].New York:Springer Verlag,1984.

[9]Tsay R S.Analysis of Financial Time Series[M].New Jersey:John Wiley&Sons,2010.

[10]Tong H.Threshold Models[M].New York:Springer,1983.

[11]Tong H.Non-linear Series:A Dynamical System Approach[M].Oxford:Oxford University Press,1990.

[12]魏武雄.时间序列分析：单变量和多变量方法[M].北京：中国人民大学出版社，2009.