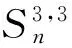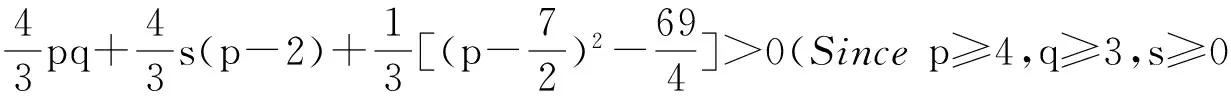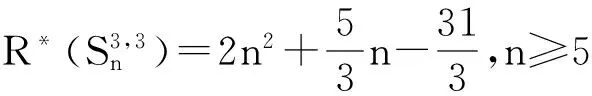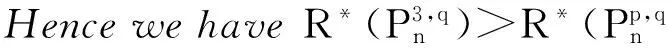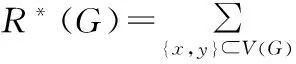Bicyclic Graphs with Extremal Multiplicative Degree-Kirchhoff Index
2017-06-28,,,
, , ,
(College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China)
Bicyclic Graphs with Extremal Multiplicative Degree-Kirchhoff Index
ZhuZhongxun,HongYunchao*,LuoAmu,WangWeifeng
(College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China)

distance;multiplicativedegree-Kirchhoffindex;bicyclicgraphs
LetG=(V(G),E(G))beaconnectedsimplegraph.ThedistancedG(x,y)isdefinedasthelengthofashortestpathbetweenverticesxandyinG.SupposethatG1andG2aretwodisjointconnectedgraphswithu1∈V(G1)andu2∈V(G2),let(G1,u1)⊕(G2,u2)bethegraphcreatedbycoalescenceofverticesu1andu2.AgraphGiscalledbicyclicgraphif|E(G)|=|V(G)|+1[1,2].
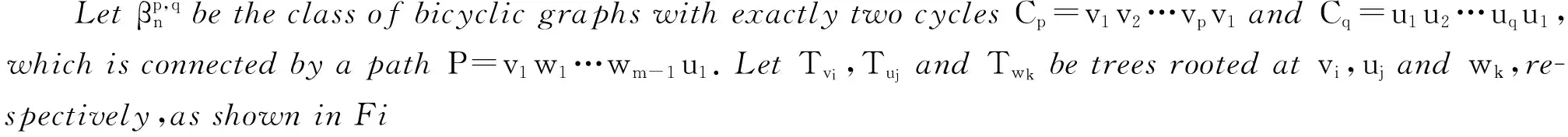
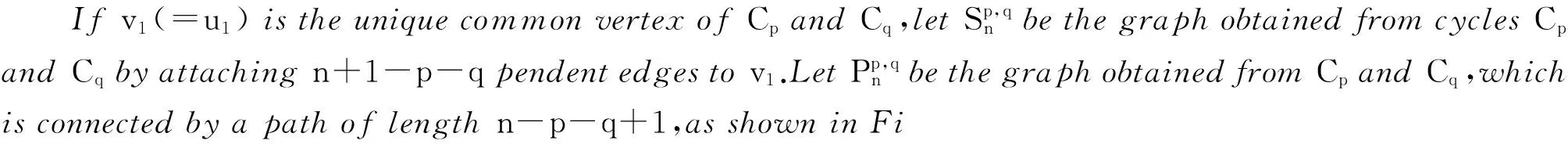


Fig.图1 图
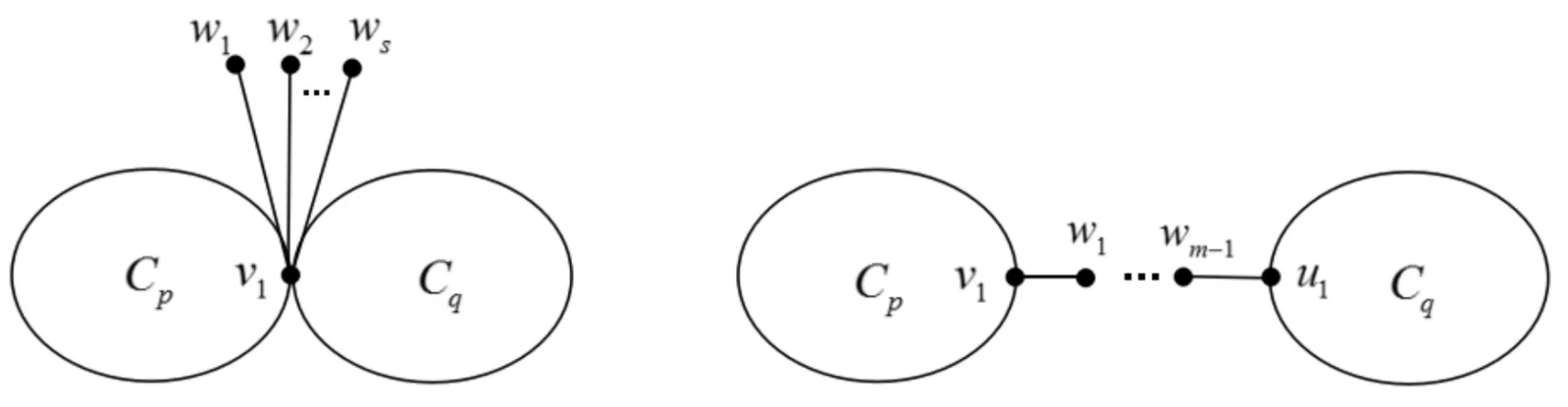
Fig.图2 图和

The following lemmas that will be used in the proof of our main results.
Lemma 1[4]Letube a cut vertex of a connected graphG,xandybe two vertices in different components ofG-u,thenrG(x,y)=rG(x,u)+rG(u,y).
Lemma 2[7,8]LetPn,CnandSnbe the path,the cycle and the star onnvertices,respectively. Then
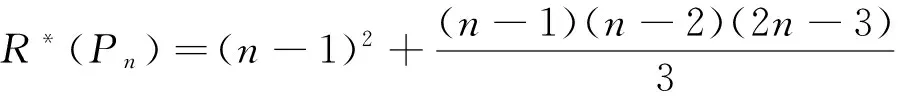
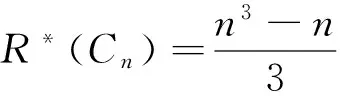
R*(Sn)=(n-1)(2n-3).
Lemma 3[7,8]LetG1andG2be connected graphs with disjoint vertex sets,withm1andm2edges,respectively. Letu1∈V(G1) andu2∈V(G2). Constructing the graphGby identifying the verticesu1andu2,and denote the so obtained vertex byu. Then
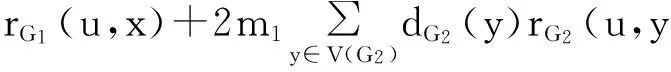
1 Some Transformations
Inthissection,wewillgivesometransformationswhichwilldecreaseorincreaseR*(G).
Transformation1Letu1u2beacut-edgeofbicyclicgraphG,Cp,CqbetheconnectedcomponentsofG-u1u2,whereu1∈V(Cp),u2∈V(Cq) .
ConstructingthegraphG*fromGbydeletingu1u2andidentifyingtheverticesu1,u2,denotethesoobtainedvertexbyu,addinganpendentedgeuv.
Lemma4LetG,G*bethegraphsdescribedinTransformation1,thenR*(G)>R*(G*).
ProofLet|V(Cp)|=p,|V(Cq)|=q,and|E(Cp)|=p,|E(Cq)|=q.LetH=G[V(G)(V(Cq)-u2)],H*=G[V(G*)(V(Cq)-u)].
ByLemma3,wehave:

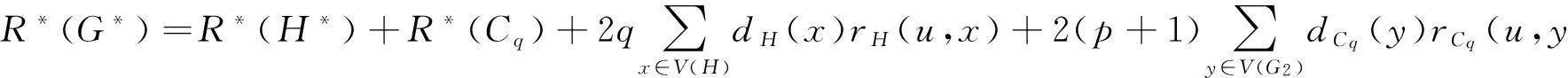
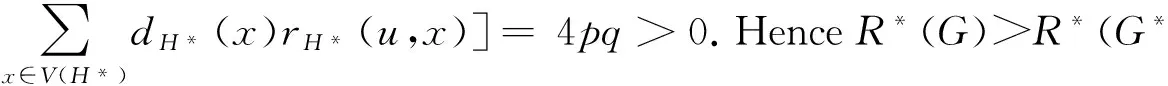
Letβnbe the class of connected graphs onnvertices. By Transformation 1 and Lemma 4,we have the following result.
Corollary 1 LetG0be a graph with the smallest multiplicative degree-Kirchhoff index inβn,then all cut-edges are pendent edges.
Transformation 2 LetGbe a bicyclic graph withV(G)={u,v,v1,v2,…,vs}∪V(Cp)∪V(Cq),for whichvis a vertex of degrees+1 such thatvv1,vv2,…,vvsare pendent edges incident withv,anduis the neighbor ofvdistinct fromvithat is on the cycleCq. The other cycleCponly has one common vertexwwithCq. We form a graphG′=σ(G,v) by deleting the edgesvv1,vv2,…,vvsand adding new edgesuv1,uv2,…,uvs. We say thatG′ is aσ-transform of the graphG.
Lemma 5 LetGandG′ be the graphs defined in Transformation 2. ThenR*(G)>R*(G′).
Proof LetT=G[{v,v1,v2,…,vs}],H=G[V(G)V(T)],then
dG(u)dG(v)rG(u,v).
dG′(u)dG′(v)rG′(u,v).
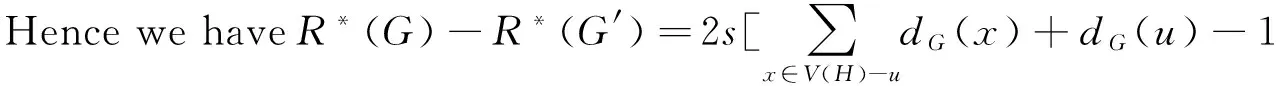
Lemma 6 LetG0be a bicyclic graphGwithV(G)={v1,v2,…,vs}∪V(Cp)∪V(Cq),for whichuis a vertex of degrees+2 in the cycleCqof the bicyclic graphG0,anduv1,uv2,…,uvsare pendent edges incident withu,and the other cycleCponly has one common vertexwwithCq. Let graphG1delete the edgesuv1,uv2,…,uvs,and add new edgeswv1,wv2,…,wvs. ThenR*(G0)>R*(G1).
Proof LetG=G0[V(Cp)∪V(Cq)],H0=G[V(G0)(V(G)-u)],andH1=G[V(G1)(V(G)-w)],thenH0≅H1≅K1,s. By Lemma 3,we have:

R*(G1)=R*(G)+R*(K1,s)+
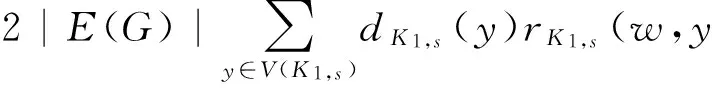
Hence we get:
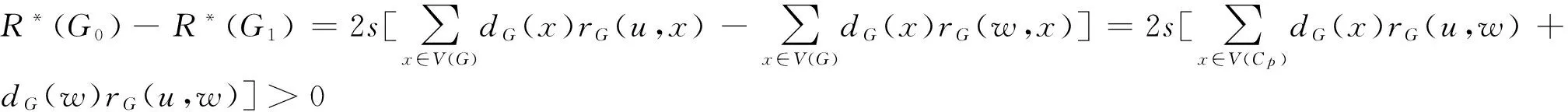
Then we haveR*(G0)>R*(G1).
Transformation 3 LetGbe a bicyclic graph withV(G)={u,v,v1,v2,…,vs}∪V(Cp)∪V(Cq),for whichvis a vertex of degrees+1 such thatvv1,vv2,…,vvsare pendent edges incident withv,anduis the neighbor ofvdistinct fromvithat is on the cycleCq. The other cycleCponly has one common vertexwwithCq. We form a graphG″=π(G,v) by deleting the edgesvv1,vv2,…,vvsand connectingviand all the isolated vertices into a pathvv1v2…vs.
We say thatG″ is aπ-transform of the graphG.
Lemma 7 LetGandG″ be the graphs defined in Transformation 3. ThenR*(G) Proof LetT=G[{v,v1,v2,…,vs}],H=G[V(G)V(T)],R*(G) is defined in Lemma5,then dG″(u)dG″(v)rG″(u,v). Hence we have: Lemma 8 LetG0be a bicyclic graph with the vertex setV(Cp)∪V(Cq)∪V(Ps+1), in whichV(Cp)∩V(Ps+1)={v} andV(Cq)∩V(Ps+1)={w}. Forwa∈E(Ps+1), andu∈V(Cq), letG1=(G0-{aw})∪{ua},thenR*(G0)>R*(G1). Proof LetH,H0andH1be the graphs as shown in Fig.3,then we have G0=(H,vs-1)⊕(H0,a), G1=(H,vs-1)⊕(H1,w). By Lemma 3,we have: R*(G0)=R*(H)+R*(H0)+2(q+1)· R*(G1)=R*(H)+R*(H1)+2(q+1)· HenceR*(G0)-R*(G1)=4(p+s-1)[q-rCq(w,u)]≥0. Ifq=rCq(w,u),thenwanducoincidence,G0andG1is isomorphic. SinceG0andG1is not isomorphic,therefore we getR*(G0)-R*(G1)>0. This completes the proof. Fig.3 Graphs H,H0 and H1图3 图H,H0和H1 In this section,we will characterizen-vertex bicyclic graphs with exactly two cycles having the minimum and maximum multiplicative degree-Kirchhoff index. (1) In Fig.1,Tvi,TujandTwkare all stars with their centers atvi,ujandwkfor eachi,jandk. Without loss of generality,suppose that treeTviis not a star. LetG1be constructed fromG0by deleting all the edges ofTviand connecting all the isolated vertices tovi. By Lemma 5,we haveR*(G0)>R*(G1),which contradicts the choice ofG0. Hence (1) holds. (2) The length of the path connects the two cycles inG0is zero. Suppose that there exist the length of path isk(k≥1) inG0. Assume thatv1=w0,u1=wk. Lete=wiwi+1be an edge of path. LetG2be the graph obtained fromG0by first contractingeand then attaching a pendent edgewiatowi. Assume thatG01andG02are two components ofG0-eandG21andG22are copies ofG01andG02inG2,respectively. See Fig.4. Fig.4 Graphs G0 and G2图4 图G0和G2 By Lemma 4 and Corollary 1,we haveR*(G0)>R*(G2). This contradicts the hypothesis. Hence (2) holds. (3) In Fig.1,ifp+q≤n,then onlyTv1(Tv1=Tu1) is nontrivial. Without loss of generality,suppose to the contrary that treeTui(i≠1) is nontrivial. By Lemma 6,we getR*(G0)>R*(G1), which contradicts the choice ofG0. Hence (3) holds . According to (1)-(3),we get Theorem 1 . (1) In Fig.1,Tvi,TujandTwkare all paths with their centers atvi,ujandwkfor eachi,jandk. Without loss of generality,suppose that treeTviis not a path. LetG1be constructed fromG0by deleting all the edges ofTviand connecting all the isolated vertices into a path. By Lemma 7,we haveR*(G1)>R*(G0),which contradicts the choice ofG0. Hence (1) holds. (2) Assume thatTw0=Tv1andTwm=Tu1,thenTwiis trivial 0≤i≤m). If not,without loss of generality,suppose that there is nontrivialTwj. By (1),we know thatTwjis a path withwjas its end vertex and assume thatuis the other end vertex. LetG2=G0-wjwj+1+uwj+1(ifj=m,G2=G0-wj-1wj+uwj-1). Assume thatG01andG02are two components ofG0-wjwj+1andG21andG22are two components ofG2-uwj+1. See Fig.5. In the following,we proveR*(G2)>R*(G0). LetH0=G02+wjwj+1,H2=G22+uwj+1,rG(wj,u)=s, then by Lemma 3,we get: Ifs=0,thenG0andG2isisomorphic.SinceG0andG2isnon-isomorphic.ThereforeweobtainR*(G2)>R*(G0). Thiscontradictsthehypothesis.Hence(2)holds. (3)InFig.1,ifp+q≤n,thenTviandTujaretrivialforeachiandj. Fig.5 Graphs G0 and G2 图5 图G0和G2 Without loss of generality,suppose to the contrary that treeTvi(i≠1) is nontrivial. By Lemma 8,we getR*(G0)>R*(G1), which contradicts the choice ofG0. Hence (3) holds. According to (1)-(3),we get Theorem 2. Proof Letu1,u2,wbe three successive vertices lying on theCpof the bicyclic graphG1. The other cycleCqonly has one common vertexwwithCp. Andwv1,wv2,…,wvsare pendent edges incident withw. Let the graphG2is obtained by deleting the edgesu1u2and adding the edgewu2. ThenR*(G2)< R*(G1). LetH1=G[V(G1)(V(Cq)-w)],H2=G[V(G2)(V(Cq)-w)],then ProofLetu1,w,u2bethreesuccessiveverticeslyingontheCpofthebicyclicgraphG3.ThecycleCpandCqarelinkedwithtwoendverticesvandwofPs+1.LetthegraphG4isobtainedbydeletingtheedgewu2andaddingtheedgeu1u2.ThenR*(G4)>R*(G3). LetH3=G[V(G3)(V(Cp)-w)],H4= G[V(G4)(V(H3)-w)].Then Similarly,bydirectcalculation,wehave: [1]BondyJA,MurtyUSR.Graphtheorywithapplications[M].NewYork:Macmillan,1976: 16-93. [2] Liu J B,Zhang S Q,Pan X F,et al. Bicyclic graphs with extremal degree resistance distance [EB/OL].(2016-01-03)[2016-12-28].http://www.arXiv:1606.01281v1.com/2016/01/03/bicyclic-graphs-with-extremal-degree-resistance-distance/. [3] Bonchev D,Balaban A T,Liu X,et al. Molecular cyclicity and centricity of polyclic graphs I cyclicity based on resistance distances or reciprocal distances [J]. Int J Quantum Chem,1994,50: 1-20. [4] Klein D J,Randic M. Resistance distance [J]. J Math Chem,1993,12: 81-95. [5] Gutman I,Feng L. Degree resistance distance of unicyclic graphs [J]. Trans Comb 1,2012,1: 27-40. [6] Chen H Y,Zhang F J. Resistance distance and the normalized Laplacian spectrum [J]. Discr Appl Math,2007,155: 654-661. [7] Palacios J L,Renom J M. Another look at the degree-Kirchhoff index [J]. Int J Quantum Chem,2011,111:3453-3455. [8] Palacios J L. Upper and lower bounds for the additive degree-Kirchhoff index [J]. Match Commun Math Comput Chem,2013,70:651-655. 2016-11-17 *通讯作者 洪运朝,研究方向:图论;E-mail:331963706@qq.com 朱忠熏(1973-),男,副教授,博士,研究方向:图论;E-mail:zzxun73@mail.scuec.edu.cn 国家自然科学基金资助项目(61070197);中南民族大学中央高校基本科研业务费专项资金资助项目(CZQ10007) O A 1672-4321(2017)02-0148-07 具有乘积度-基尔霍夫指标极值的双圈图 朱忠熏,洪运朝*,罗阿木,王维峰 (中南民族大学 数学与统计学学院,武汉430074) 距离;乘积度-基尔霍夫指标;双圈图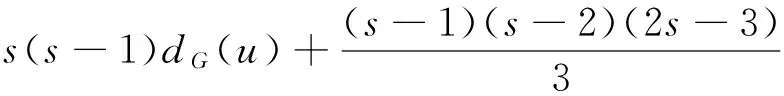

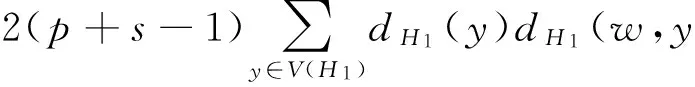

2 Main results
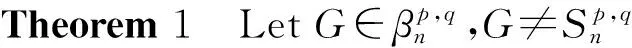


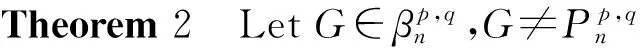



3 Bicyclic graphs with extremal multiplicative degree-Kirchhoff index