金婷婷，刘 东

（湖州师范学院理学院，浙江湖州313000）

Schrödinger Virasoro代数上的Poisson结构

金婷婷，刘 东

（湖州师范学院理学院，浙江湖州313000）

研究李代数上的Poisson代数结构问题是代数学研究中的一个重要问题.基于扭Heisenberg Virasoro代数的相关结果，利用根系阶化的方法首先给出Schrödinger Witt代数的所有Poisson代数结构，进而确定出Schrödinger-Virasoro代数上的所有Poisson代数结构.该研究成果对于进一步研究其他相关代数上的Poisson代数结构有重要作用.

Poisson代数；Schrödinger Virasoro代数；Witt代数；Virasoro代数

MSC 2010：17B60，17B63，17B65

无限维李代数的结构和表示理论对数学领域及物理学的发展都有极其重要的作用和影响.20世纪初，法国数学家E.Cartan给出了四类无限维李代数，其中Virasoro代数是Witt代数的泛中心扩张，是一类非常重要的无限维李代数，随后在Virasoro代数的基础上又衍生了许多其他的代数.1994年M.Henkel研究Schrödinger自由方程不变性时引入了Schrödinger-Virasoro代数的概念［1］.

Poisson代数源于Poisson几何的研究，具有代数结构和李代数结构，乘法与李代数乘法间满足Leibniz法则.近来许多人研究了结合的Poisson代数结构问题：姚裕丰研究了Witt代数和Virasoro代数上的Poisson代数结构［2］；靳全勤和佟洁研究了Toroidal李代数等李代数上结合的Poisson代数结构［3-4］；Kubo研究了特征零情形下有限维Poisson代数［5］，确定了仿射Kac-Moody代数上的所有结合的Poisson代数结构［6］；在Kubo的研究基础之上，靳全勤和佟洁系统地研究了扩张仿射Kac-Moody代数上的Poisson代数结构［7］.

目前，有关非交换、非结合的Poisson代数的研究较少.近来部分论文研究了Kac-Moody李代数、W（2，2），以及扭的Heisenberg-Virasoro代数上的非交换、非结合的Poisson代数结构［8-10］.本文在文献［9 -10］的基础上研究Schrödinger-Virasoro代数的Poisson代数结构.由于Schrödinger-Virasoro代数是Schrödinger-Witt代数的普遍中心扩张，因此本文首先给出Schrödinger-Witt代数的Poisson代数结构，进而确定Schrödinger-Virasoro代数上的Poisson代数结构.

在本文中，ℤ总表示整数集，ℂ表示复数域，所有的代数都定义在ℂ上.

1 基本概念

定义1.1［10］根据定义，Schrödinger-Virasoro代数L作为ℂ上的向量空间有一组基｛Li，Mi，Yp，C|i∈ℤ，p∈ℤ+1/2｝，且满足如下关系式：

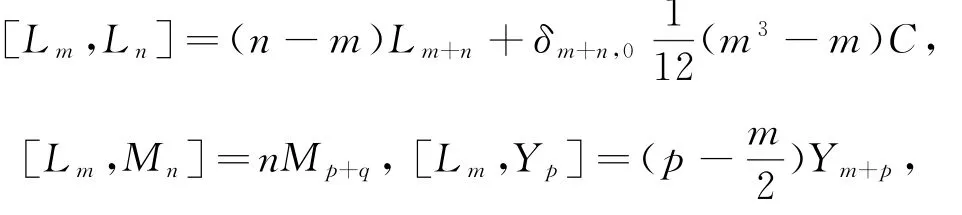
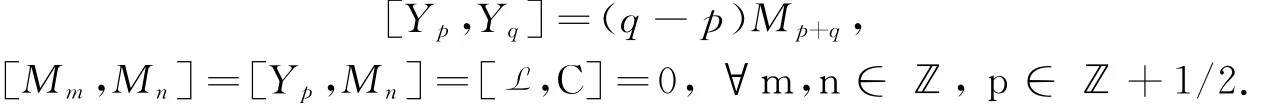
Schrödinger-Virasoro代数的由｛Li，Mi，C|i∈ℤ｝生成的子代数称为扭Heisenberg-Virasoro代数，记为H.近来Schrödinger-Virasoro代数表示理论得到了广泛研究［1114］.

Poisson代数源于Poisson几何的探究.它既是一个代数，又是一个李代数，且乘法与李代数乘法间满足Leibniz法则.

定义1.2［10］Poisson代数（A，*，［-，-］）是指ℂ上的一个向量空间A，同时具有代数乘法*以及李代数乘法［-，-］，且满足Leibniz法则：

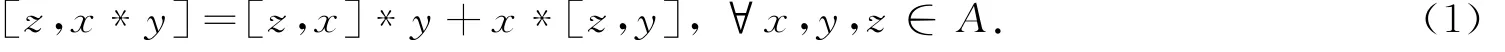
如果乘法*满足结合律，则称Poisson代数是结合的；如果乘法*满足交换律，则称Poisson代数是交换的.靳全勤和佟洁等主要研究了一些李代数上结合的或交换的Poisson代数结构［3-9］，但是非结合、非交换的相关问题研究较少.本文主要研究李代数Schrödinger-Virasoro代数上的一般Poisson代数结构（非结合、非交换），进而得到此代数上的结合或交换的Poisson结构.

定理1.1［10］若H是ℂ上的扭Heisenberg-Virasoro代数，则H上的任何Poisson代数结构满足：

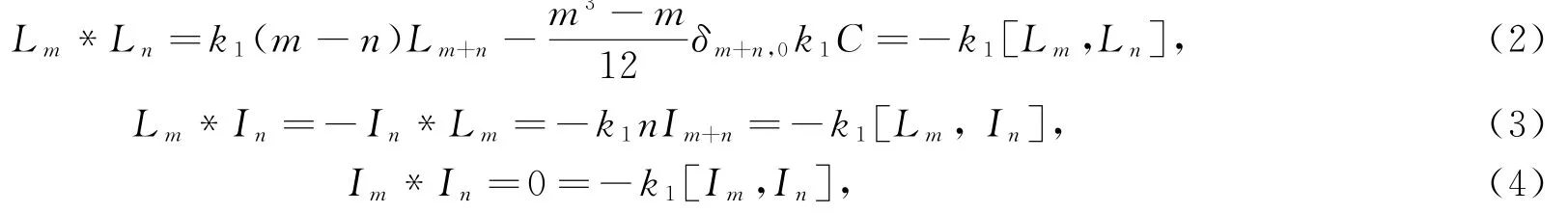
∀m，n∈ℤ，其余为零，其中k1∈ℂ.

2 Schrödinger-Witt代数上的Poisson结构

定义2.1［13］作为向量空间，Schrödinger-Witt代数Q：=ℂ｛Li，Mi，Yp|i∈ℤ，p∈ℤ+1/2｝，且对∀m，n∈ℤ，p∈ℤ+1/2满足如下关系式：

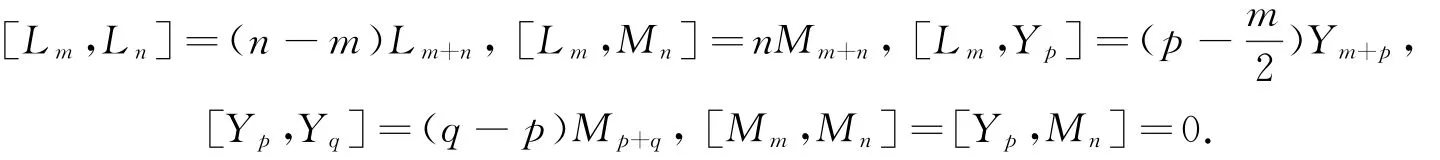
显然Q关于Cartan子代数h=ℂ｛L0，M0｝有分解［3］：

引理2.1 如果在Schrödinger-Witt代数Q上存在一个代数乘积*，使得（Q，*，［-，-］）成为一个Poisson代数，则有：

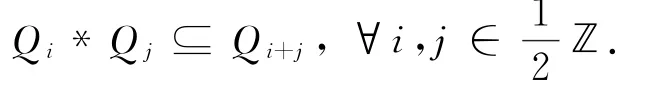
证明 对任意的x∈Qi，y∈Qi，有：

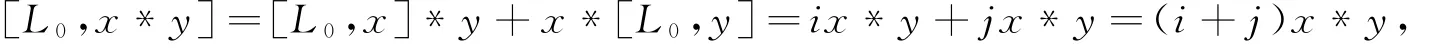
即x*y∈Qi+j，因此Qi*Qj⊆Q i+j.

定理2.1 Schrödinger-Witt代数Q上的任何Poisson代数结构满足：

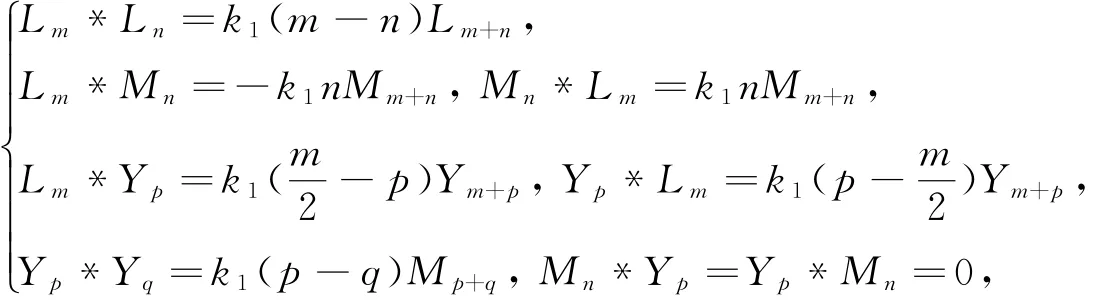
∀m，n∈ℤ，其余为零，其中k1为常数.

证明 Q关于Cartan子代数h=ℂL0有分解：根据引理2.1，Qi*Qj⊆Qi+j，同时根据定理1.1，可假设Lm，Im之间乘法满足（2）式～（4）式以及：

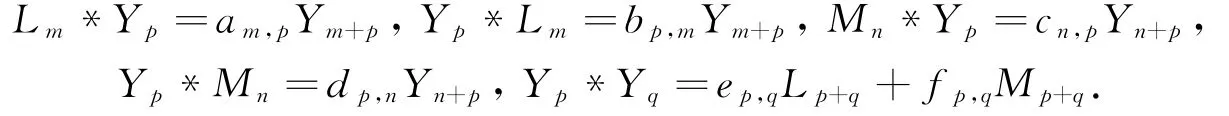
由于［Mk，Lm*Yp］=［Mk，Lm］*Yp+Lm*［Mk，Yp］=-k Mm+k*Yp，但［Mk，Lm*Yp］=am，p［Mk，Ym+p］=0.因此有-kcm+k，pYm+k+p=0，从而cm+k，p=0，即

类似上述讨论，由下列等式：

可推出

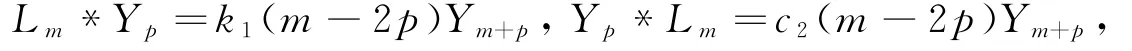
其中c2为常数.

由于

且

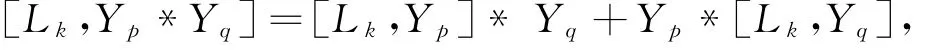
可推出Yp*Yq=c3（q-p）Mp+q，c3为常数.

注意到当m+k≠0时，

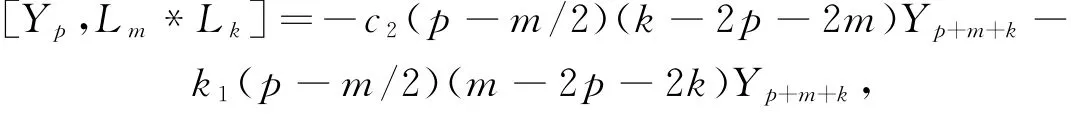
但

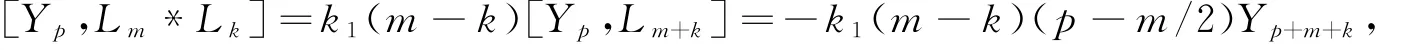
同样，由于

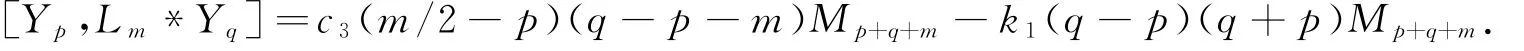
但

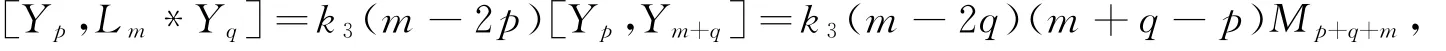
可推出k3=k1，c3=-k1.

于是有

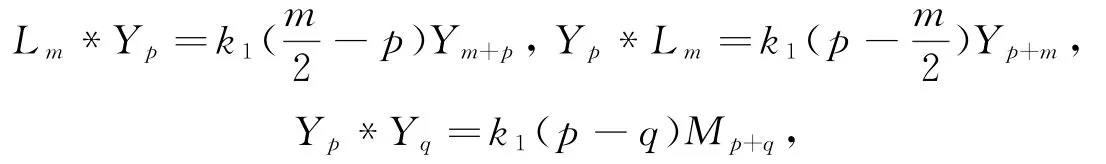
∀m∈ℤ，∀p，q∈ℤ+1/2，其中k1为常数.定理得证.

推论2.1 Schrödinger-Witt代数上没有非平凡的结合的Poisson代数结构.

3 Schrödinger-Virasoro代数上的Poisson结构

定理3.1 Schrödinger-Virasoro代数上的任何Poisson代数结构满足如下形式：

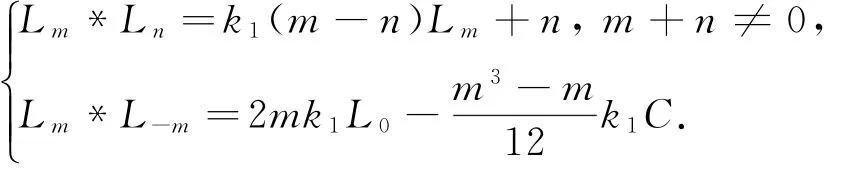
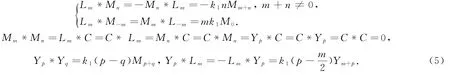
∀m，n∈ℤ，∀p，q∈ℤ+1/2，其中k1为常数.定理得证.

证明 显然Lm、Mm与Yp的Poisson乘法结构与定理2.1相同.

①讨论Lm与Mn的Poisson乘法结构.

当m+n≠0时，Lm*Ln，Lm*Mn，Mm*MnPoisson乘法结构与定理2.1相同.

当m+n=0且n≠0时，可假设：

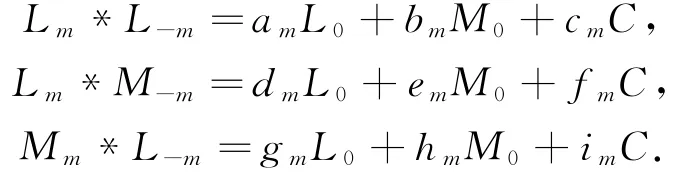
由于

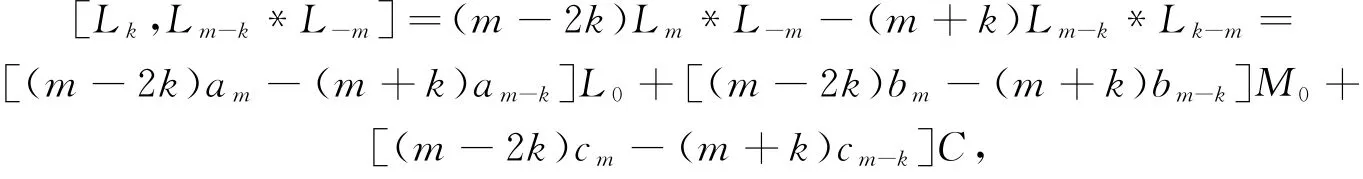
同时

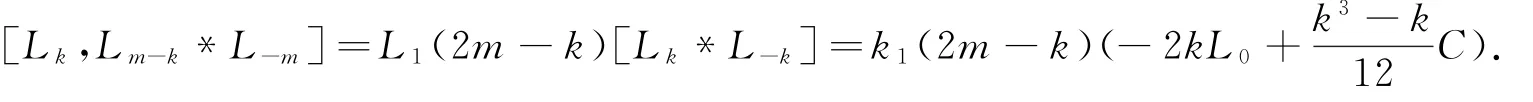
取k=-m，可推出

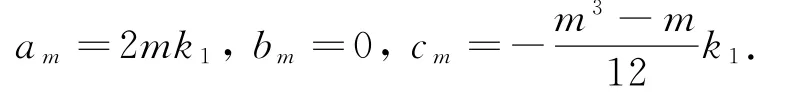
从而

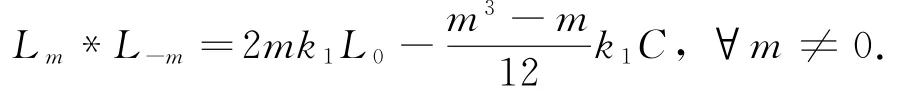
类似上述讨论，由等式：

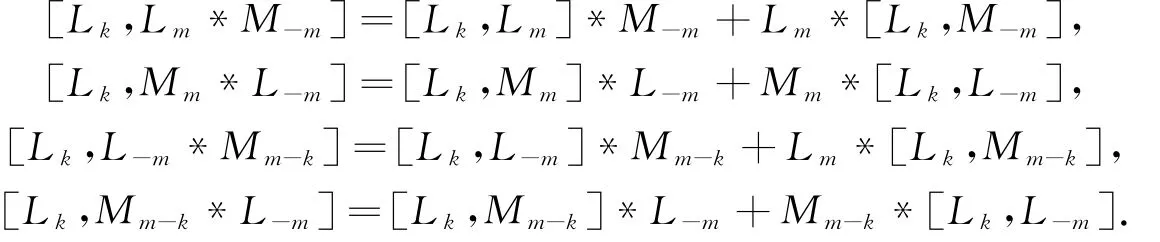
取k=-m，可推出

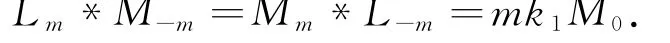
②讨论Lm，Mn，Yp分别与C的Poisson乘法结构.

由

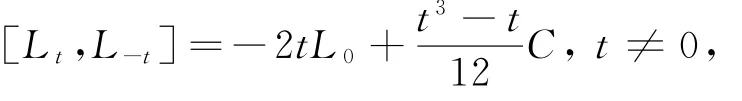
得：

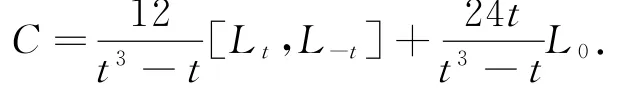
当m≠0时，有：

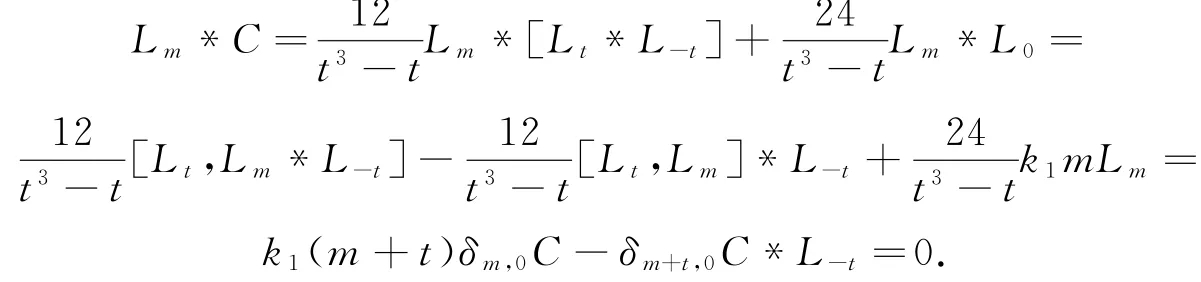
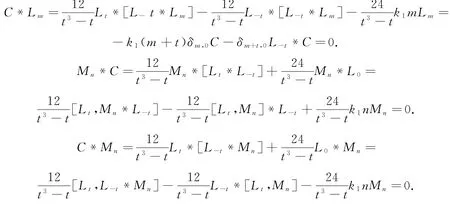
当m=0时，取k≠0，由于

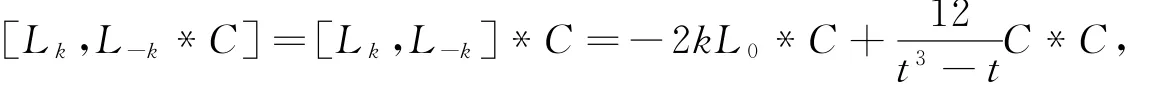
且

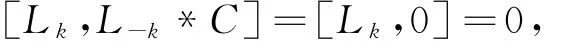
所以

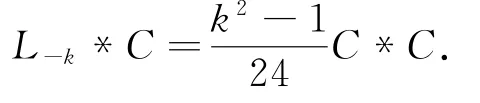
取k=1，得L0*C=0，从而Lm*C=0，∀m∈ℤ.类似上面的讨论，由下列等式：

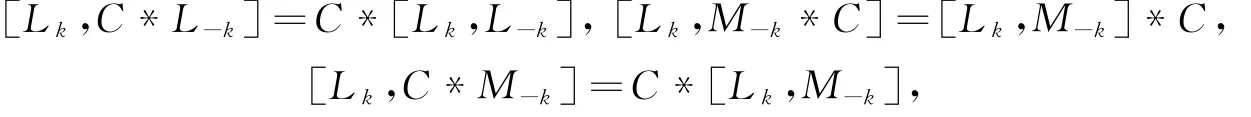
所以，对C*Ln=0，Mn*C=0，C*Mn=0，∀n∈ℤ.

当m=0时，注意到

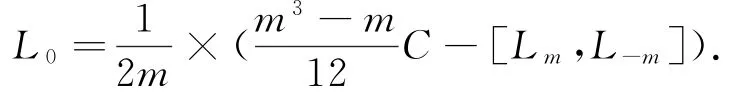
于是有：

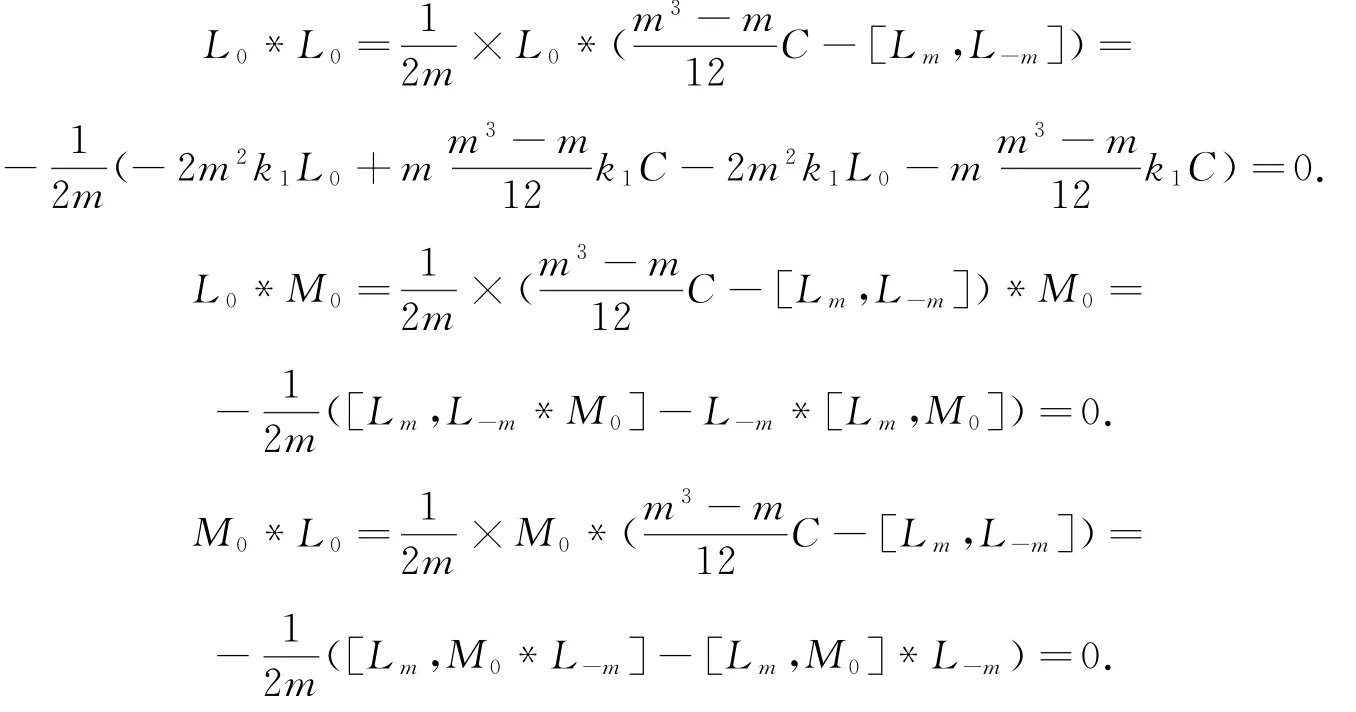
故对∀m∈ℤ，有：

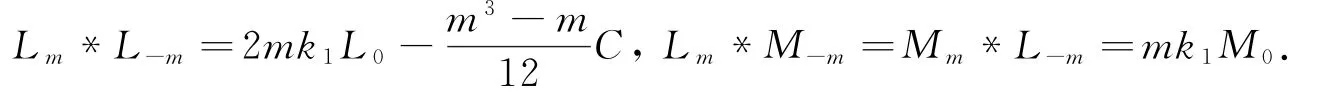
类似地，容易得到：

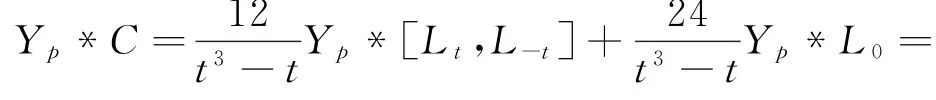
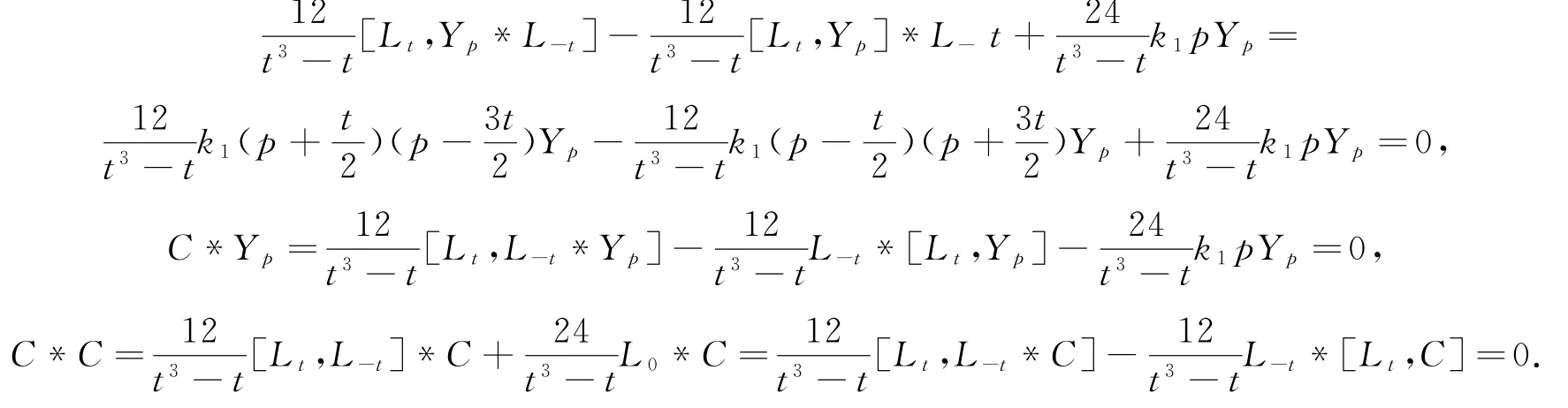
推论3.1 Schrödinger-Virasoro代数L上没有非平凡的结合的Poisson代数结构.

［1］Henkel M.Schrödinger invariance and strongly anisotropic critical systems［J］.J Stat Phys，1994，75：1 023-1 029.

［2］姚裕丰.Witt代数和Virasoro代数上的Poisson代数结构［J］.数学年刊，2013，34A（1）：111-128.

［3］靳全勤，佟洁.Toroidal李代数上的Poisson代数结构［J］.数学年刊，2007，28A（1）：57-70.

［4］佟洁，靳全勤.李代数的Poisson代数结构Ⅱ［J］.数学杂志，2010，30A（1）：145-151.

［5］KUBO F.Finite-dimensional non-commutative Poisson algebras［J］.J Pure Appl Algebra，1996，113（3）：307-314.

［6］KUBO F.Non-commutative Poisson algebra struetures on affine Kac-Moody algebras［J］.J Pure Appl Algebra，1998，126：267-286.

［7］靳全勤，佟洁.广义仿射李代数上的非交换Poisson代数结构［J］.数学学报，2011，54A（4）：561-570.

［8］ZUSMANOVICH P A.Compendium of Lie structures on tensor products［J］.Journal of Mathematical Science，2013，199（3）：40-81.

［9］李雅南，高寿兰，刘东.李代数W（2，2）上的Poisson结构［J］.数学年刊A辑，2016，In press.

［10］赵晓晓，高寿兰，刘东.扭Virasoro-Heisenberg代数上的Poisson结构［J］.数学学报中文版，已录用.

［11］LI J B，SU Y C.Representations of the Schrödinger-Virasoro algebras［J］.Journal of Mathematical Physics，2008，49（5）：053512.

［12］LIU D.Classification of Harish-Chandra modules over some Lie algebras related to the Virasoro algebra［J］.J Algebra，2016，447：548-559.

［13］TAN S B，ZHANG X F.Automorphisms and Verma modules for generalized Schrödinger-Virasoro algebras［J］.J Algebra，2009，322（4）：1 379-1 394.

［14］ZHANG X F，TAN S B，LIAN H F.Whittaker modules for the Schrödinger-Witt algebra［J］.J Math Phys，2010，51（8）：083524，17pp.

Poisson Structure on the Schrödinger-Virasoro Algebra

JIN Tingting，LIU Dong
（School of Science，Huzhou University，Huzhou 313000，China）

It is important to determine Poisson algebra structures on a given Lie algebra.Based on such results on the twisted Heisenberg-Virasoro algebra，we firstly determine all Poisson structures on the Schrödinger-Witt algebra by the method of root-graded，and then do researches on the Schrödinger-Virasoro Algebra.The results can help to further determine Poisson structures on other relevant Lie algebras.

Poisson algebras；Schrödinger-Virasoro algebras；Witt algebras；Virasoro algebras.

O152.5

A

1009-1734（2016）04-0001-06

［责任编辑 高俊娥］

2016-03-04

国家自然科学基金项目（11371134，11201141）；浙江省自然科学基金项目（LZ14A010001，LQ12A01005）.

刘东，教授，研究方向：李代数.Email：liudong@hutc.zj.cn

MSC 2010：17B60，17B63，17B65