☉湖北省秭归县归州镇初级中学　叶先玖



“旧瓶新装”，一种可行的编题方式

☉湖北省秭归县归州镇初级中学叶先玖

小专题教学，通常以思想方法为魂、题组训练为媒、计算推理为线来串联知识和方法，帮助学生获取基本的解题策略.因而，选择一些最有价值、最具代表性的、典范性习题，是习题课常用的教学套路.由于停留于表面认识，变式及生长不足，缺少系统归纳及共性提炼，看不透基本图形及性质，导致重复机械演练过度，结果是讲一题会一题，题目略微变式，学生仍觉困难.教学实践表明，“旧瓶新装”，是一种可行的借题生长方式，能有效提升学生的解题水平.本文以八年级下册教学中的一道选择题为例，从选择经典题、深度挖掘、继承经典、借题发挥等角度，呈现个人的一些做法及思考，抛砖引玉，探讨如何借用经典，催生出新题、新意、新机，最大限度地发挥经典习题的价值.

一、细觅“旧瓶”，发现经典

经典范例（2012年江苏省扬州市）如图1，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰Rt△ACD和Rt△BCE，那么DE长的最小值是_______.

选题说明：立意动态几何构思矩形小专题习题课时，笔者依托人教版八年级下册第64页的数学活动为素材，思考对第68页第13题进行改编，在查阅资料时，有幸选取到本题及2015年黑龙江省绥化市第9题，作为示例；精选2014年绥化市第11题、2015年绥化市第21题，2015年江苏省泰州市第16题、常州市第8题，2015年湖北省襄阳市第12题等五道题，作为习题跟进巩固，着力渗透分类讨论、翻折变化、方程思想、等积转化等方法，力求掌握有关解答折叠与最值等问题的基本策略.

二、慎审“旧瓶”，换装新衣

选题时，因为配备有参考答案，笔者并没有对上题作细致的解答，受参考答案先入为主的影响，备课时只预设了下面呈现的解法一.课堂中，在倾听学生交流时，学生却给出了更优化的解答.

1.审视解答

解法一：（函数求值法）如图1，设AC=x，则BC=2-x，因为△ACD和△BCE都是等腰直角三角形，所以∠DCA=45°，∠ECB=45°，可证得∠DCE=90°，从而得DE2=DC2+CE2=x2-2x+2.所以当x=1时，DE2取得最小值，DE也取得最小值，最小值为1.

解法二：（保角构造法）通常解答含特殊度数的角的几何题时，习惯于保全这个特殊角进行补形构建，从而转化成特殊图形进行解答.如图2，由∠A=∠B=45°，如果延长AD、BE交于点F，可得△AFB是等腰直角三角形，易证得四边形CDFE是矩形，则DE=CF，由垂线段最短可知，当CF⊥AB时，DE最小，结合三线合一及直角三角形斜边的中线等于斜边一半，求得DE的最小值为1.

解法三：（特殊位置法）上述两种解法严谨，无可挑剔，但作为一道选择题，费时不合算.不难看出，图中两个三角形的形状相同，而且随着点C的移动，两个三角形在AB上任何一点出现的机会均等，即两个三角形的地位是相等，因而，可采用特殊位置法，找出临界点，定位分析解答，显然就是AB的中点.此时有CD=CE，从而直接得到DE的最小值为1.

课后反思解法，此题虽小，但关联知识点、基本图形、数学方法较多，理应算是一道经典习题.

2.审视变式

课堂中学生的表现，引起了笔者对此题改编的兴趣.虽然本题只是一道3分的填空题，但从解法多样化角度看，本题可以说是思维含量较高的一道试题，有值得进一步研究并拓展的必要.经过研究发现，本题最大的特点，就是从“共点等边”图形为背景求线段值，考查的核心知识点是特殊图形的性质及勾股定理，由于解答思路不同，可以渗透不同的基本思想和方法，可以多角度进行改编.

外部基本图形变式：不难发现，在不改变题目条件下，单纯地更换图形形状，如图3，可以把两个等腰三角形换成两个等边三角形，从而得到最为经典也是常见的图形，通过作AF⊥CD，可以求出AD的最小值；如图4，更换为两个正方形，同样也能求出AF的最小值；类似地，还可以简单地更换“外衣”，用不同特殊图形去替换原题中的两个等腰三角形，得到不同的新题，其实本质及解答方法并没有变，从而让学生收获“对一题”而“会一片”的训练效果.

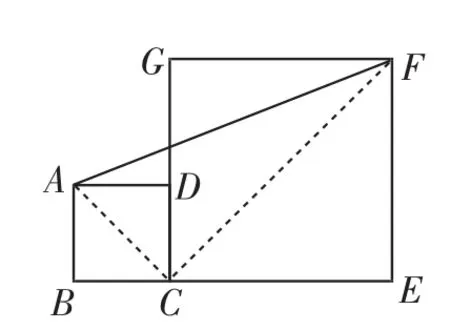
图4

内部基本知识变式：如果从图形旋转角度改编，如图5，线段AB的长为2，C为AB上一个动点，分别以C点为顶点，在AB的同侧作顶角为45°的等腰△ACD和△BCE.

（1）连接DE并求DE长的最小值.

（2）如图6，当C运动到AB的中点时，将△BCE绕C点逆时针旋转β（0°﹤β﹤135°），连接AE与BD交于点F.

①求证：AE=DB；

②当β=45°时，求DF的长.

图5

图6

解析：（1）由上述解法一可求得DE的最小值为1.（过程略）

（2）①C为AB的中点，可得AC=CD=CE=CB=1，∠ACD=∠ECB=45°，所以△ACD≌△ECB.由于△ECB是绕点C按顺时针方向旋转得到的，始终有AC=CE，CD= CB，∠ACD=∠ECB，又因为∠ACD+∠DCE=∠BCE+ ∠ECD，即∠ACE=∠DCB，由“边角边”可得△ACE≌△DCB，所以AE=BD.

②当β=45°时，证得四边形ACBF为菱形，BC=AC=1，△DCB为等腰直角三角形，所以得DF=BD-

三、拓展“旧瓶”，换装新意

适当更换条件，关联更多的知识点和方法，也可以进行如下深层次思想方法方面的融合，进行质的变式尝试，以期进一步提升思维含量.

1.着眼背景动态性

在组织正方形小专题时，着眼动态几何，复习最值问题，笔者重温上述经典范例，开发成通过定量计算，从而推理在正方形运动过程中，某一三角形成为等边三角形开放性说理题，以最大限度发挥上述经典题的价值.

改编题1：在直线BC上，线段BQ=12cm，C和D分别为直线BC上的两个动点，连接A D.

（1）如图7，分别以BC和CQ为斜边在同侧作两个等腰直角△BAC和△CMQ，连接AM，求出AM的最小值.

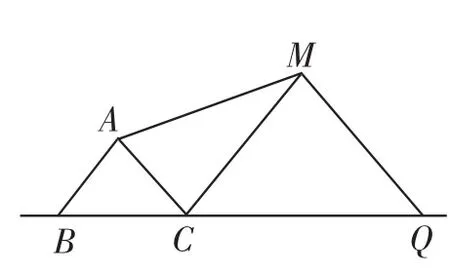
图7

（2）当C运动到BQ的中点处时，作等腰直角△BAC，D从C出发，在射线CB上运动，连接AD，以AD为边作正方形ADEF，连接CF.

①如图8，当点D在线段CB上时，探究BD与CF的关系并加以证明，指出点D在何处时，正方形面积最小？并求出这个最小值.

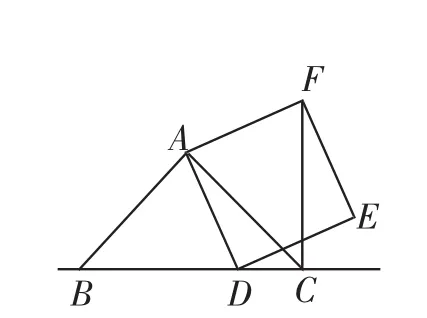
图8

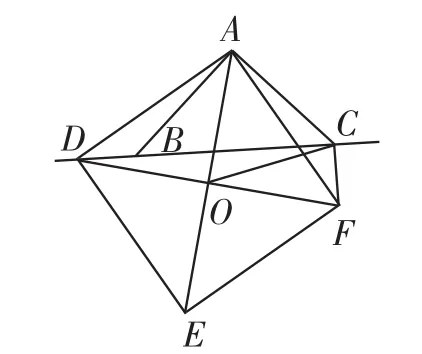
图9

②如图9，当点D在CB延长线上时，在BC下方作正方形ADEF，连正方形对角线交于O点，判断△AOC的形状，指出当点D运动到何处时，△AOC是等边三角形.

解析：（1）由上述三种解法可知AM最小值为6cm（过程略）.

（2）当点C运动到BQ的中点处时，可得BC=6.由∠BAD+∠DAC=∠DAC+∠CAF=90°，得到∠BAD= ∠CAF.又AB=AC，AF=AD，从而可证△BAD≌△CAF.所以BD=CF，∠FCA=∠ABD.而∠BAD+∠ACB=90°，所以∠ACB+∠ACF=90°，即∠BCF=90°，得BD⊥CF.由垂线段最短可知，当AD⊥BC时，正方形面积最小，由三线合一可知，此时D为BC的中点，可求得正方形的最小面积为9cm2.

（3）同（2）的方法可证得△BAD≌△CAF，得BD=CF，∠FCA=∠DBA.因为∠ABC=∠ACB=45°，得∠ABD= 135°，得∠FCD=∠FCA-∠ACB=90°.而由正方形的性质可知DO=OF=AO=OE，在Rt△DCF中，由∠FCD=90°及DO=OF可得OC=OF，从而可得OA=OC.由于点D在CB延长线上向左运动时，而点F是在垂直于BC的直线上运动，随DA长度不断增大，所以OA也随着增大，而AC长度不变，所以得△AOC是等腰三角形.当△AOC是等边三角形时，必有∠AOC=60°，得∠COF=30°，∠OCF=∠CFO= 75°，可得∠FDC=15°，从而得∠ADB=30°.过点A作AG⊥ BC于点G，由BC=6可求得，在△AGD和△AGB中，由∠ADB=30°，∠ABC=45°，可求得，得即D运动到距离B点时，有△AOC是等边三角形.

2.着眼问题的存在性

上述经典素材，从图形的对称性视角出发，着眼问题存在性的探究，可以再深度挖掘，以二次函数综合题与正方形为背景，立意三角形全等与相似、正方形性质、函数解析式等知识点，渗透分类讨论、待定系数法、运动与变化、数形结合、方程思想与转化等数学思想与方法的综合题，基于此，笔者就上题与2015年湖北省襄阳市第26题进行融会，改编成如下试题，作为九年级学生周测试题.

改编题2：如图10，在平面直角坐标系中，O为坐标原点，A（-2，0），Q是线段OA上一动点，D为OA的中点.分别以AQ、OQ为斜边作两个等腰Rt△AKQ和Rt△QHO，作直线KH交y轴于点G.

（1）当KH最小时，如图11，以OA长为边在第二象限作正方形ABCO，连接DC，将线段DC绕点D逆时针旋转90°得线段DE，以直线AB为对称轴的抛物线过C、E两点.求直线GD的解析式及抛物线的解析式.

（2）如图11，点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒，过点P作PF⊥CD于点F.试问：当t为何值时，以P、F、D为顶点的三角形与△COD相似？

（3）在（1）的条件下，M为直线AB上一动点，N为抛物线上一动点，是否存在点M、N，使得以M、N、D、E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由.

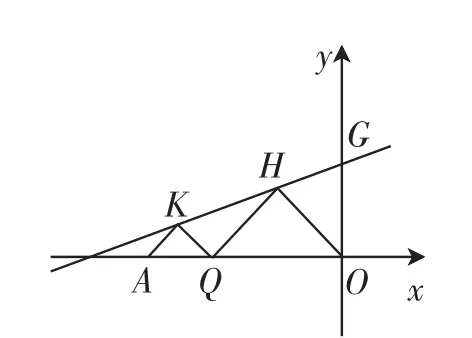
图10

图11

解析：（1）由前面解法易得M（0，1），又D（-1，0），可得直线GD的解析式为y=x+1；过点E作EL⊥x轴于L点，根据正方形的性质，可得OA=OC，∠AOC=∠DLE，根据余角的性质，可得∠OCD=∠LDE，可得△ODC≌△LED （AAS），所以EL=OD=1，DL=OC=2，点E的坐标为（-3，1）.因为抛物线的对称轴为直线AB即直线x=-2，所以可设抛物线的解析式为y=a（x+2）2+k，将C、E点的坐标代入可得抛物线的解析式为

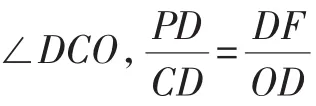
（3）分类讨论：可分▱MDNE、▱MNDE、▱NDME三种情况，根据一组对边平行且相等的四边形是平行四边，设M（-2，k）后，利用平移规律及抛物线解析式可求得对应的M、N的坐标.当四边形MDEN是平行四边形时，有MN∥DE，MN=DE，因此，当把D（-1，0）先向左平移两个单位，再向上平移1个单位可得到点E（-3，1），由这个平移规律可把M（-2，k）平移后得到点N（-4，k+1），再将N点的坐标代入抛物线的解析式中，求得k=1，从而得M1（-2，1），N1（-4，2）；同理，当四边形MNDE是平行四边形时，得M2（-2，3），N2（0，2）；当四边形NDME是平行四边形时，得

四、两点思考

1.精细识别，精心提炼经典

数学思想方法、能力的提升，正如张奠宙院士所言：需要每节课“细水滴灌”，每道题浸润，更得有专题式“大水漫灌”的渗透.而习题课，正是承担小专题教学的最好载体，是提升学生解题能力最有效的途径.通常，好题放在合适位置，才能发挥其价值，识别经典，选题编题是小专题教学必要的一步.选题编题要以学生学习可接受能力为本，守住教学要求的底线，积累题组，力求通法，少玩技巧，［1］以最大限度使用题目的训练功效.选择经典题进行小专题教学，可以分解大目标，分散难点，强化模式，落实小目标而实现总目标，提高解决问题的能力.一般而言，公认的经典题，在探讨多种策略求解时，会发现题目无论是从知识深度、广度和完整度，还是基本思想方法，一定会多角度关联，［2］或关联多个核心知识点，或蕴含着多种基本思想方法，或有基本图形等，因而才会沉淀并流传下来.如本文中的范例，虽然题小，如果从探究解法、图形变式入手，会收获化动为静、数形结合等转化策略；积累从局部到整体，通过补形构造，利用矩形性质进行转化的经验；甚至于通过图形位置相同的特性，采用特殊点位置这一特殊方法，到用函数思想最值一般性的解法，养成多视角自由切换的思考意识.在完成解答过程中，探究熟悉特殊图形性质，紧扣变与不变关系和数量，在温故的同时，吸取解题营养，提升分析和解决问题的能力.扣住经典范例中共点等边两个等腰直角三角形放缩的特性，可以进行外观简单的图形变式，实现“做一题，会多题，会一法，得多法”的目的.

2.精致拓展，精彩生长经典

课本习题及中考题，犹如“金矿”，是专家及命题人精心编制，是命题人智慧和心血的结晶.一些好题，堪称经典，是习题课范例的首选素材，能有效地开发成题组.能被师生多年认可的经典，绝不是仅仅可以“旧瓶简装”，局限于从外观上进行图形变式，而是可以“旧瓶新装”，能多角度变式拓展或生长.经典题如同题根，“抓住一个题根，就等于抓住了这个题族、这个题群、这个题系”.抓根挖掘进行改编，可以追求大道至简，［3］显然，能成为经典，自身具有生长性、渗透性和实用性，可以“旧瓶新装”.如同本文的范例那样，在立足原题蕴含的数学思想方法的前提下，尊重原创命制意图，遵从命题严谨科学的原则，力求简约而不失本质，［4］可以从换装内部基本数学知识，或有意增设更多的基本思想方法进行质的变式.

精选、提炼、拓展经典，找到生长点，借题再生，“旧瓶新装”，让老题生根发芽，焕发新机，是一种可行的编题方式.“旧瓶新装”式的改编，可以进一步认识、提升经典，让经典更出彩；可以把握研究的方向，提升研究水平，助力专业成长；可以更好地关爱学生，为他们提供更优化的高质量的习题，帮助学生走出“题海”，提升他们的分析和解决问题的能力.

参考文献：

1.韩新正.中考压轴题的一种价值取向：平实、简约［J］.中学数学（下），2015（8）.

2.刘东升.关联性：一个值得重视的研究领域［J］.中学数学（下），2013（12）.

3.刘永东.简化·简至——数学小专题复习的设计与实施策略［J］.中学数学（下），2016（4）.

4.万广磊.删繁就简三秋树，领异标新二月花——一道压轴题的命制历程［J］.中学数学教学参考（中），2016 （1-2）.H