陆博 刘深泉刘宣亮

（华南理工大学数学学院，广州 510640）

神经元模型中混合模式振荡动力学研究进展*

陆博 刘深泉†刘宣亮

（华南理工大学数学学院，广州 510640）

混合模式振荡（mixed-mode oscillations以下简称MMOs）是产生于动力系统中的一种复杂的振荡模式，它在自然界中是普遍存在的.混合模式振荡由一系列的小振幅的振荡和大振幅的振荡共同组成，两种模式的振荡交替出现.文章介绍了在神经元系统中混合模式振荡的研究情况和研究方法，主要分析几何奇异摄动理论在动力系统中混合模式振荡的产生机理的作用，并且介绍前包钦格复合体、内嗅皮层的星状细胞和垂体细胞神经元及腺体细胞的混合模式振荡的动力学研究，简单说明其他神经元模型的混合模式振荡的研究情况.为以后的其他领域的混合模式振荡的研究提供了方法.

神经元模型， 混合震荡模式， 几何奇异摄动理论， 鸭解， 张弛震荡

引言

混合模式振荡（mixed-mode oscillations，MMOs）是产生于动力系统中的一种复杂的振荡模式，它在自然界中是普遍存在的.混合模式振荡由一系列的小振幅的振荡和大振幅的振荡共同组成，两种模式的振荡交替出现.混合模式振荡100年前在化学反应中被第一次观察到［1］，直到在20世纪70年代，Belouzov-Zhabotinsky化学反应中的混合模式振荡才被仔细的研究［2-7］.除此之外，科学家在许多领域也发现了混合模式振荡，例如表面化学反应［8，9］、电化学系统［10-12］、神经元系统［13-16］、钙系统［17-18］、心电动力系统［19］、激光系统［20］和电子电路系统［21］等.

一些神经元模型也被用来研究混合模式振荡现象，例如Hodgkin-Huxley模型［22-24］、垂体细胞模型［25-27］、多巴胺神经元模型［28-29］、中间神经元模型［30-31］和一些神经网络，如前包钦格复合体［32］等.这些模型主要聚焦于研究离子通道在混合振荡中的作用以及混合模式振荡产生的动力学机理.

混合模式振荡的功能一直是一个很重要的问题.阈下（膜电位）振荡的功能被认为是一个定时装置［33］，在空间认知中起着重要的作用［34］.基于动作电位是神经元的基本信号的机理混合模式振荡中插入阈下振荡也许能对创造一个更有利于神经元之间信息交流的时间尺度有帮助.

通常如果混合模式振荡由s个小振幅振荡和L个大振幅振荡组成，用符号Ls来描述这种振荡模式［35-36］.混合模式振荡模式可以是规则的，也可以是不规则的.规则的混合模式振荡是周期的，所以符号Ls可以表示整个振荡的状态.如果混合模式振荡是不规则的，则可以用序列L1s1-L2s2…-LNsN（N是某一整数）来表示.而且不规则的混合模式振荡也可能是随机的或者混沌的.

如果出现了L0（L＞1）形式的振荡模式，即在两个或者更多的峰之间并没有小振幅的阈下振荡，习惯上称这种情况为簇发放形式［37-40］.间内和尖峰的频率可能是在相同的频率范围内，或不取决于神经元的类型及其他参数值.

动力系统理论用于研究微分方程解的定性性质.动力系统理论通过研究了平衡点和周期轨道的分岔，描述这些限制取决于系统参数设置.但是混合模式振荡的问题，超越那些标准/经典的一般动力系统理论.具体来说，人们试图剖析小振幅振荡和大振幅振荡的时间范围，识别这些几何对象在系统的状态空间，并确定状态之间如何转换.

早期的关于模型混合模式振荡的研究主要局限在在对混合模式振荡的进行分类，并且通过参数的变化观察振荡模式的变化情况.Hudson等［41］通过实验观察Belousov-Zhabotinsky振荡反应（简称BZ反应）中的混合模式振荡.Bakeš等［42］发现在pH化学反应中，随着流率的改变，系统从周期区域进入混沌区域时会产生混合模式振荡.Baba和Krisher［43］对原生具有全局耦合的电化学模型进行研究，通过数值计算得到了由其导出的齐次系统产生的混合模式振荡.Higuera等［44］研究发生在椭圆容器流体表面的法拉第波的单模式扩张模型，这个模型是一个奇异摄动问题，他们利用数值计算得到了表面波中的周期和非周期的混合模式振荡.

Barkley［45］最早跳出这个局限，他评估多时间尺度模型对混合模式振荡产生的能力.Barkley［46］又对从化学实验中产生的混合模式振荡与刻画该化学反应的七维数学模型中产生的混合模式振荡做了比较，该模型中有3维的多时间尺度模型. Barkley研究的混合模式振荡某些方面类似于一个鞍焦平衡点的同宿轨道.特别的，小振幅振荡的产生是由于轨线沿着不稳定流形远离平衡点.这种类型的同宿轨曾被L.Shilnikov［47］研究.但Barkley指出，混合模式振荡的出现并继续存在在开放区域的系统参数，而不是沿着参数空间余一维子流形.但是他不能给出一个具有这些特征的三维模型. Rubin等［48］研究了修正的三维经典Hodgkin-Huxley神经元模型的混合模式振荡，并研究了大小振幅的数目的变化，接着利用几何奇异摄动理论研究了混合振荡的产生的机理，并指出模型生成混合模式振荡的关键的系统参数.

Krupa等［49］分析哺乳动物脑干中多巴胺神经元双舱室模型的混合模式振荡产生的机理并指出混合模式振荡与鸭结构的关系.Desroches等［50］发展了计算方法来研究自耦合的FitzHugh-Nagumo（FHN）模型混合模式振荡产生的机理，该方法能精确地找出一些系统中的鸭解和混合模式振荡.

1 几何奇异摄动理论

1.1 Fenichel定理

混合模式振荡多产生于有着不同时间尺度的动力系统.此类系统的不同状态变量的变化速率有着较大的不同，在动力学中将此类动力系统视为奇异摄动问题.它本身是一个快-慢动力系统.几何奇异摄动理论（Geometric Singular Perturbation Theory简记为GSPT）采用几何的观点，从不变流形、奇异点的规范型等角度对此类系统进行分析研究［51-55］，其奠基工作称为Fenichel理论［52］.此外，一些学者还利用例如匹配展开的渐进方法进行分析［56-57］，还有法国斯特拉斯堡的一些数学家采用非标准分析对快-慢动力系统有着一些重要的发现［58-59］.本文主要介绍几何奇异摄动的相关概念和观点.考虑系统：

其中，x∈Rm，y∈Rn是状态空间变量，ε是一个远远小于1的正小参数，表示不同时间尺度的比例.函数f：Rm×Rn×R→Rm与g：Rm×Rn×R→Rn是无穷次可微的两个函数.习惯上，变量x称为快变量，变量y称为慢变量.如果做变换τ＝εt，则系统（1）可变为：

在（2）中令ε→0得

此系统称为快子系统，也称为层问题（layer problem），表示快变量的变化过程.显然在（3）中慢变量是一个常数，因此快子系统的解在相空间（x，y）中的轨线是一条直线，称为快纤维（fast liber）.同样的，在系统（1）中令ε→0得到慢子系统，也称为约化问题（reduce problem）：

系统（4）是一个微分代数方程组.它反应了慢变量的变化过程.几何奇异摄动理论的一个目标就是用（3）和（4）的解来刻画整个带有摄动的奇异问题的解的性质.而且可以看出（4）中的代数方程对应的（超）曲面为：

称为临界流形（或退化流形）.显然S中的点是系统（3）中第一个方程的平衡点.

定义1.1 如果在M上Jacobi矩阵Dxf（x，y，0）的特征值的实部不等于0，称流形M⊂S是法向双曲的.进一步，如果矩阵Dxf（x，y，0）在M上所有特征值实部小于0，就称M为吸引的；如果矩阵Dxf（x，y，0）在M上所有特征值实部大于0，就称M为排斥的；如果法向双曲流形M既不是吸引的，也不是排斥的，就称M是鞍型的.

对于法向双曲的流形M，有如下的定理：

定理1.1 （Fenichel定理）［52，60］设M⊂S是一个紧的法向双曲的子流形（可能有界），f，g∈Cr，r＜∞.则对充分小的ε＞0下列结论成立：

（1）存在一个局部不变流形Mε微分同胚于M.局部不变的意思是Mε具有轨线进入或离开所穿过的边界.

（2）Mε距M有一个O（ε）的Hausdorff距离.

（3）当ε→0时，上的流收敛于慢流.

（4）Mε是Cr光滑的，0＜r＜∞.

（5）Mε是法向双曲的，并且对快变量x与M有相同稳定性质（吸引、排斥或者鞍型）.

Mε也称为Fenichel流形，它是一类慢流形. Fenichel定理保证了对充分小的参数ε＞0，如果约化问题的临界流形是法向双曲的，那么带有扰动的摄动问题（1.1）与相应的约化问题有相同性质的临界流形，而且对快变量有相同地稳定性.进一步，Mε可以表示成一个函数图像，当法向双曲的条件被满足时，雅克比矩阵Dxf（x，y，0）在M上的任意点处皆是可逆的，由隐函数定理可知M可以表示成关于y的一个显函数，利用渐近展开法这个函数可以近似求出，这样问题（1.1）就可以限制在Fenichel流形上化为正则的摄动问题.

1.2 折点

混合模式振荡对应的多时间尺度的问题虽然是奇异摄动问题，但是有一些点不满足上述的法向双曲的条件，称之为折点（fold point）.正是这些点的存在，才有了张弛震荡、鸭现象和混合模式振荡等复杂的现象产生.下面我们对这样的折点进行分类.为了简单起见我们取m＝1，n＝2，系统可以写为：

相应的临界流形为：

此时临界流形是三维空间中的一张曲面.相应的S上的折点组成的集合是S对应的曲面上的一条（或几条）曲线，有如下的定义：

定义1.2 临界流形S称为是（局部）有折的，如果存在一个集合F有如下的形式：

其中F中的点称为系统（5）的折点.更高维的情况可以参看文献［61］.

正如在1.2节中的分析，通过几何奇异摄动理论的思想，系统（6）也可以通过相应的快子系统和慢子系统来进行研究.注意到快子系统的解在相空间中是一条直线，那么注意力就集中在慢子系统上来进行研究.（6）相应的慢子系统为：

在（8）的第一个方程两端进行微分，并将（8）的后两个方程代入移项可得：

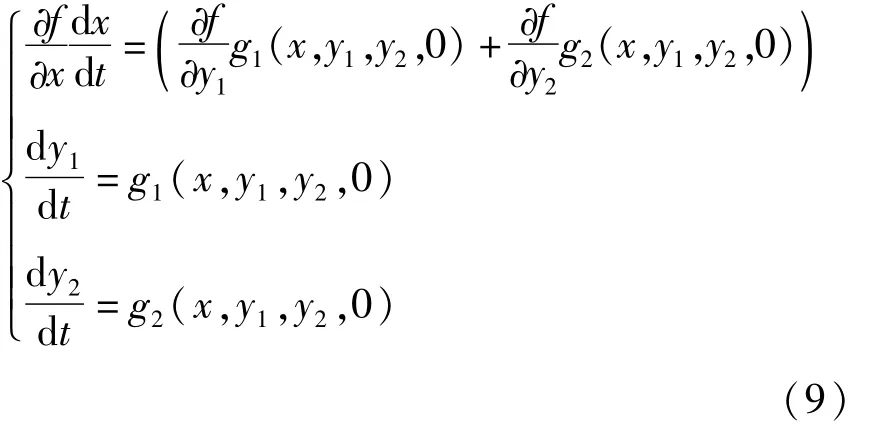
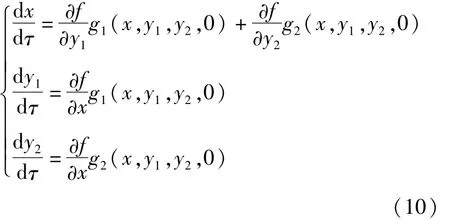
系统（10）与系统（9）在相平面上有相同的轨线，只是方向相反.满足条件

的点p*（x，y1，y2）成为折奇异点.并且有如下的定义：

定义1.3 设λ1，λ2是限制在临界流形S上的雅克比矩阵在点p*的特征值，

（1）若λ1，λ2是实数，且λ1λ2＜0，则称p*是折鞍点（fold saddle）；

（2）若λ1，λ2是实数，且λ1λ2＞0，则称p*是折结点（fold note）；

（3）若λ1，λ2是虚数，且λ1λ2＞0，Im（λ1，2）≠0，则称p*是折焦点（fold focus）.

注：如果有两个特征值相等且同为实数，则称为退化的折结点，如果两个特征值为实数且只有一个等于零，则会产生折鞍结点分岔现象.系统在这些折点处会产生奇异鸭解，混合模式振荡等现象.

1.3 张弛震荡与鸭解

张弛震荡是发生在多时间尺度的动力系统中的一种周期轨线，它的特征是这个周期轨线由快慢两部分相互重复连接组成.比较典型的张弛震荡是在Van der Pol方程中［62］.产生张弛震荡的动力系统因为有多个时间尺度，因此可以用几何奇异摄动理论对其进行研究.下面用二维FitzHugh-Nagumo型神经元模型［36］来说明张弛震荡的产生过程.考虑如下的方程组：

其中，v表示类电压变量（类似于HH方程中的膜电位），w表示恢复变量（类似于HH方程中门控变量），I是外界刺激，ε，γ和λ是常数且0＜ε≪1.图1展示了FitzHugh-Nagumo模型中的张弛震荡，从图1可以清楚的看出，随着参数ε→0，模型的周期轨线逐步向临界流形和快纤维组成的闭合轨线逼近，期极限状态下的周期轨线即为张弛震荡.

按照在1.1节的分析，首先将FitzHugh-Nagumo模型分成层问题和约化问题.约化问题的解位于临界流形上，即图1中的AB段和CD段.层问题的解（快纤维）对应于周期轨中时间快尺度的问题，即为图1中BC段和DA段.B和D为折点，也称为跳跃点.整个张弛震荡的产生过程是这样的，首先系统沿着临界流形的吸引部分从A到B，在B点产生跳跃沿快纤维到达C点，然后再次沿着吸引部分从C点走到D点，由于D也是一个跳跃点，因此在D点出再次沿快纤维到达A点，形成张弛震荡.因此张弛震荡的产生可用快慢两个子系统进行分析，在折点处的分析可以借助于近年来发展的blow-up技术.由于折点处法向双曲的性质已经被破坏，前面的理论很难对折流形处的奇异点进行分析.Blow-up技术的思想是通过一组巧妙的坐标变换，将折上的奇异点变换成一个球面，通过引入合适的坐标卡，使blow-up后的向量场有更容易研究的性质，具体的做法可以参看文献［63-65］.

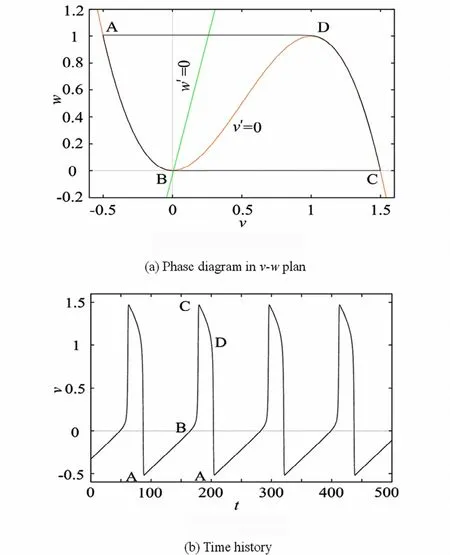
图1 ε＝0.001，γ＝4，λ＝0.02时，FitzHugh-Nagumo模型的解在（v，w）平面的相图和时间历程Fig.1 Phase diagram and time history of the solutions for FitzHugh-Nagumomodel in v-w plan when ε＝0.001，γ＝4，λ＝0.02

图2 系统（11）的鸭解在参数I（外界刺激）的改变下的变化图（a）I＝-0.221752，（b）I＝-0.22176，（c）I＝-0.22175192，（d）I＝0.21Fig.2 Relationship of canard-parameter I（external stimuli）（a）I＝-0.221752，（b）I＝-0.22176，（c）I＝-0.22175192，（d）I＝0.21

鸭解（canard）指的是同时包含吸引部分和排斥部分的奇异摄动系统的解.一维的孤立鸭解也称为鸭环.在奇异摄动系统中，鸭解沿着慢流形的吸引部分穿过折点（或折点附近），然后继续沿着慢流形的排斥部分形成周期解.由于在二维系统中这些周期解对应的轨线在相空间中形状类似于“鸭”，因此称这类解为鸭解.根据相空间周期轨线的形状可进一步分为有头鸭和无头鸭两种情况.

鸭解的一个普遍特征是周期解的振幅随着控制参数的微小改变而产生巨大变化.超临界Hopf分支出的小周期轨随着控制参数的改变迅速的变成大的松弛环，这种Hopf分岔附近的周期轨振幅快速增大的现象称为鸭爆破（canard explore）.鸭解就位于小的Hopf环与大的松弛环之间.由于鸭爆破现象的存在，因此鸭解很难被观察到，因此很多学者致力于从理论上证明奇异摄动系统中鸭解的存在性.几何奇异摄动理论的观点认为鸭解的存在性决定于摄动系统的慢流形的吸引部分（记为Sa，ε）与排斥部分（记为Sr，ε）是否在折点附近相交.

按照Wechselberger［61］等的观点，在慢流形上，有限时间内从吸引部分Sa穿过折点到排斥部分Sr形成的鸭解称为奇异鸭解；带摄动的系统在慢流形附近从吸引部分Sa，ε穿过折点到排斥部分Sr，ε形成的鸭解称为最大鸭解.

结合1.2折点的分类，可以进一步分析奇异鸭解的类型.折焦点处不会产生奇异鸭解.折焦点处的流的方向只有沿着折的时候才会发生改变，所有开始于折焦点附近的解会在有限的正向或反向时间内到达折点组成的集合，并在此处发生爆破.对于折鞍点的情形，折鞍点处存在中心稳定流形Wcs和中心不稳定流形Wcu，他们产生出唯一的快纤维分别记为Ws和Wu，快纤维Ws和Wu分别在折点处与对应的稳定与不稳定特征向量相切.而对于慢子系统的约化流可以通过改变去奇异化慢子系统在慢流形排斥部分的方向得到.快纤维和慢子系统的约化流就可以拼凑成系统的鸭轨线.开始于稳定快纤维Ws的约化流的轨线在有限时间到达折奇异点处并穿过折点与不稳定分支Wcu相交.这种类型的奇异鸭解称为折鞍点型（fold saddle type）.开始于Sa的其他的约化流的轨线或者在有限时间内到达折点发生爆破，或者根本到达不了折点.而开始于不稳定快纤维Wu的轨线会相反的穿过折点从Sr到达Sa，这样的鸭解也称为伪鸭解.对于折结点的情形，如果两个特征值都是负的，此时系统只有稳定的中心流形Wcs，定义Wss为唯一快纤维的子集相应于强稳定特征向量沿着折张成的空间，而慢子流形的约化流仍通过去奇异系统来得到.集合Wss与折点组成的集合F在Sa上围成的区域称为奇异漏斗（singular funnel），奇异漏斗中的每一条轨线都是一个奇异鸭解.开始于Wss上的轨线在有限时间内到达奇异点集但是相交正切于相应折结奇异点的强稳定特征向量.开始于Sa上的其他轨线到达折点集在有限的时间内并在有限时间内爆破.对于奇异摄动的最大鸭解的存在性也有如下的定理：

定理1.2［61］对于奇异摄动系统（1.1）当ε充分小时，定义，下列结论成立.

（1）折焦点处没有最大鸭解产生；

（2）在折鞍点处，奇异鸭解的（n-1）维集合Wcs扰动到最大鸭解的（n-1）维集合；

（3）在折结点处，当0＜μ＜1时，（n-1）维奇异鸭解（也称为强鸭解）的集合Wss扰动到（n-1）维的最大强鸭解（也称为首要强鸭解）；

（4）在折结点处，若μ-1∉N，则奇异弱鸭解的（n-1）维集合扰动到（n-1）维的最大弱鸭解（也称为首要弱鸭解）；

（5）在折结点处，设k是一个正整数，且满足2k +1＜μ-1＜2k+3并且μ-1≠2k+2则除了首要鸭解外，还存在其他的k个最大鸭解，称为次要鸭解.

2 快慢动力系统中混合模式振荡的产生机理

混合模式振荡的生成需要各种机制的协调作用：（i）阈下振荡的生成机制，（ii）峰发放机制，包括峰的发生和峰发放形成的动力学描述，以及（iii）从峰发放状态到亚阈值状态的恢复机制.

能产生固有振荡的最小模型是一些二维的神经元模型，包含了两个动力学变量：电压v和恢复变量w［66］.这些模型可能产生亚阈值振荡或者峰发放，但是不能产生混合模式振荡.混合模式振荡需要额外的描述这两个状态之间动力学的变化的机理.这个机理可能由外部输入产生（对于非自治系统），例如在某种情况下慢流形穿过Hopf分岔和产生于强迫振荡性的模式［67］，或者来自于一个额外的自变量的变化（自治系统）产生的三维“鸭现象”［68］.

能够产生混合模式振荡的最小的模型是一个包含了多重时间尺度的三维的非线性方程组［36］.研究它可以得到很多基本的动力学性质.混合模式振荡的产生原理关键依赖于从亚阈值振荡到峰发放的变化机理.一些机理已经在被研究发现，此外关于“鸭解”现象与混合模式振荡的关系也被很多学者所研究［65，68-71］.这些结果在文献［60］中被总结出来.

利用几何奇异摄动理论的相关结果，在三维快慢动力系统中产生混合模式振荡的原因主要有折结点附近的最大鸭解的旋转和奇异Hopf分岔的产生，下面逐一进行讨论.

2.1 折结点导致的混合模式振荡

在1.3节中指明对于折结点附近会形成奇异漏斗，而在此处首要强鸭解会围绕首要弱鸭解产生旋转.此现象从几何的角度可以解释，强鸭解可以视为Sa，ε与Sr，ε相对位置改变的轨迹.开始于Sa，ε的轨线在走向同侧强鸭解时候受到了Sr，ε的限制，从而再次回到了Sa，ε，这样就形成了一次旋转.而弱鸭解可以看做是旋转中心.而开始于Sa，ε的轨线到达强鸭解另一端的时候，被Sr，ε阻止并沿着快纤维的方向再次回到Sa，ε.进入奇异漏斗的轨线被困入其中一段时间，然后跳出这个折附近沿着快纤维，然后全局回归机理保证了轨线会再一次回到Sa，ε的漏斗中.不断重复这个过程，混合模式振荡便产生了.轨线进入漏斗以后，在折结奇异点附近产生小振幅振荡，然后轨线跳跃到快纤维离开漏斗，再根据全局回归机理［72］轨线，再次返回漏斗形成周期的大振幅振荡，于是1s模式的混合模式振荡便形成了.

2.2 奇异Hopf分岔导致的混合模式振荡

混合模式振荡除了可以有折结点产生，许多研究结果发现混合模式振荡与奇异Hopf分岔也有关系.奇异Hopf分岔是摄动系统的Hopf分岔在ε趋于0时得到的.在快慢系统中，系统的平衡点可能在临界流形上的折的附近.如果在参数与相空间系统在距离折O（ε）处经历了的Hopf分岔，就习惯上称为奇异Hopf分岔［70，73-75］.这种Hopf分岔的特征值的虚部有着的量级，这个量级介于快时间尺度与慢时间尺度之间.在Hopf分岔附近，鸭周期轨的振幅会快速的增大，这种现象即为上文提到的鸭爆炸.奇异Hopf分岔存在与鸭爆破有紧密的联系.奇异Hopf分岔使得在平衡点附近产生小振幅的振荡，然后随着周期解振幅的突然增大使轨线沿着快纤维方向继续，然后由于全局回归机理形成大振幅振荡，所以也形成了1s的混合模式振荡.Guckenheime对具有两个慢变量的摄动系统中的奇异Hopf分岔进行研究，并研究了它与混合模式振荡的联系［70，76］.图3给出了一个典型的三维系统：

图3 由奇异Hopf点导致的混合振荡现象的示意图Fig.3 Sketch ofmixed mode oscillations caused by singular Hopf point

在式（12）中参数值取ε＝0.01，ν＝0.007，a＝-0.4，b＝-0.4和c＝1.15时由奇异Hopf分岔导致的混合模式振荡.在折点附近的奇异Hopf分岔使轨线沿小的极限环运动形成小振幅振荡，然后振幅迅速增大形成大振幅振荡，于是混合模式的振荡便形成了.

更高维的模型会产生更复杂的混合模式振荡现象.在基于电导的神经元模型中，由于离子通道对亚阈值振荡和峰发放状态有很大的影响，所以高维的模型很难分析混合模式振荡的产生机理，但这些模型的基本原理也可以化简成低维的模型来研究.

3 神经元模型中的混合模式振荡

3.1 內嗅皮层的星状细胞

内嗅皮层（entorhinal cortex，EC）是海马结构的输入与输出结构，在大脑新皮质与海马之间起双向的信息传递作用，按空间结构可分为外侧内嗅皮层（LEC）和内侧内嗅皮层（MEC）［77］.内侧内嗅皮层共分为6层，其中第Ⅰ和第Ⅳ层为非细胞层，Ⅴ层和Ⅵ为其深层，Ⅱ层和Ⅲ层为其浅层.EC的浅层神经元主要是接受大脑皮层（包括联合皮质、嗅周皮质以及海马旁回皮质）的传入，将这些认知和高度处理的感觉信息传递至海马结构.深层主要接受海马CAI和下托的输入，将其传回至新皮层，从而形成海马-EC-新皮层的情景记忆环路［78］.在内嗅皮层浅层中，锥体神经元（Pyramidal Neuron）和星型神经元（Stellate Neuron）是两类主要的投射神经元.因此，研究这两类细胞的基本电生理特性有助于揭示海马依赖性学习和记忆的机制.其节律振荡在θ（4～12赫兹）和γ（30～100赫兹）频段形成.内在的阈下（膜电位）振荡，θ和γ频率的混合模式振荡已在各种类型的神经元被观察到［79-82］.內嗅皮层第Ⅱ层星状细胞的混合模式振荡被广泛的研究［83-85］.

生理实验和数学模型的计算都表明，內嗅皮层第Ⅱ层的星型细胞能在-55mV附近产生阈下振荡.当收到外界超极化的直流刺激时，在阈下振荡以后也会有张弛震荡，也就是大振幅振荡产生.阈下振荡和张弛震荡交替出现，即产生混合模式振荡.混合模式振荡的产生与“鸭解”现象有关，对哺乳动物的记忆和空间感知有重要的作用.

3.2 前包钦格复合体

呼吸节律的产生部位和机制一直是神经生物学研究领域中的重要课题.近年来的研究表明，延髓头端一个被称为前包钦格复合体（pre-Bötzinger complex，PBC）的区域是哺乳类动物呼吸节律起源的关键部位.该区域位于疑核头端腹外侧，外侧网状核背内侧；在头尾方向上位于包钦格复合体与吻端腹侧呼吸组（Rostral ventral respiratory group）之间.进一步研究发现，在厚度仅为350μm、包含PBC的脑片上即可记录到舌下神经根（XII）的节律性放电；在PBC内微量注射高K+溶液后XX放电节律加快；注射兴奋性氨基酸受体拮抗剂CNQX则引起其放电节律减慢甚至消失.这些结果提示，PBC即是新生哺乳类动物呼吸节律起源的关键部位.此后的许多研究表明，PBC也存在于成年整体大鼠、猫及狗的延髓.大量研究表明，PBC是延髓呼吸中枢内在结构和功能方面具有相对特异性的部位，它在呼吸节律产生中起着关键作用；PBC参与呼吸节律形成的机制尚待进一步探讨.但利用Poincaré映射可以判定在PBC中的确能产生混合模式振荡［32］.

3.3 垂体细胞

混合模式振荡不但在神经元中被发现，在内分泌细胞如垂体细胞，胰腺β细胞中也被发现.垂体是位于丘脑下部的腹侧的卵圆形小体，也是身体内极为复杂的内分泌腺，所产生的激素不但与身体的生长有关，且可影响内分泌腺的活动.用近代的免疫荧光、组织化学等方法，结合电镜观察证明腺垂体由六种腺细胞组成.通过对垂体中分泌生长素、催乳素和促性腺激素的细胞进行膜片钳实验，并记录它们对应动作电位的时间历程，在其中也可以发现混合模式振荡的产生.

除此之外越来越多的混合模式振荡发现于神经元模型之中，例如Hodgkin-Huxley模型、FHN模型，多巴胺模型、LP神经元模型与中间神经元模型等.这些模型中混合模式振荡产生的机理也被广泛的研究.

4 总结

混合模式振荡作为一种复杂的动力学现象越来越多的引起了人们的关注.在神经元模型中由于混合模式振荡的生理意义一步步被揭开，也是其成为神经科学研究的一个热点.但是神经元自身的复杂性决定了刻画神经元的数学模型往往是高度非线性的高维动力系统.前文也提到高维的动力系统很难直接研究混合模式振荡产生的机理，所以高维模型就面临着降维的问题.常见的高维非线性系统的降维方法，有基于中心流形理论的降维方法、Lyapunov-Schmidt（L-S）方法、非线性Galerkin方法和POD方法快慢动力系统的降维等［86］.这些经典的局部降维理论即使对较低维系统，中心流形的求解和其它约化方法的计算也是十分困难.对于高维系统更是难以应用.文本介绍的奇异摄动理论主要应用于快慢动力系统.由于快慢动力系统动力学行为会发生在不同的时间尺度上，慢时间尺度上的变化描述系统的主要特征，而快时间尺度上的变化描述瞬态过程或者周期振荡.对于这类动力系统，可以通过消去快时间尺度上的维数来达到降维的目的，进一步研究混合模式振荡的产生机理，从而揭示神经元的生理活动.

1 Ostwald W.Periodic phenomena in the disintegration of chrome in acids.Zeitschrift Fur Physikalische Chemie-International Journal of Research in Physical Chemistry＆Chemical Physics，1900，35：33～76

2 Graziani K R，Hudson J L，Schmitz R A.The Belousov-Zhabotinskii reaction in a continuous flow reactor.The Chemical Engineering Journal，1976，12（1）：9～21

3 Hudson JL，Mankin JC.Chaos in the Belousov-Zhabotinskii reaction.Journal of Physical Chemistry A，1981，74：6171～6177

4 Maselko J，Swinney H L.A farey triangle in the Belousov-Zhabotinskii reaction.Physics Letters A，1986，119（8）：403～406

5 Roux JC，Rossi A，Bachelart S，et al.Experimental observations of complex dynamical behaviour during a chemical reaction.Physica D，1981，2（2）：395～403

6 Rachwalska M，KawczynskiA L.New types ofmixed-mode oscillations in the Belousov-Zhabotinsky reaction in continuously stirred tank reactors.Journal of Physical Chemistry A，1999，103：3455～3457

7 Brøns M，Bar-Eli K.Canard explosion and excitation in a model of the Belousov-Zhabotinsky reaction.Journal of Physical Chemistry，1991，95（22）：8706～8713

8 Bertram M，Beta C，Pollmann M，et al.Pattern formation on the edge of chaos，Experiments with CO oxidation on a Pt（110）surface under global delayed feedback.Physical Review E，2003，67（3-2）：210～215

9 BertramM，Mikhailov A S.Pattern formation on the edge of chaos：Mathematical modeling of CO oxidation on a Pt（110）surface under global delayed feedback.Physical Review E，2003，67：036207

10 Koper M T.Bifurcations of mixed-mode oscillations in a three variable autonomous van der pol-duffingmodelwith a cross-shaped phase diagram.Physica D，1995，80（1-2）：72～94

11 Plenge F，Rodin P，Scholl E，etal.Breathing current domains in globally coupled electrochemical systems：A comparison with a semiconductor model.Physical Review E，2001，64（5-2）：1725～1732

12 Moehlis J.Canards in a surface oxidation reaction.Journal of Nonlinear Science，2002，12（4）：319～345

13 Drover J，Rubin J，Su J，et al.Analysis of a canard mechanism by which excitatory synaptic coupling can synchronize neurons at low firing frequencies.SIAM Journal on Applied Mathematics，2004，65（1）：69～92

14 Makarov V A，Nekorkin V I，Velarde M G.Spiking behaviour in a noise-driven system combining oscillatory and excitatory properties.Physical Review Letters，2001，86（15）：3431～3434

15 Alonso A A，Llinás R R.Subthreshold Na+-dependent theta like rhythmicity in stellate cells of entorhinal cortex layer II.Nature，1989，342（6246）：175～177

16 Medvedev G S，Cisternas J E.Multimodal regimes in a compartmentalmodel of the dopamine neuron.Physica D，2004，194（3-4）：333～356

17 Kummer U，Olsen L F，Dixon C J，et al.Switching from simple to complex oscillations in calciumsignalling.Biophysical Journal，2000，79（3）：1188～1195

18 Rotstein H G，Kuske R.Localized and asynchronous patterns via canards in coupled calcium oscillators.Physica D，2006，215（1）：46～61

19 Krogh-Madsen T，Glass L，Doedel E J，et al.Apparent discontinuities in the phase-resetting response of cardiac pacemakers.Journal of Theoretical Biology，2004，230（4）：499～519

20 Marino F，Catalán G，Sánchez P，et al.Thermo-optical“canard orbits”and excitable limit cycles.Physical Review Letters，2004，92（7）：073901

21 Satyabrata C，Syamal K D.Shilnikov chaos and mixedmode oscillation in Chua circuit.Chaos，2010，20（2）：023107

22 Doi S，Inoue J，Kumagai S.Chaotic spiking in the Hodgkin-Huxley nervemodelwith slow inactivation in the sodium current.Journal of Integrative Neuroscience，2004，3（2）：207～225

23 Rubin J，Wechselberger M.Giant squid-hidden canard：the 3D geometry of the Hodgkin-Huxleymodel.Biological Cybernetics，2007，97（1）：5～32

24 Rubin J，Wechselberger M.The selection ofmixed-mode oscillations in a Hodgkin-Huxley model with multiple timescales.Chaos，2008，18（1）：015105

25 Nowacki J，Mazlan SH，Osinga H M，et al.The role of largeconductance Calcium-activated K+（BK）channels in shaping bursting oscillations of a somatotroph cellmodel. Physica D，2010，239（9）：485～493

26 Stern JV，Osinga H M，Lebeau A，et al.Resetting behavior in a model of bursting in secretory pituitary cells：Distinguishing plateaus from pseudo-plateaus.Bulletin of Mathematical Biology，2008，70（1）：68～88

27 Vo T，Bertram R，Tabak J，et al.Mixed-mode oscillations as amechanism for pseudo-plateau bursting.Journal of Computational Neuroscience，2010，28（3）：443～458

28 Krupa M，Popovic N，Kopell N，etal.Mixed-mode oscillations in a three time-scale model for the dopaminergic neuron.Chaos，2008，18（1）：015106

29 Medvedev G S，Cisternas JE.Multimodal regimes in a compartmentalmodel of the dopamine neuron.Physica D，2004，194（3-4）：333～356

30 Erisir A，Lau D，Rudy B，et al.Function of specific K+channels in sustained highfrequency firing of fast-spiking interneurons.Journal of Neurophysiology，1999，82（5）：2476～2489

31 Ermentrout B，Wechselberger M.Canards，clusters and synchronization in a weakly coupled interneuron model. SIAM Journal on Applied Dynamical Systems，2009，8（1）：253～278

32 Del Negro C A，Wilson CG，Butera R J，etal.Periodicity，mixedmode oscillations，and quasiperiodicity in a rhythm-generating neural network.Biophysical Journal，2002，82（1）：206～214

33 Lampl I，Yarom Y.Subthreshold oscillations of themembrane potential：A functional synchronizing and timing device.Journal of Neurophysiology，1993，70（5）：2181～2186

34 Giocomo L M，Zilli E A，Franscen E，et al.Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing.Science，2007，315（5819）：1719～1722

35 Desroches M，Guckenheimer J，Krauskopf B，et al. Mixed-mode oscillations with multiple time scales.SIAM Reviews，2012，54（2）：211～288

36 Rotstein H G.Mixed-mode oscillations in single neurons. Encyclopedia of Computational Neuroscience，2014，2（12）：1～9

37 Wang X J.Pacemaker neurons for the theta rhythm and their synchronization in the septohippocampal reciprocal loop.Journal of Neurophysiology，2002，87（2）：889～900

38 Muratov C B，Vanden-Eijnden E.Noise-induced mixedmode oscillations in a relaxation oscillator near the onset of a limit cycle.Chaos，2008，18（1）：387～416

39 Kuske R，Borowski P.Survival of subthreshold oscillations：the interplay of noise，bifurcation structure，and return mechanism.Discrete and Continuous Dynamical Systems，2009，2（4）：873～895

40 Brøns M，Kaper T J，Rotstein H G.Introduction to focus issue：mixed mode oscillations：experiment，computation，and analysis.Chaos：An Interdisciplinary Journal of Nonlinear Science，2008，18（1）：174～188

41 Hudson JL，Hart M，Marinko D.An experimental study ofmultiple peak periodic and nonperiodic oscillations in the Belousov-Zhabotinskii reaction.Journal of Chemical Physics，1979，71（4）：1601～1606

42 BakešD，SchreiberováL，Schreiber I，etal.Mixedmode oscillations in a homogeneous pH-oscillatory chemical reaction system.Chaos，2008，18（1）：015102

43 Baba N，Krischer K.Mixed-mode oscillations and cluster patterns in an electrochemical relaxation oscillator under galvanostatic control.Chaos，2008，18（1）：387～416

44 Higuera M，Porter J，Knobloch E.Faraday waves，streaming flow，and relaxation oscillations in nearly circular containers.Chaos，2008，18（1）：015104

45 Barkley D.Slow manifolds and mixed-mode oscillations in the Belousov-Zhabotinskii reaction.Journal of Physical Chemistry，1988，89（9）：5547～5559

46 Showalter K，Noyes R M，Barli K.A modified oregonator model exhibiting complicated limit cycle behaviour in aflow system.Journal of Physical Chemistry，1978，69（6）：2514～2524

47 Shilnikov L P.A case of the existence of a denumerable set of periodic motions.Soviet mathematics-Doklady，1965，6：163～166

48 Bronnikova T V，Schaffer W M，Olsen L F.Nonlinear dynamics of the peroxidase-oxidase reaction.I.Bistability and bursting oscillations at low enzyme concentrations. Journal of Physical Chemistry B，2001，105（1）：310～321

49 Krupa M，Popovic N，Kopell N，et al.Mixed-mode oscillations in a three time-scale model for the dopaminergic neuron.Chaos，2008，18（1）：015106

50 Desroches M，Krauskopf B，Osinga H M.Mixed-mode oscillations and slow manifolds in the self-coupled FitzHugh-Nagumo system.Chaos，2008，18（1）：015107

51 Arnold V I.Encyclopedia ofmathematical sciences：Dynamical systems V.Berlin/New York：Springer-Verlag，1994

52 Fenichel N.Geometric singular perturbation theory for ordinary differential equations.Journal of Differential Equations，1979，31（1）：53～98

53 Jones CK R T.Geometric singular perturbation theory，in Dynamical systems.Berlin/New York：Springer-Verlag，1995

54 Kaper T J.An introduction to geometric methods and dynamical systems theory for singular perturbation problems. analyzing multiscale phenomena using singular perturbation methods.Proceedings of Symposiain Applied Mathematics，1999，56：85～131

55 Tikhonov A N，Vasil′eva A B，Sveshnikov A G.Differential equations.Springer Series in Soviet Mathematics. Berlin/New York：Springer-Verlag，1985

56 Eckhaus W.Relaxation oscillations including a standard chase on french ducks.Lecture Notes in Mathematics，1983，985：449～494

57 Kevorkian J，Cole JD.Multiple scale and singular perturbation methods.Berlin/New York：Springer-Verlag，1996

58 BenoîtÉ.Enlacements de canards.Comptes Rendus de l′Académie des Sciences-Series I-Mathematics，1985，300（8）：225～230

59 Diener F，Diener M.Nonstandard analysis in practice. Berlin/New York：Springer-Verlag，1995

60 Desroches M，Guckenheimer F，Krauskopf J，et al. Mixed-mode oscillations with multiple time scales.SIAM Review，2010，54（2）：211～288

61 Wechselberger M，Mitry J，Rinzel J.Canard theory and excitability，nonautonomous dynamical systems in the life sciences.Lecture Notes in Mathematics，2013，2102：89～132

62 Eckhaus W.Relaxation oscillations including a standard chase on French ducks，Asymptotic Analysis II.Lecture Notes in Mathematics，1983，985：449～494

63 Dumortier F，Roussarie R.Canard cycles and centermanifolds.Memoirs of the American Mathematical Society，1996，121（577）：100

64 Krupa M，Szmolyan P.Relaxation oscillation and canard explosion.Journal of Differential Equations，2001，174（2）：312～368

65 Szmolyan P，Wechselberger M.Canards in R3.Journalof Differential Equations，2001，177（2）：419～453

66 Rinzel J，Ermentrout G B.Analysis of neural excitability and oscillations.In：Koch C，Segev I ed.Methods in Neural Modeling，second edition.Cambridge，Massachusetts：MIT Press，1998：251～292

67 Barnes B，Grimshaw R.Numerical studies of the periodically forced Bonhoeffer van der pol system.International Journal of Bifurcation and Chaos，2011，185（7）：2653～2689

68 Wechselberger M.Existence and bifurcation of canards in R3in the case of a folded node.SIAM Journal on Applied Dynamical Systems，2005，4（1）：101～139

69 Guckenheimer J.Return maps of folded nodes and folded saddle-nodes.Chaos，2008，18（1）：015108

70 Guckenheimer J.Singular hopf bifurcation in systemswith two slow variables.SIAM Journal on Applied Dynamical Systems，2008，7（7）：1355～1377

71 Krupa M，Wechselberger M.Local analysis near a folded saddle-node singularity.Journal of Differential Equations，2010，248（12）：2841～2888

72 Brøns M，Krupa M，Wechselberger M.Mixedmode oscillations due to the generalized canard phenomenon.Fields Institute Communications，2006，49（1）：39～63

73 Baer SM，Erneux T.Singular hopf bifurcation to relaxation oscillations.SIAM Journal on Applied Mathematics，1986，46（5）：721～739

74 Baer SM，Erneux T.Singular hopf bifurcation to relaxation oscillations II.SIAM Journal on Applied Mathematics，1992，52（6）：1651～1664

75 Braaksma B.Singular hopf bifurcation in systemswith fast and slow variables.Journal of Nonlinear Science and Ap-plications，1998，8（5）：457～490

76 Brøns M，Desroches M，Krupa M.Mixed-mode oscillations due to a singular hopf bifurcation in a forest pest model.Mathematical Population Studies，2015，22（2）：71～79

77 Alonso A，Klink R.Differential electroresponsiveness of stellate and pyramidal-like cells ofmedial entorhinal cortex layer II.Neutophysiol，1993，7（1）：128～143

78 Boyle D L.Spinal adenosine receptor activation inhibits inammation and jointed struction in rat adjuvant-induced arthritis.Arthritis Rheum，2002，46（11）：3076～3082

79 Alonso A，Llincas R.Subthreshold Na+-dependent theta like rhythmicity in stellate cells of entorhinal cortex layer II.Nature，1989，342（6246）：175～177

80 Dickson C T，Magistretti J，Shalinsky M H，et al.Properties and role of Ih in the pacing of subthreshold oscillation in entorhinal cortex layer II neurons.Journal of Neurophysiology，2000，83（5）：2562～2579

81 Leung L S，Yim C Y.Intrinsicmembrane potential oscillations in hippocampal neurons in vitro.Brain Research，1991，553（2）：261～274

82 Schmitz D，Gloveli T，Behr J，et al.Subthreshold membrane potentialoscillations in neurons of deep layers of the entorhinal cortex.Neuron，1998，85（4）：999～1004

83 Fernandez R，White JA.Artificial synaptic conductances reduce subthreshold oscillations and periodic firing in stellate cells of the entorhinal cortex.Journal of Neuroscience，2008，28（14）：3790～3803

84 Yoshida M，Alonso A.Cell-type-specificmodulation of intrinsic firing properties and subthreshold membrane oscillations by the M（Kv7）-currents in neurons of the entorhinal cortex.Journal of Neurophysiology，2007，98（5）：2779～2994.

85 Smith J C，Ellenberger H H，Ballanyi K，et al.Pre-Bötzinger complex：a brain stemreg ion thatmay generate respiratory rhythm inmammals.Science，1991，254：726～729

86 于海，陈予恕.高维非线性动力学系统降维方法的若干进展.力学进展，2009，39（2）：154～164（Yu H，Chen Y S.Recent developments in dimension reduction methods for high dimension dynamical systems.Advances in Mechanics，2009，39（2）：154～164（in Chiniese） ）

RESEARCH DEVELOPMENT ON DYNAM ICSOF M IXED-MODE OSCILLATIONS IN NEURONAL MODELS*

Lu Bo Liu Shenquan†Liu Xuanliang
（School of Mathematics，South China University of Technology，Guangzhou 510640，China）

Mixed-mode oscillations（MMOs）are a type of complex oscillation mode produced in dynamical systems.They arewidespread in nature.Mixed-mode oscillations aremade up of a series of small amplitude oscillations and large amplitude of the oscillations，and these two types of oscillations appear alternately.Mixed-mode oscillations in the neuronal system are introduced in this research.The effect of geometric singular perturbation theory on the generatingmechanism ofmixed mode oscillations in dynamic systems ismainly analyzed，and the research on dynamics ofmixed-mode oscillations in the Pre-BötC neural network，stellate cells of entorhinal cortex neurons，pituitary cells and gland cells is also introduced.Additionally，the investigation on mixed-mode oscillations of other neuronalmodels are briefly presented.All the works will provide a good foundation on further research on mixed mode oscillations of neuronalmodels in the future.

neuronalmodel， mixed mode oscillations， geometric singular perturbation theory， canard solution， relaxation oscillation

10.6052/1672-6553-2016-019

2015-12-11收到第1稿，2016-02-25收到修改稿.

*国家自然科学基金资助项目（11172103）

†通讯作者E-mail：mashqliu＠scut.edu.cn

Received 11 December 2015，revised 25 February 2016.

*The project supported by the National Natural Science Foundation of China（11172103）

†Corresponding author E-mail：mashqliu＠scut.edu.cn