刘金建 蔡改改 谢锋 黄伟国 李成

（苏州大学城市轨道交通学院，苏州 215131）

轴向运动功能梯度粘弹性梁横向振动的稳定性分析*

刘金建 蔡改改 谢锋 黄伟国 李成†

（苏州大学城市轨道交通学院，苏州 215131）

基于Euler梁理论研究了轴向运动功能梯度粘弹性梁横向振动的稳定性问题.基于问题的数学模型和控制方程，利用微分求积法求得了轴向匀速运动功能梯度粘弹性梁亚临界区域内横向振动的复频率，分析其随着轴向运动速度、材料梯度指数等参数的变化情况，探讨上述参数对超临界区域失稳形式的影响.然后应用多尺度法结合边界条件分析了轴向速度带有周期扰动成分的变速运动功能梯度粘弹性梁的失稳问题，重点讨论了当速度扰动频率为固有频率二倍或者为两固有频率之和/差时所发生的次谐波共振及组合共振所导致的失稳.数值算例表明，随着梯度指数的增大，匀速运动功能梯度粘弹性梁的临界发散速度、耦合速度以及变速运动功能梯度粘弹性梁的稳定区域减小，且粘弹性系数的影响逐渐变弱，同等条件下，轴向运动功能梯度粘弹性固支梁比简支梁更为稳定.

轴向运动， 功能梯度粘弹性梁， 稳定性， 次谐波共振， 组合共振

引言

轴向运动梁是一种重要的工程构件，在动力传送带、磁带、纺织纤维、带锯、空中缆车索道、升降机缆绳等工程系统中应用广泛.轴向运动梁的横向振动会带来某些影响，比如带锯的横向振动会影响到切割质量，其稳定性值得关注.关于轴向运动梁的动力学与控制问题已经得到了广泛的研究［1-8］.比如，Öz等［1］基于多尺度法研究了轴向变速运动梁的振动及稳定性.罗炳华等［5］建立了轴向运动梁受移动载荷作用的有限元模型，并提出了描述运动梁节点约束状态的节点生死方法.Yang和Zhang［8］考虑纵横向耦合情况下轴向运动梁的非线性振动，应用多尺度法得到了系统在内外共振时的稳态响应.

随着科技的进步，工程结构中很多关键部件要求材料性能具有可设计性，以适应其特殊的工作和受载环境.功能梯度材料［9-16］就是其中之一，它通常由两种不同性能的材料组成，且组织成分和显微结构均呈连续性变化，这有利于集两种材料的优良特性于一体.这方面，Yang等［9］基于二维弹性理论研究了处于弹性地基上各向异性功能梯度梁的自由振动.Ansari等［12］基于应变梯度Timoshenko梁理论研究了功能梯度微梁的自由振动，并与经典理论、修正的偶应力理论及应变梯度理论的结果进行了对比.尹硕辉等［14］基于一阶剪切变形板理论，建立了分析功能梯度板自由振动问题的非均匀有理B样条等几何有限元格式，并采用等几何有限元法讨论了各个参数对功能梯度板的动态响应的影响. Aghazadeh等［16］基于修正的偶应力理论分析了功能梯度小尺度梁的自由振动，其中分别考虑了Euler、Timoshenko和三阶剪切变形梁模型.

功能梯度材料已经被应用到航空航天等大型工程结构中，比如航天飞机燃烧室内壁等，功能梯度材料的耐热隔热强韧性等特点解决了航天材料的热应力缓和问题，因此研究轴向运动功能梯度材料梁很有必要.赵凤群等［17］基于Timoshenko梁模型应用微分求积法得到了简支功能梯度梁的特征方程及复频率与轴向运动速度的关系，并且分析了梁随轴向速度变化的失稳形式，以及梯度指数、长高比对梁的动力稳定性影响.李成等［18］研究了轴向运动功能梯度弹性梁的梯度指数、轴向速度、初始应力等对振动频率、模态函数等的影响.然而，关于轴向变速运动功能梯度粘弹性梁的稳定性分析目前还不多见.本文以轴向运动Euler梁模型为切入点，并假设功能梯度梁结构及其性质沿厚度方向呈现幂函数连续变化.考虑到Euler梁模型厚度远小于跨度，弯曲变形占主导地位，因此可以忽略剪切变形的影响.在匀速条件下，利用微分求积法分析了超临界区域轴向运动功能梯度粘弹性梁的动态特性及其失稳形式，详细讨论了轴向运动速度和梯度指数对功能梯度粘弹性梁的横向振动特性以及失稳形式的影响.对于轴向变速运动功能梯度粘弹性梁，采用多尺度法研究了前三阶和型组合共振及其次谐波共振，并进一步讨论若干重要参数对稳定性的影响.

1 轴向运动功能梯度Euler梁模型及其稳定性分析

考虑长度为L，横截面宽为b，厚为h，两端受初始轴向应力σ0作用的轴向运动功能梯度粘弹性梁，其控制方程为［2］

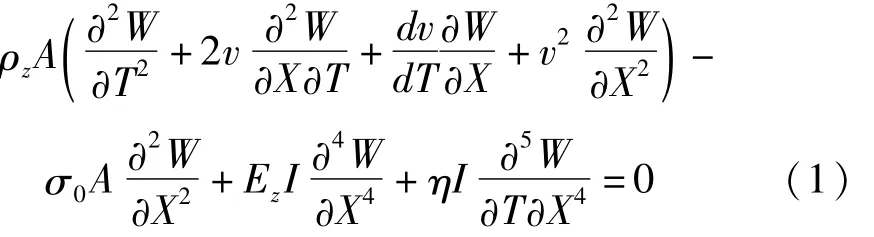
其中，W为横向位移，T为时间，v为轴向速度，X为梁的轴向坐标，η为粘弹性系数，，Z为厚度方向坐标.假设功能梯度材料弹性模量EZ和密度ρZ沿厚度方向按幂函数规律变化，即

1.1 匀速运动时的稳定性分析

方程（6）应用复模态法可以求得亚临界区域内轴向运动功能梯度梁横向振动频率，但对于确定超临界区域的失稳原因，复模态法却难以胜任，因此对超临界区域内的失稳形式分析，本文采用了微分求积法.

选取非均匀网点共N个，则网点的坐标为

方程（16）有非零解的充分必要条件是系数矩阵的行列式为零.对于边界条件为两端固支的情况，将利用式（11）和式（13）同样可推得式（16）的形式，其中仅M，G，K有所不同.

1.2 变速运动时的参数振动及稳定性分析

利用式（7）可以分析轴向变速运动功能梯度粘弹性梁的参数稳定性，为表示脉动频率ω在ωm+ωn附近变化，引入调谐参数σ，即

其中，符号上的点和撇分别表示对时间T1和x求导，NST表示不会给解带来永年项部分.若要使得解不存在永年项，则可解性条件要求非齐次微分方程（19）的非齐次部分与其伴随方程的齐次解正交，即有

其中，φj、φk分别为第j阶和第k阶模态函数，且由方程（6）的模态函数所决定，与轴向速度的脉动量无关.

将（20）式转换为自治方程，考虑其自治方程的非零解，得稳定性判断条件

其中λ是待定复数.如果λ有正实部解，则系统不稳定，如果λ全部为负实部，则系统稳定.经过数值计算分析知合型共振的失稳区域为

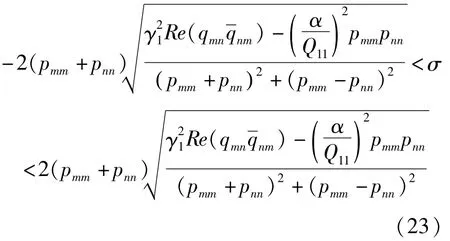
进一步地，当轴向速度简谐脉动频率ω接近两阶固有频率之差时，就会发生差型组合参数共振.同样用调谐参数σ来表示ω偏离ωm-ωn的程度，则此时ω为

类比和型组合参数共振分析过程知，式（23）也是系统差型组合共振稳定性边界条件，只是其系数pkk和qkj不同于和型组合.

最后，当轴向速度简谐脉动频率ω接近n阶固有频率ωn的2倍时，就会发生次谐波共振.此时，调谐参数σ用来表示ω偏离2ωn的程度，即有

令（23）式中m＝n，即得n阶次谐波共振的稳定性边界条件为

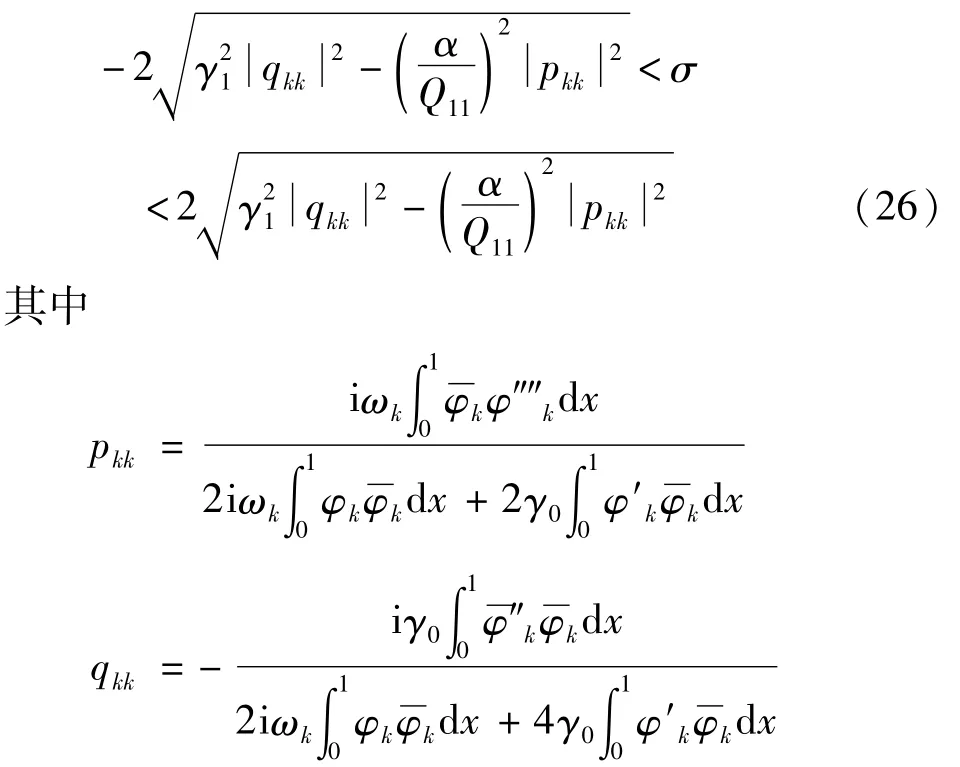
2 算例分析与讨论

为了具体描述横向振动稳定性受功能梯度指数的影响，对轴向匀速、变速运动功能梯度粘弹性梁分别提供了两个算例，算例中梁的参数如下：Ec＝390GPa，ρc＝3960kg/m3，Em＝210GPa，ρm＝7800kg/m3，则ηE＝Ec/Em＝1.86，ηρ＝Ec/Em＝0.51.

2.1 匀速运动时的稳定性

本例取δ＝10-6，N＝19，k分别为0.01，1，100，研究轴向运动功能梯度梁横向振动的前三阶复频率随轴向运动速度的变化.虽然复模态法能够准确地求得亚临界区域内轴向运动功能梯度梁的横向振动频率随着各个参数的变化，但对于超临界区域尤其是发散失稳现象及耦合颤振现象发生区，复模态法很难确定各阶频率的具体取值.因此本文应用微分求积法重点探讨超临界区域功能梯度指数对失稳形式的影响.

为验证本文计算方法的有效性，表1给出了亚临界区域内一阶频率复模态结果与微分求积结果的对比.不难发现亚临界区域轴向运动功能梯度梁的横向振动频率随着梯度指数的增大而减小，亦可看出微分求积结果与复模态结果十分吻合.

表1 一阶频率微分求积结果与复模态结果的对比Table 1 Comparisonof the results obtained from the differential quadrature and complexmodalmethods for the first order natural frequency

图1～3反映了功能梯度简支梁复频率随着k、γ0的变化情况.

从图1可见，当k＝0.01时，频率的虚部（固有频率）在γ0＝2.6处第一阶模态出现发散失稳，即临界发散速度.复频率虚部的发散在实部上相应的表现形式为实频率从零开始向正负两个方向对称发散，即出现正负两个值，且其绝对值先增大后减小.图2给出了k＝1的情况，当1.9＜γ0＜3.8时，此时第一阶模态处于发散失稳状态，当3.8＜γ0＜3.9时，第一阶频率迅速增大，此时一阶频率处于再稳定状态，当γ0＞3.9时，第一、二阶频率耦合在一起，即此时第一、二阶频率发生耦合颤振失稳.当k＝100时的结果如图3所示，第一阶模态在γ0＝1.5处即出现发散失稳，当2.9＜γ0＜4时，为第一、二阶模态耦合颤振区域，与图1、2不同的是当γ0＝4.4的时候将发生第二、三阶耦合颤振失稳.总之，随着材料梯度指数和轴向运动速度的增大，轴向运动功能梯度梁横向振动的临界速度和失稳形式表现出较强的材料敏感性及速度依赖性.

类似地，两端固支的情形如图4～6所示.在其他条件相同的情况下，轴向运动功能梯度固支梁的横向振动前三阶复频率变化规律与两端简支时相似.不同的是，两端固支的稳定区域大于简支时的稳定区域，且各阶固有频率的发散速度均大于两端简支时的情形，这也表明轴向运动功能梯度固支梁比简支边界条件下更稳定.

图1 两端简支前三阶复频率虚部/实部随轴向速度的变化曲线（k＝0.01）Fig.1 First three order complex frequencies axial speed relationships for H-H FGM beam（k＝0.01）

图2 两端简支前三阶复频率虚部/实部随轴向速度的变化曲线（k＝1）Fig.2 First three order complex frequencies the axial speed relationship for H-H FGM beam（k＝1）

图3 两端简支前三阶复频率虚部/实部随轴向速度的变化曲线（k＝100）Fig.3 First three order complex frequencies the axial speed relationship for H-H FGM beam（k＝100）

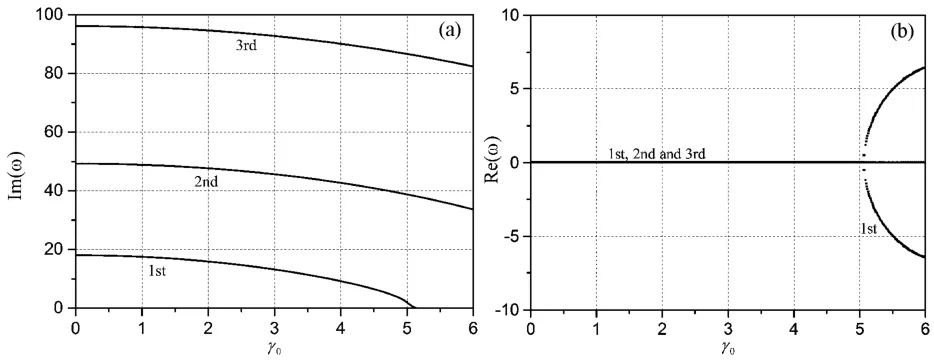
图4 两端固支前三阶复频率虚部/实部随轴向速度的变化曲线（k＝0.01）Fig.4 First three order complex frequencies the axial speed relationship for C-C FGM beam（k＝0.01）

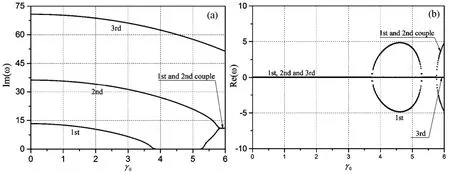
图5 两端固支前三阶复频率虚部/实部随轴向速度的变化曲线（k＝1）Fig.5 First three order complex frequencies the axial speed relationship for C-C FGM beam（k＝1）

图6 两端固支前三阶复频率虚部/实部随轴向速度的变化曲线（k＝100）Fig.6 First three order complex frequencies the axial speed relationship for C-C FGM beam（k＝100）

2.2 变速运动时的稳定性

对于轴向运动功能梯度粘弹性梁的和型组合共振、差型组合共振和次谐波共振的稳定性边界来说，稳定性边界方程中的系数qjk，pkk可由方程（6）的模态函数和固有频率确定.因此，轴向运动功能梯度粘弹性梁参数共振的不稳定性区域为

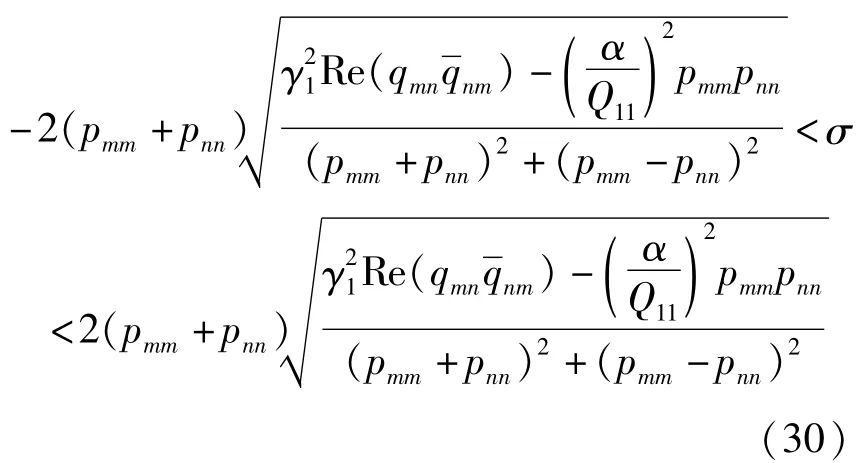
为讨论各主要参数对轴向变速运动功能梯度粘弹性梁的稳定性的影响，选取α＝0.0001，γ0＝1.图7～9分别给出了当k＝0.01、1、100时，两端简支梁第1、2阶组合共振，第1、3阶组合共振，第2、3阶组合共振在σ-γ1平面上的失稳区域.

图7 两端简支轴向运动功能梯度梁第1和第2阶组合共振失稳区域Fig.7 Unstable regions for summation resonances of the 1stand 2ndmodes（H-H）

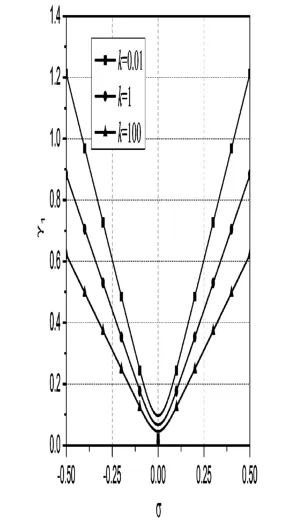
图8 两端简支轴向运动功能梯度梁第1和第3阶组合共振失稳区域Fig.8 Unstable regions for summation resonances of the 1stand 3rdmodes（H-H）

由图7～9可见，增大梯度指数将使得失稳区域增大，即在给定σ时，增大梯度指数将导致失稳脉动振幅的γ1阀值减小，反之当给定γ1时，增大梯度指数将使得失稳的频率范围增大.图10～12分别作出了当k＝0.01，1，100时，两端简支梁前三阶次谐波共振的失稳区域.前三阶次谐波共振随梯度指数的变化表现出相似的规律，即增大梯度指数，失稳范围变宽.对比图7～12可知，k越小，粘弹性系数对稳定性的影响越明显.

图9 两端简支轴向运动功能梯度梁第2和第3阶组共振失稳区域Fig.9 Unstable regions for summation resonances of the 2ndand 3rdmodes（H-H）

图10 两端简支轴向运动功能梯度梁第1阶次谐波合共振失稳区域Fig.10 Unstable regions for sub-harmonic resonances of the 1stmode（H-H）

图11 两端简支轴向运动功能梯度梁第2阶次谐波共振失稳区域Fig.11 Unstable regions for sub-harmonic resonances of the 2ndmode（H-H）

两端固支梁第1、2阶，1、3阶及2、3阶组合共振随材料梯度指数变化的情况分别由图13～15给出.由图13～15可知，随着梯度指数的增大失稳范围变宽.此外，两端固支梁前三阶次谐波共振稳定区域随功能梯度指数的变化如图16～18所示，可见前三阶次谐波共振随梯度指数的变化规律一致，即随着梯度指数增大失稳范围变宽.进一步对比图16～18可见，在其他参数给定的条件下，随着k的增大，粘弹性系数对参数稳定性的影响逐渐削弱.

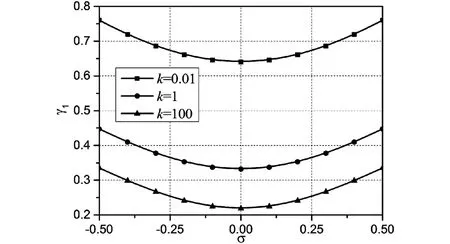
图12 两端简支轴向运动功能梯度梁第3阶次谐波共振失稳区域Fig.12 Unstable regions for sub-harmonic resonances of the 3rdmode（H-H）

图13 两端固支轴向运动功能梯度梁第1和第2阶组合共振失稳区域Fig.13 Unstable regions for summation resonances of the 1stand 2ndmodes（C-C）

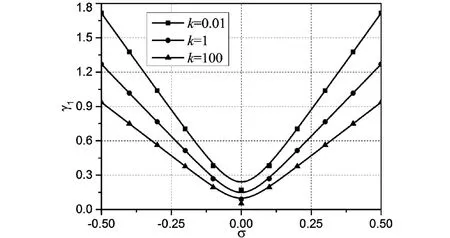
图14 两端固支轴向运动功能梯度梁第1和第3阶组合共振失稳区域Fig.14 Unstable regions for summation resonances of the 1stand 3rdmodes（C-C）

图15 两端固支轴向运动功能梯度梁第2和第3阶组合共振失稳区域Fig.15 Unstable regions for summation resonances of the 2ndand 3rdmodes（C-C）

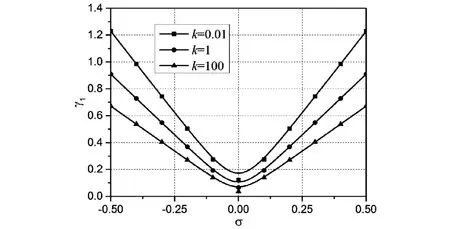
图16 两端固支轴向运动功能梯度梁第1阶次谐波共振失稳区域Fig.16 Unstable regions for sub-harmonic resonances of 1stmode（C-C）

图17 两端固支轴向运动功能梯度梁第2阶次谐波共振失稳区域Fig.17 Unstable regions for sub-harmonic resonances of the 2ndmode（C-C）

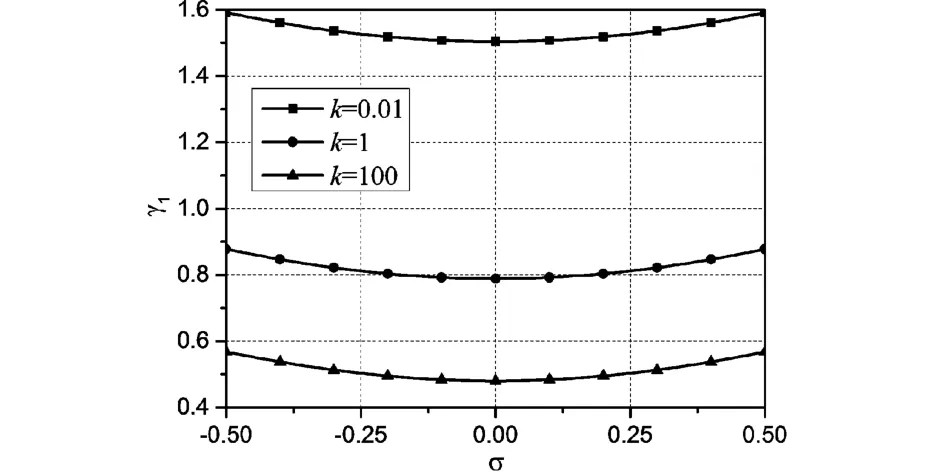
图18 两端固支轴向运动功能梯度梁第3阶次谐波共振失稳区域Fig.18 Unstable regions for sub-harmonic resonances of 3rdmode（C-C）

3 结论

针对轴向运动功能梯度粘弹性梁所存在的轴向速度与横向振动的相互耦合，研究了其运动稳定性问题.利用微分求积法分析了轴向匀速运动功能梯度梁的动态特性及其失稳形式.随着轴向运动速度的增大，功能梯度梁横向振动的前三阶复频率的虚部逐渐减小，当速度增大到一定值时复频率的虚部开始出现发散失稳和耦合颤振失稳.随着材料梯度指数的增大，轴向运动功能梯度梁的临界发散速度和耦合速度明显减小.当材料梯度指数增大到一定值时，材料更接近金属材料，此时随着梯度指数的增大复频率不再显著变化.

通过多尺度法分析给出了变速运动功能梯度粘弹性梁的六种共振失稳区域，即前三阶次谐波共振及其相互组合共振的失稳区域.研究了梯度指数对失稳范围的影响.结果表明，六种共振失稳区域随着梯度指数的增大而增大，且随着梯度指数的减小，粘弹性对参数稳定性的影响更为明显.研究结果对理解轴向匀速及变速运动功能梯度类梁结构的稳定性具有指导意义，并为该类构件的工程应用提供参考.

1 Öz H R，Pakdemirli M，BoyacıH.Non-linear vibrations and stability ofan axiallymoving beam with time-dependent velocity.International Journal of Non-Linear Mechanics，2001，36（1）：107～115

2 Chen LQ，Yang X D.Stability in parametric resonance of axially moving viscoelastic beams with time-dependent speed.Journalof Sound and Vibration，2005，284（3）：879～891

3 Ghayesh M H，Yourdkhani M，Balar S，Reid T.Vibrations and stability ofaxially traveling laminated beams.Applied Mathematics and Computation，2010，217（2）：545～556

4 Ding H，Chen L Q.Galerkin methods for natural frequencies of high-speed axiallymoving beams.Journal of Sound and Vibration，2010，329（17）：3484～3494

5 罗炳华，高跃飞，刘荣华等.轴向运动梁受移动载荷作用的横向动力响应.振动与冲击，2011，30（12）：59～63（Luo BH，Gao Y F，Liu R H，etal.A study on lateral dynamic response of an axially moving beam under a moving load.Journal of Vibration and Shock，2011，30（12）：59～63（in Chinese））

6 胡超荣，丁虎，陈立群.混杂边界轴向运动Timoshenko梁固有频率数值解.振动与冲击，2011，30（7）：245～249（Hu C R，Ding H，Chen L Q.Natural frequency numerical solution of an axiallymoving Timoshenko beam with hybrid boundary.Journal of Vibration and Shock，2011，30（7）：245～249（in Chinese））

7 Wang L，Hu Z，Zhong Z.Non-linear dynamical analysis for an axiallymoving beam with finite deformation.International Journal of Non-Linear Mechanics，2013，54（3）：5～21

8 Yang X D，ZhangW.Nonlinear dynamics of axiallymoving beam with coupled longitudinal-transversal vibrations.Nonlinear Dynamics，2014，78（4）：2547～2556

9 Ying J，LüC F，Chen W Q.Two-dimensionalelasticity solutions for functionally graded beams resting on elastic foundations.Composite Structures，2008，84（3）：209～219

10 Li X F.A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams.Journal of Sound and Vibration，2008，318（4）：1210～1229

11吴晓，罗佑新.用Timoshenko梁修正理论研究功能梯度材料梁的动力响应.振动与冲击，2011，30（10）：245～248（Wu X，Luo Y X.Dynamic responses of a beam with functionally graded materials with Timoshenko beam correction theory.Journal of Vibration and Shock，2011，30（10）：245～248（in Chinese））

12 Ansari R，GholamiR，Sahmani S.Free Vibration analysis of size-dependent functionally graded microbeams based on the strain gradient Timoshenko beam theory.Composite Structures，2011，94（1）：221～228

13 Ke L L，Wang Y S，Yang J，et al.Nonlinear free vibration of size-dependent functionally graded microbeams.International Journal of Engineering Science，2012，50（1）：256～267

14尹硕辉，余天堂，刘鹏.基于等几何有限元法的功能梯度板自由振动分析.振动与冲击，2013，32（24）：180～186（Yin SH，Yu T T，Liu P.Free vibration analysis of functionally graded plates using isogeometric finite element method.Journal of Vibration and Shock，2013，32（24）：180～186（in Chinese））

15 Tang A Y，Wu JX，Li X F，etal.Exact frequency equations of free vibration of exponentially non-uniform functionally graded Timoshenko beams.International Journal of Mechanical Sciences，2014，89：1～11

16 Aghazadeh R，Cigeroglu E，Dag S.Static and free vibration analyses of small-scale functionally graded beams possessing a variable length scale parameter using different beam theories.European Journal of Mechanics-A/Solids，2014，46（1）：1～11

17赵凤群，王忠民，路小平.轴向运动功能梯度Timoshenko梁稳定性分析.振动与冲击，2014，33（2）：14～19（Zhao F Q，Wang Z M，Lu X P.Stability analysis of axially moving Timoshenko beam made of functionally graded material.Journal of Vibration and Shock，2014，33（2）：14～19（in Chinese））

18李成，随岁寒，杨昌锦.受初应力作用的轴向运动功能梯度梁的动力学分析.工程力学，2015，32（10）：226～232（Li C，SuiSH，Yang C J.Dynamic analysis ofaxially moving functionally graded beams subjected to initial stress.Engineering Mechanics，2015，32（10）：226～232（in Chinese））

19 Sui SH，Chen L，Li C，Liu X P.Transverse vibration of axially moving functionally graded materials based on Timoshenko beam theory.Mathematical Problems in Engineering，2015

20张国策，丁虎，陈立群.复模态分析超临界轴向运动梁横向非线性振动.动力学与控制学报，2015，13（4）：283～287（Zhang G C，Ding H，Chen L Q.Complex modal analysis of transversally non-linear vibration for supercritically axiallymoving beams.Journal of Dynamicsand Control，2015，13（4）：283～287（in Chinese） ）

STABILITY ANALYSISON TRANSVERSE VIBRATION OF AXIALLY MOVING FUNCTIONALLY GRADED VISCOELASTIC BEAMS*

Liu Jinjian Cai Gaigai Xie Feng Huang Weiguo Li Cheng†
（School of Urban Rail Transportation，Soochow University，Suzhou 215131，China）

The stability of the transverse vibration of an axially moving functionally graded viscoelastic beam（FGVB）is studied based on the Euler beam theory.The complex frequencies of FGVB are firstly investigated by the differential quadraturemethod，where themain parameters such as axial speed and gradient index are considered.The effects of the axial speed and gradient index on the vibration characteristics and instable forms in supercritical region are also examined.Subsequently，the instability behaviors of FGVB with periodic perturbational velocity are addressed using the method ofmultiple scales and specific boundary conditions.The discussion is then mainly focused on the instable regions caused by summation resonance and sub-harmonic resonance，respectively，where the resonance occurs when the harmonic frequency approaches the sum or difference of any two mode natural frequencies.It is shown that the critical divergence and flutter velocities of the uniformly moving beam，aswell as the stability regions of non-uniform lymoving beam decrease with the increase of gradient index，and the viscoelastic effect becomesweakerwith increasing gradient index.Moreover，the stability regions of axiallymoving FGVB for fully clamped boundary condition are larger than those for the simply supported case.

axialmoving， functionally graded viscoelastic beam， stability， sub-harmonic resonance，summation resonance

10.6052/1672-6553-2016-013

2016-01-05收到第1稿，2016-01-21收到修改稿.

*国家自然科学基金资助项目（51405320，51405321），江苏省自然科学基金（BK20140339，BK20130303），江苏省高校自然科学研究面上项目（14KJB460023），苏州市科技计划项目（SYG201537）

†通讯作者E-mail：licheng＠suda.edu.cn

Received 5 January 2016，revised 21 January 2016.

*The project supported by the National Natural Science Foundation of China（51405320，51405321），Natural Science Foundation of Jiangsu Province（BK20140339，BK20130303），Natural Science Foundation of the Jiangsu Higher Education Institutions of China（14KJB460023），and Natural Science Foundation of Suzhou（SYG201537）

†Corresponding author E-mail：licheng＠suda.edu.cn