李耀宗，范小宁

（太原科技大学 机械工程学院，太原 030024）

0 引言

桥式起重机，在起重运输行业中占有重要的地位，其主要由桥架、小车和电气部分三大部分构成，其中作为桥架主要组成部分的主梁，是整机的主要承载构件，一旦发生结构破坏，轻则造成重大财产损失，重则引起人员伤亡，因此必须保证其具有非常高的可靠性，即很小的失效概率。目前起重机金属结构设计计算中均采用许用应力法[1]，该方法通过设置某一固定的安全系数,在结构构件服役期间，截面上任何一点的应力值都不应大于给定的许用应力值，虽然许用应力法使用简单，但其无法充分考虑结构的载荷，材料性质，结构尺寸等的不确定性对其可靠性的影响，不能定量的描述可靠性的大小。

针对金属结构的概率可靠性计算方法，如直接蒙特卡洛模拟法[2,3]，尽管具有适应性强，对变量维数不敏感，且不需要事先知道失效域的任何信息等优点，但由于抽样数目过于庞大，导致其在模拟小失效概率时效率非常低下。其他缩减方差的数字模拟法，如重要抽样法[4,5]，分层抽样法等，尽管比直接蒙特卡洛抽样法在抽样次数上有所降低，但在计算大型复杂结构的小失效概率时其计算效率仍难以满足实际要求。

针对以上问题，本文介绍了一种能极大提高多维小失效概率问题计算效率的方法-子集模拟方法[6]，它的主要思想是通过选择合适的中间失效事件，进而可以将概率空间划分成一系列的子集，小的失效概率则采用一系列较大的中间失效事件条件概率的乘积来表示，该方法最早由Au和Beck于2001年提出，并在多个领域取得广泛而成功的应用。文献[7,8]将子集模拟法用于边坡可靠性分析中，且文献[8]解决了含相关非正态变量的边坡可靠性问题。文献[9,10]将子集模拟法用于结构的动力可靠度计算，并取得了可喜的研究成果, 可见其在求解小概率失效问题时的有效性和可行性, 因而成为当前进行结构可靠度研究的热点问题。鉴于此, 本文将子集模拟法引入到起重机金属结构的可靠度计算中，通过对简单数值算例和工程算例可靠度进行子集模拟，并与直接蒙特卡洛法计算结果进行对比，表明所提方法不受极限状态方程非线性程度的影响，可有效减少计算成本，具有较高的计算效率和精度。

1 子集模拟法

1.1 子集模拟法的基本原理

子集模拟法[6,11,12]的主要思想是通过选择合适的中间失效事件，将小概率问题转化为一系列较大条件概率的乘积。若结构的功能函数为Z(x)，失效域定义为F={x|Z(x)＞lim}，通过引入一系列的临界值t1＜t2＜...＜tm=lim，可以形成一系列具有包含关系的中间失效事件Fk，Fk={x|Z(x)＞tk},(k=1,2,...,m)，即F1⊃ F2⊃...⊃Fm=F ，且有。根据条件概率中乘法定理的定义，失效概率可以进一步表述为：

令P1=P(F1),Pj=P(Fj|Fj−1)(,j=2,3,...,m)

若m=4，Pj为0.1量级，则Pf可以达到10-4量级，在其他情况都相同的情况下，不管是从效率还是精度方面来说，数字模拟法计算0.1量级的失效概率，都比计算10-4量级更有优势。对于10-4量级的失效概率，若采用直接蒙特卡罗法，则需要100/Pf[13,14]即1000000次抽样才能达到需要的精度，若采用子集模拟法，则只需大概4×100/Pj次即4000次抽样就可以达到需要的精度，效率提高了99.6%。通过以上分析可知，子集模拟法可以把小的失效概率表示成一连串容易求解的相对较大的失效概率的乘积，采用数字模拟法则可以高效的求解相对较大的失效概率，从而显著提高小失效概率的计算效率。

1.2 条件样本点的 MCMC 模拟

式(2)中P1的估计值 Pˆ1可以通过直接蒙特卡罗方法获得，而 Pj, (j = 2,3,...,m)的估计值Pˆj则可以通过抽取条件样本点来进行计算。

子集模拟法的关键在于构造合适的马尔科夫链[6,15]，并通过马尔科夫链获得一系列的样本，随着马尔科夫链链长的不断扩展，链上样本相对应的工程系统响应值的概率分布会越来越接近响应的真实分布。马尔可夫链蒙特卡罗法中出现较早且目前应用较为广泛的方法是M-H算法[11,15]，该算法要求随机向量的各个分量相互独立[16]，此法通过在当前样本点附近的随机游动来得到下一点，进而可以构建出一条马尔科夫链，简称马氏链。设马氏链的当前状态点为x，x∈F，F为失效域，M-H算法的目的是得到下一个状态点y∈F，其具体操作过程如下：

1）选取具有对称性的建议分布函数p(y|x)[6,11]，因其对称性，有 p (y|x)= p(x|y)。从理论上讲, 建议分布函数p(y|x)可以随意选取，但实际应用中，算法效率会受到建议分布函数的影响。目前普遍认为建议分布函数的形式越接近目标函数分布[6,15]，则模拟的效果越好。实际应用中多取一维均匀分布或正态分布作为“建议分布函数”，本文选取一维均匀分布为建议分布函数，建议分布函数的标准差取为对应随机变量的标准差。

2）以当前样本点作为建议分布函数的中心，通过建议分布函数随机产生一点ζ，计算接受概率r=min(1 ,f(ζ)/f(x))，其中f为功能函数。以概率r接受ζ，即=ζ，以概率1-r拒绝ζ，即=x。具体可以此操作：从均匀分布[0,1]随机产生一个数字u，若u＜r，则=ζ，若u＞r，则=x。

第二步：接受或拒绝阶段

第三步：产生新的状态点

继续以新的y作为新的当前状态点，重复第一步和第二步，即可产生下一个新的状态点。重复一、二和三步，即可生成一条完整的马氏链。

以上过程仅为一维状态下产生马氏链的过程，在本文的研究背景下，各个设计变量是独立同分布的，所以在具有多个设计变量的情况下，只需将当前样本点的各个分量作为马氏链的起始状态点，分别对每个分量重复步骤一、二和三，即可产生一条多维状态下的马氏链。

1.3 中间失效事件的选择

中间失效事件[6,11]的选择在子集模拟过程中占据重要地位。一种情况下，如果中间失效事件非常多(m值很大)，即 tj, (j = 1,2,...,m)减小变慢，则相应的条件失效概率可以很大，用较少的条件样本点即可以模拟对应的条件失效概率，但总的样本点数将会增多；在另一种情况下，中间事件比较少，则相应的条件失效概率会很小，此时需要较多的条件样本点才能精确的模拟很小的条件失效概率，同样会导致总的抽样点数的增多。故目前中间失效事件的选择方法为：在模拟条件失效概率的样本点数Nj和中间失效事件的数量m上折衷[6]，即通过提前选定条件概率p0，根据实际需要自适应地进行分层，本文亦采用该法进行中间失效事件的选择。

1.4 子集模拟法的具体步骤

1）用直接蒙特卡罗模拟法产生N（本文中N=1000）个服从联合概率密度函数为fX(x)的相互独立的样本{:k= 1,2,...,N}。

3）从落在 Fj-1(j =2,3,...,m)域内的p0N个样本点出发，以每个样本点作为马氏链的种子，共产生p0N条马氏链，每条马氏链可产生(1-p0)/p0个新的样本点，p0N条马尔科夫链共产生(1-p0)/N个条件样本点，这(1-p0)/N个新产生的样本点与作为种子的p0N个样本点总数共为N，且它们均为服从密度函数 q (x| Fj-1)的条件样本点，即{,k = 1,2,...,N}。

4）与步骤（2）相似，用功能函数Z(x)计算这N个条件样本相应的系统响应值，{Z(),k=1,2,...,N;j=2,3,...,m}，同样对响应值按照由小到大的顺序排序，以第(1-p0)/N个值作为中间失效事 件 Fj={x|Z(X )＞tj}的 临 界 值tj， 同 时 得 到P（Fj|Fj-1)=p0。

5）重复步骤(3)和(4)，直到第(1-p0)/N个响应值的值大于lim，令tm=1im，自动分层至此结束。计算落入失效域F中的服从密度函数 q (x| Fm-1)的条件样本点的个数Nf，可得 P(Fm|Fm-1)=Nf/N。

2 算例分析

为证明所提方法的可行性和有效性，以下给出数值算例和工程算例，并将子集模拟法的计算结果与直接蒙特卡罗法进行对比。为研究方便假定算例中各随机变量之间相互独立，且均为正态分布（非正态分布的随机变量可通过Rosenblatt变换转换成正态分布[17]）。

2.1 数值算例

数值算例1

g(x1,x2,x3)=x31+2x2-5x3，界限值为5，其中x1～N(5,0.1)，x2～N(36,0.2)，x3～N(39,0.1)。

数值算例2

g(x1,x2,x3,x4)=x31+2.x22-2.x3.X4，界限值为0，其中x1～N(2,0,01)，x2～N(5,0.02)，x3～N(5,0.01)，x4～N(6,0.03)。

数值算例3

g(x1,x2,x3,x4,x5)=x51-x22/(x3.x4)-2.x25，界限值为-2，其中x1～N(3,0.003)，x2～N(15,0.02)，x3～N(2,0.01)，x4～N(10,0.5)，x5～N(11,0.01)。

三个数值算例的直接蒙特卡罗法与子集模拟法的计算结果如表1所示。

表1 数值算例计算结果

三个数值算例分析结果显示, 尽管直接蒙特卡罗法具有抽样量大，计算效率低下的缺点，但是由于其计算精度高，适应性强，通常将其计算结果作为精确值与其他计算方法进行对比。从表1的计算结果可见, 三个数值案例的子集模拟法与直接蒙特卡罗法的计算误差分别为8.3%，3.7%，4.3%，而子集模拟法的抽样次数分别仅为直接蒙特卡洛法的3%，0.05%，0.000009%，可以看出，在计算精度近似相同的情况下，与直接蒙特卡洛法相比，子集模拟法所需的抽样次数显著降低，从而提高了计算效率。

2.2 工程算例

已知某偏轨双梁桥式起重机，其性能参数为：额定起重量mQ=32t，小车质量mx=1t，吊具质量m0=1t，跨度25.5m，工作级别为A6。双梁桥式起重机的两根主梁对称布置，载荷通过小车车轮作用于主梁，两根主梁具有相同的的受力特征，以一根主梁进行分析即可。图1是主梁受力图，图2为主梁的截面图。满载小车位于主梁跨中是主梁最危险的工况，因此以满载小车位于主梁跨中时跨中的静刚度和跨中截面的第3个危险点的应力[18]建立功能函数如下：

静刚度功能函数：

许用挠度为L/800。

3点应力功能函数：

许用应力为175MPa。

式中：

以上各式中：x2,y2：主梁形心坐标；Ix,Iy：主梁惯性矩；I2：端梁惯性矩；L：主梁跨度；K：小车轨距；B0：大车轴距；B：端梁全长；b：小车轮距；d1：大车运行机构与大车轨道距离；d2：司机室与大车轨道距离；mg：小车轨道质量；ml：栏杆质量；mj：大车运行机构质量；ms：司机室质量。

图1 主梁受力图

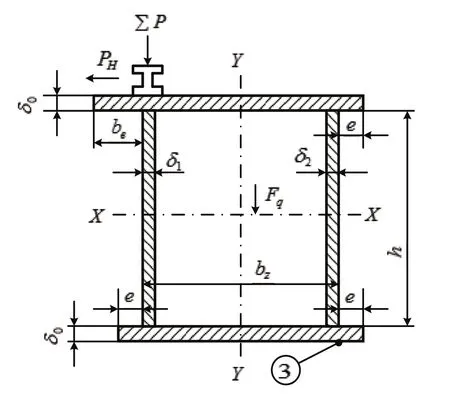
图2 主梁截面图

表2 基本随机变量分布参数表

分别用直接蒙特卡罗法和子集模拟法计算本例的失效概率，结果如表3所示。

表3 工程算例计算结果

该工程算例结果分析显示，在2.2的工程算例中,以静刚度的失效概率为例，当每层的抽样次数N=1000时，子集模拟法的抽样次数为直接蒙特卡罗法的0.05%，而计算误差为22.2%，此时的计算误差还是比较大的；当N=2000，N=3000时，子集模拟法的抽样次数分别为直接蒙特卡罗法的0.1%和0.15%，而计算误差却逐步降低为8.9%和3.7%；由此可见，随着子集模拟法抽样次数的增加，子集模拟法的计算结果越来越接近直接蒙特卡罗法的计算结果，然而子集模拟法的抽样次数仍远远低于直接蒙特卡罗法的抽样次数，由此可见，子集模拟法在计算小失效概率时的计算效率远远高于直接蒙特卡罗法；点3的计算结果具有类似的规律。数值算例和工程算例的结果表明，与直接蒙特卡罗法相比，子集模拟法几乎具有同样的计算精度，且抽样次数大为减少，从而提高了计算效率。

3 结论

1）本文主要介绍了基于M-H抽样方法的子集模拟法，并将子集模拟法应用于桥式起重机主梁的失效概率计算，通过与直接蒙特卡罗法进行对比，验证了所提方法在计算高维小失效概率时的可行性与计算精确度。

2）通过工程算例对比可知，当每层的抽样次数N=1000时，在失效概率降低1个数量级的情况下，蒙特卡罗法的抽样次数扩大为原来的10倍，而子集模拟法仅需增加1个分层的样本数即N=1000即可，此时抽样次数仅为原来的1.2倍，抽样次数的减少是显而易见的。在失效概率为10-6量级，每层的抽样次数N=3000时，子集模拟法的抽样次数仅为蒙特卡罗法的0.018%，效率提高了99.98%。根据大数定律，直接蒙特卡罗法和子集模拟法的计算精度都会随着抽样点数的增加而提高，两种方法的区别是后者与前者相比具有更快的收敛速度，换言之就是：在精度近似一样的情况下，子集模拟法所需抽样点数远小于直接蒙特卡罗法。

在本文的研究背景下，随机变量均为正态分布，若随机变量为非正态分布，可以采用等概率变换原则将非正态变量等效为正态变量即可求解。

[1] 国家标准 GB/T3811-2008.起重机设计规范[M].北京:中国标准出版社,2008.

[2] 邬钱涌,程文明,崔宝祥.岸边集装箱起重机结构轻量化设计及可靠性分析[J].机械设计,2012,29(6):40-43,47.

[3] 叶黔元,陈锦辉,朱胜波.堆垛起重机钢结构体系可靠性分析的蒙特卡罗模拟[J].上海理工大学学报,2006,28(1):83-86,90.

[4] Au S K, Beck J L.A New Adaptive Important Sampling Scheme for Reliability Calculations[J].Structural Safety,1999,21(2):139-163.

[5] Au S K. Probabilistic Failure Analysis by Importance Sampling Markov Chain Simulation[J].Journal of Engineering Mechanics, 2004,130(3):303-311.

[6] Au S K,Beck J L.Estimation of small failure probabilities in high dimensions by simulation[J].Probabilistic Engineering Mechanics, 2001,16(4):263-277.

[7] 曹子君.子集模拟在边坡可靠性分析中的应用[D].成都:西南交通大学,2009.

[8] 张曼,唐小松,李典庆.含相关非正态变量边坡可靠度分析的子集模拟方法[J].武汉:武汉大学学报（工学版）,2012,45(1):41-45,53.

[9] 徐瑞,张家兴,苏成.非平稳随机激励下结构动力可靠度时域显式子集模拟法[J].工程力学,2013,30(7):28-33,39.

[10] 刘佩,姚谦峰.基于子集模拟法的非线性结构动力可靠度计算[J].工程力学,2010,27(12):72-76.

[11] Au S K, Beck J L.Subset simulation and its application to seismic risk based on dynamic analysis. Journal of engineering mechanics. 2003,129(8):901-917.

[12] Au S K,Ching J,Beck J L.Application of subset simulation methods to reliability benchmark problems[J].Structural Safety, 2007,29(3):183-193.

[13] Rubinstein RY.Simulation and the Monte-Carlo method.New York: Wiley,1981.

[14] Fishman GS.Monte Carlo:concepts, algorithm,and applications. New York:Springer,1996.

[15] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,1998:450-454.

[16] Haario H, Saksman E, Tamminen J.Componentwise adaptation for high dimensional MCMC. Computational Statistics,2005,20(2):265-273.

[17] Rosenblatt M.Remarks on a multivariate transformation. Annals of Mathematical Statistics 1952,23:470-472.

[18] 徐格宁.金属装备结构设计（第二版）[M].机械工业出版社，2009.09.