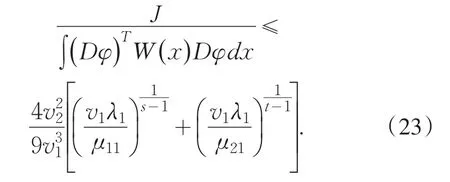2s和2t阶联立微分方程组次特征值的估计
2015-12-20黄振明
黄振明
(苏州市职业大学 基础部,江苏 苏州 215104)
HUANG Zhenming
(Department of Basic Courses,Suzhou Vocational University,Suzhou 215104,China)
2s和2t阶联立微分方程组次特征值的估计
黄振明
(苏州市职业大学 基础部,江苏 苏州 215104)
考虑2s和2t阶阶联立微分方程组在Dirichlet和Neumann边界条件下广义特征值的含权估计,此问题由钱椿林教授提出,是某类六阶微分系统特征值问题的自然延伸,所用方法是Hile和Yeh方法的改进和推广,可用于估计重调和算子等的特征值,笔者引入向量和矩阵符号,运用Sturm-Liouville关于特征值和特征函数空间的定性理论,利用矩阵运算、分部积分、试验函数和Schwartz不等式等具体方法,获到了用主特征值来估计次特征值的显式上界不等式,且其估计系数与所论区间的度量无关,其结论是文献定理的进一步推广.
联立微分方程组;次特征值;权函数;瑞利商;估计
HUANG Zhenming
(Department of Basic Courses,Suzhou Vocational University,Suzhou 215104,China)
CLC mumber:O 157.1 Document code:A Article ID:1674-4942(2015)03-0250-05
1 Introduction
Let(a,b)⊂Rbe an bounded interval.We consider the weighted estimate of second eigenvalue of following 2s and 2t order simultaneous differential system under the Neumann boundary condition as well as Dirichlet
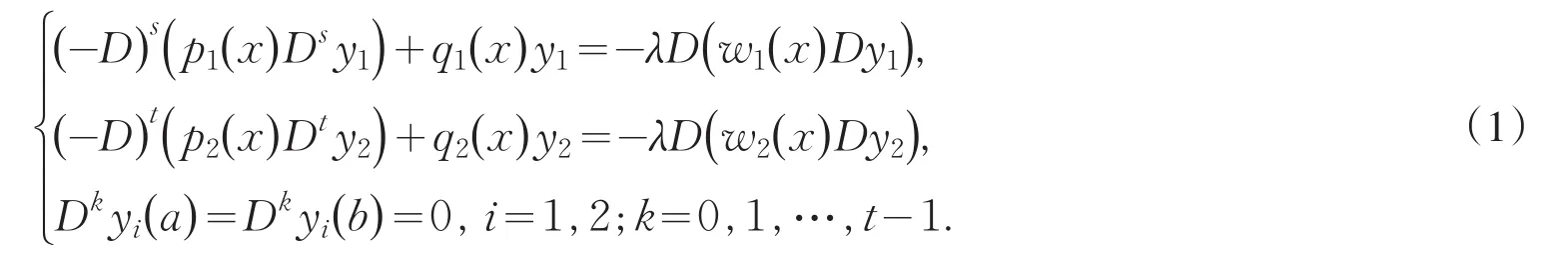
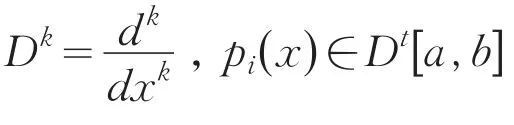
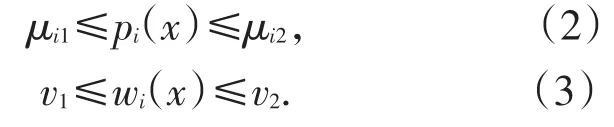
It is important to consider eigenvalue problem of linear differential system,because they involve differ⁃ent fields of science:differential equations,nuclear physics,mechanics and so on.Moreover,they are better models in both pure and applied mathematics.Recently it developed to discuss the generalized eigenvalue prob⁃lem for a single differential equation or a system of equations.A lot of results were gained[1-9].However,it becomes more difficult to estimate their eigenvalue un⁃der some situations such as the case(1),because of the arbitrary even higher order 2s,2t in the system.Us⁃ing methods similar to those of Protter and Hile[10-11],we obtain a broader result than that of Prof.Qian by a somewhat more lengthy arguments.The main achieve⁃ment of the present paper is the establishment of the in⁃equality in the case of 2 For reasoning convenience,throughout the paper we use the following notations: where l,m≥0 are any integers,f is any linear opera⁃tor.So the problem(1)can be changed equivalently in⁃to the following matrix forms: First we explain that the eigenvalues of the system(4)are positive real numbers.We multiply(4)by,in⁃tegrate by parts,use the system and the boundary condi⁃tions in(4).This gives From(5)we know that λ≥0.Furthermore we can claim that λ≠0,or else,then from(5)we know that Dsy1=Dty2=0.We get y1=y2=0 immediately using bound⁃ary conditions.This means that u≡0 which contradicts with the definition of eigenfunction.Thus λ>0.Suppose that the principal and the second eigenvalue of problem(4)are λ1and λ2(0<λ1≤λ2),and the corresponding eigenvector of λ1is u which is normalized in the sense of For briefness,throughout the paper we use the notion∫for.Using integration by parts,from(6)we get By(3)and(7),we have Select the trial vector function φ(x)=(x+c)u,where the coefficient,using integration by parts,the definition of c and(6),we have So φ is weighted orthogonal to u in the generalized sense.Moreover φ satisfy homogeneous boundary condi⁃tions:φ(k)(a)=φ(k)(b)=0(k=0,1,…,t-1),Hence,ac⁃cording to the well-known Rayleigh theorem:the small⁃est Rayleigh-Quotient of any continuous function φ which is orthogonal to the first eigenvector u and satis⁃fies the boundary conditions is the second eigenvalue λ2,we thus obtain Using the definition of φ and(4),we have From(10)we further have Using integration by parts and the equality(x+c)Du= Dφ-u,we find Let us define Combining(11)with(12),yields By(9)and(13),one can find Lemma 1 Suppose that u is the eigenvector of system(4)corresponding to principal eigenvalue λ. Then Proof Since y1and y2are the eigenfunctions of the following eigenvalue problems corresponding to the principal eigenvalue λ1respective⁃ly,then we have according to lemma 1 in[7]: Using integration by parts,(8),Schwarz inequality and(3),we get finishing the proof. Lemma 2 Suppose that u is the eigenvector of system(4)corresponding to principal eigenvalue λ1. Then (1) Proof Using integration by parts,Schwarz in⁃equality,(2),(5),(7)and lemma 1 in[7],we have So lemma 2(1)holds. With the similar process,we can obtain finishing the proof of lemma 2(2). Lemma 3 For J defined as above,the following estimate holds Proof Using the definition of φ and integration by parts,we have After similar calculation,it turns out Finally,using(18),lemma 1 and lemma 2,we finished proof. Lemma 4 Let φ and λ1be as above.Then Proof Using integration by parts and the defini⁃tion of φ,we have By(8)and(19),one can find By Schwarz inequality,(20)and Lemma 1,one obtains So we are done after simplified. Theorem 1 Let λ1,λ2denote the principal and the second eigenvalue of problem(4),then proof of the Theorem 1 We rewrite(14)as where the right-hand side is to be interpreted as infini⁃ty if φ vanishes identically.The lemma 4 can be read as Substituting Lemma 3 and(23)into(22),we obtain the inequality(21)in the theorem 1 immediately after simplified. Remark:Although we’ve gained the estimate of second eigenvalue λ2by λ1of problem(1),however it is unknown whether the inequality(21)still holds or not under other boundary conditions,which needs fur⁃ ther study. [1]Zeng W G,Qian C L.Eigenvalue estimation of Sturm-Li⁃ouville problem[J].Journal of Mathematics for Technology, 1992,8(1):28-32. [2]Liu X T,Chen Z C.The Upper Bound of Eigenvalues for Elliptic Operators of Higher Orders[J].Journal of Universi⁃ty of Science and Technology of China,2002,32(1):37-44. [3]Huang Z M.Estimate of Eigenvalues’Upper Bound for High-Order Differential System[J].Journal of Dongguan University of Technology,2013,20(1):1-6. [4]Jin G Y,Qian C L.Estimates of Eigenvalues for Ordinary Differential Equation with Fourth-Order[J].Journal of Su⁃zhou Institute of Silk Textile Technology,1996,16(4):115-119. [5]Han Q M,Qian C L.The Upper Bound of Second Eigen⁃value of a Class of Differential Equation with Six Orders[J]. Journal of Suzhou University:Nature Science,1999,15(4):26-30. [6]Lu Y P,Qian C L.The Upper Bound Estimate of Second Eigenvalue with General Weight for Differential Equation [J].Journal of Changchun University:Nature Science,2009, 19(10):7-10. [7]Huang Z M,Chen J.Lower Bound Estimate of Ratio of Principal Eigenvalue to Secondary Eigenvalue for Even-Or⁃der Differential Equation[J].Journal of Tonghua Normal University,2014,35(3):24-27. [8]Gao J.On the Upper Bound of Second Eigenvalues for Dif⁃ferential Equation with High Order[J].Journal of Mathe⁃matical Study,1999,32(3):232-237. [9]Zhang C Q,Qian C L.Estimate for the Upper Bound of Second Eigenvalue of a Certain Differential Systems[J]. Journal of Jiansu Radio and Television University,2002,13(6): 34-36. [10]Hile G N,Yeh R Z.Inequalities for Eigenvalues of the Bi⁃harmonic Operator[J].Pacific J Math,1984,112(1):115-132. [11]Hook S M.Domain independent upper bounds for eigen⁃values of elliptic operator[J].Trans Amer Math Soc,1990, 318:615-642. [12]Mark S A.The Universal eigenvalue bounds of Payne-Polya-Weinberger,Hile-Protter,and H C Yang[J].Proc In⁃dian Acad Sci Math Sci,2002,112(1):3-30. [13]Protter M H.Can one hear the shape of a drum?[J].SIAM Rev,1987,29(2):185-197. 责任编辑:毕和平 Estimate of Second Eigenvalue for 2s and 2t Order Simultaneous Differential System In this paper,weighted estimate of generalized eigenvalue for 2s and 2t order simultaneous dif⁃ferential system under the Neumann boundary condition as well as Dirichlet is considered.This problem is the nature extension of the eigenvalue problem of differential system with sixth order,proposed indirectly by prof.Qian.The method used here is the extension with some improvements of Hile and Yeh’s who suc⁃cessively estimate the eigenvalues of biharmonic operator in bibliography.With the symbol of vector and matrix,the inequality of the explicit upper bound of the second eigenvalue is estimated from the principal eigenvalue by using Sturm-Liouville’s qualitative theory of eigenfunction space,matrix operation,integra⁃tion by parts,trial function and Schwartz inequality etc.The estimate coefficients do not depend on the measure of the domain in which the problem is discussed.The results expanded the theorems in the bibli⁃ography. simultaneous differential system;second eigenvalue;weighted function;Rayleigh quotient;es⁃timate 2015-01-08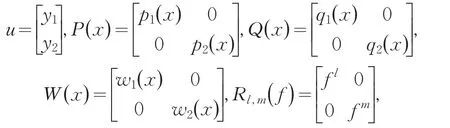
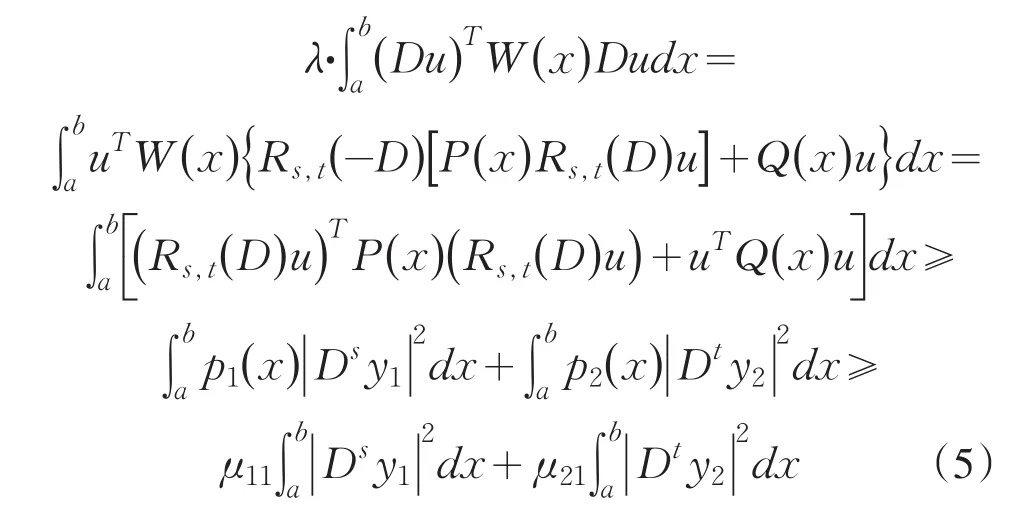

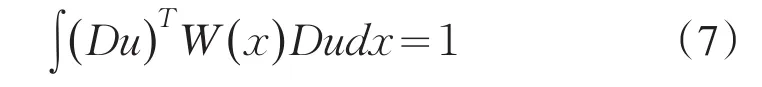







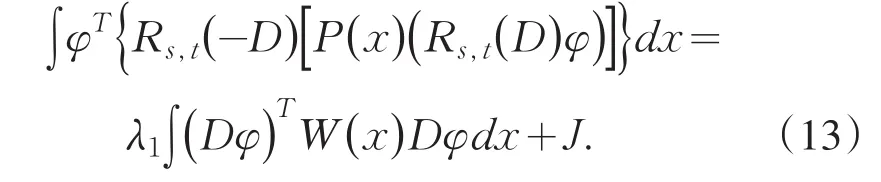
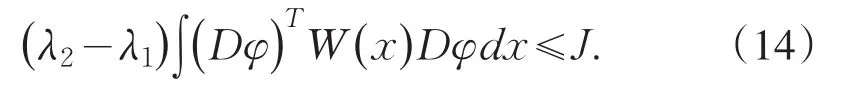

2 Lemmas



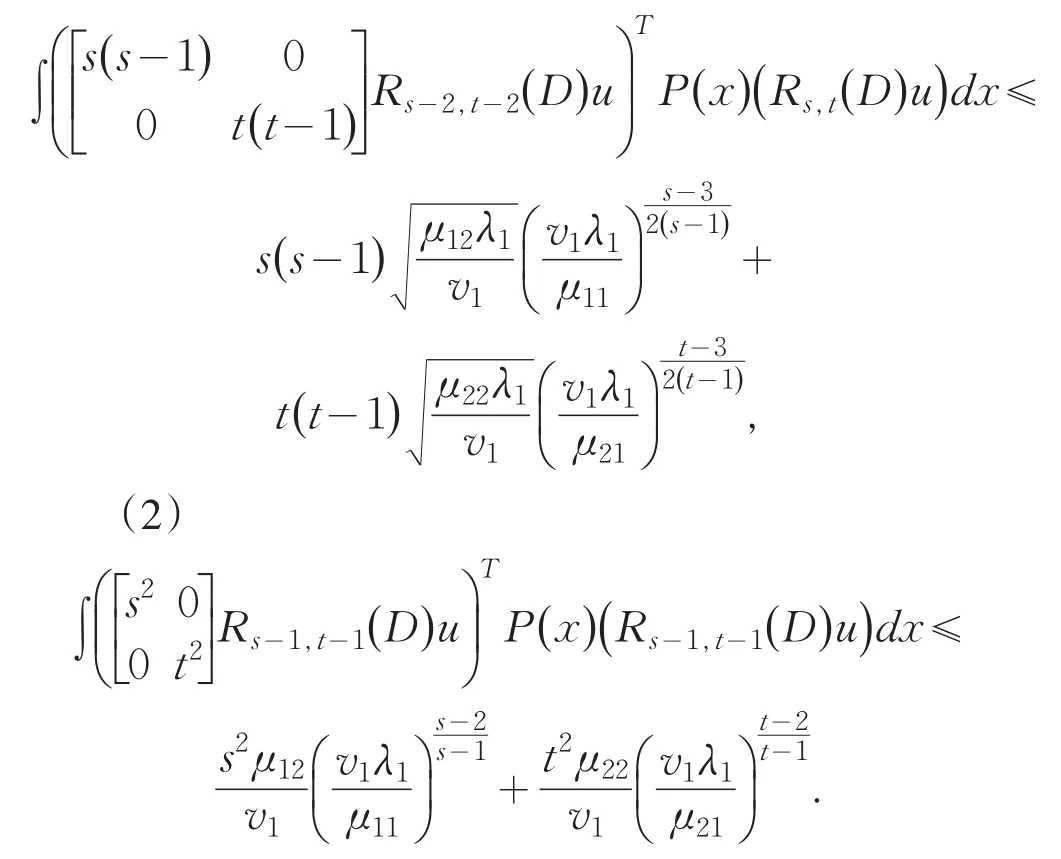
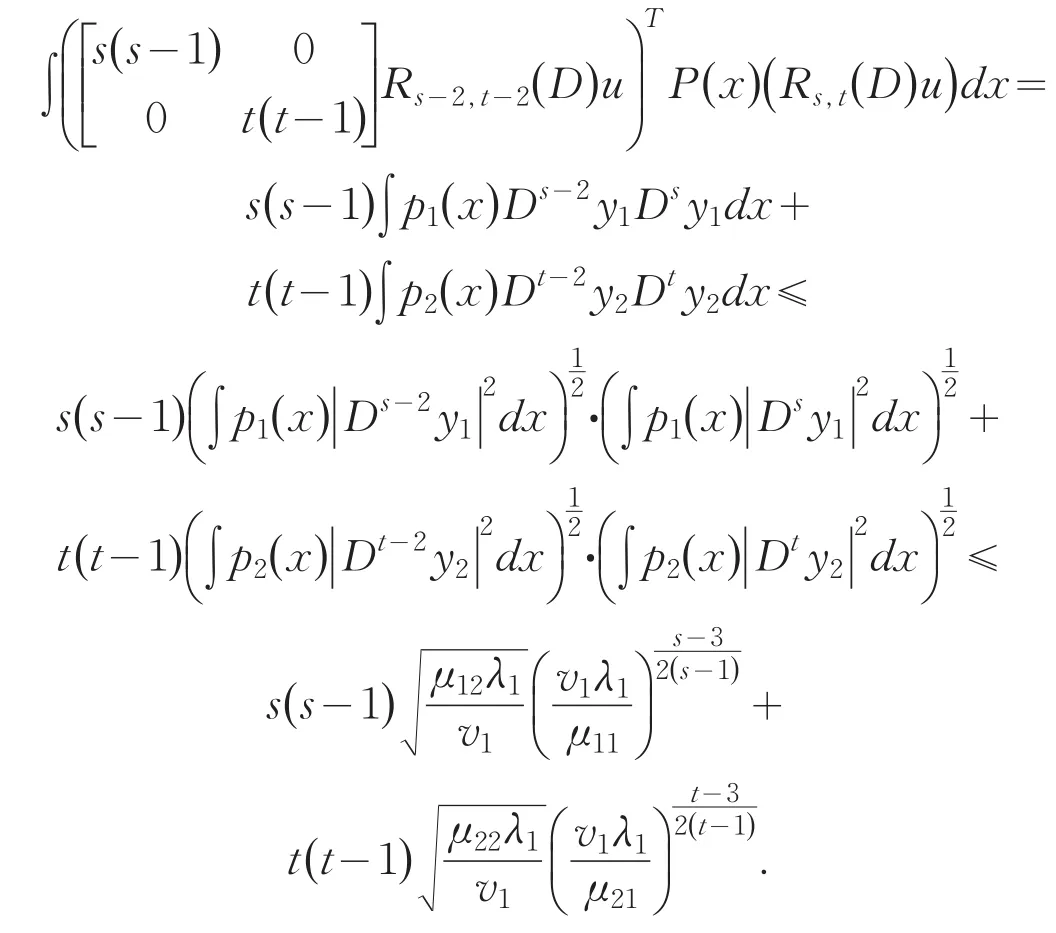
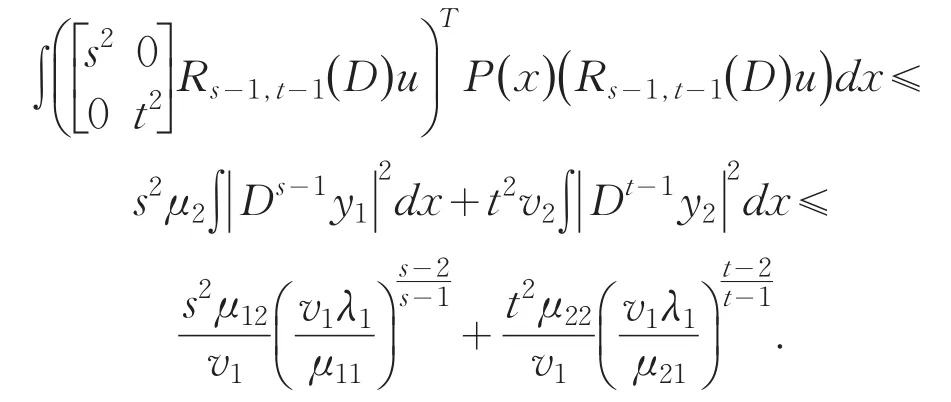







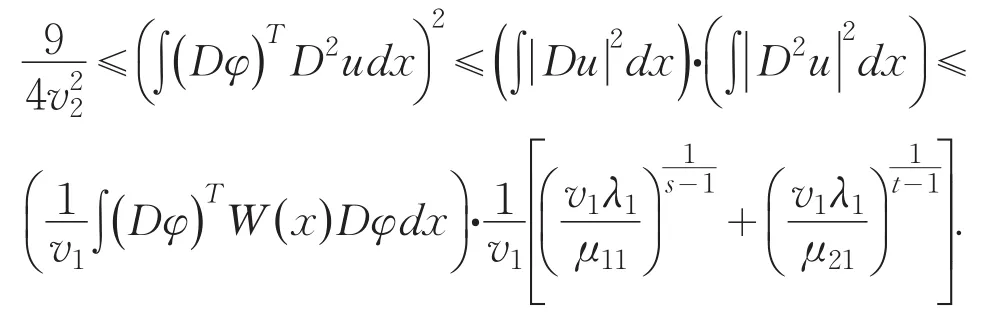
3 Result