李文略

（岭南师范学院 基础教育学院，广东 湛江 524037）

电各向异性介质中无限长矩形腔内电势分布

李文略

（岭南师范学院 基础教育学院，广东 湛江 524037）

电各向异性介质中无限长矩形腔内的电势分布，是拉普拉斯方程的边值问题.腔四壁处均满足第一类非齐次边界条件，不能直接应用分离变量法求解该边值问题.这时，可根据二阶线性齐次偏微分方程解的叠加原理，将该边值问题分解为4个能直接应用分离变量法求解的边值问题来进行求解.求解的方法可作为现有应用分离变量法求解电各向异性介质中拉普拉斯方程边值问题的补充.在令ε11=ε22=ε33=ε的情况下，所得的结果可适用于电各向同性介质.

电各向异性介质；边值问题；分离变量法；叠加原理；半幅傅里叶级数；矩形腔

陈燊年等系统地研究了介质为各向异性的电磁场[1-2]，其中有将分离变量法引进研究电各向异性介质中拉普拉斯方程的边值问题，并举两例作应用示范，所举之例的边界条件是不全为第一类齐次边界条件的，可满足直接应用分离变量法求解.分别以“分离变量法”和“电各向异性介质”为检索词在中国知网上进行模糊搜索，只发现1篇研究电各向异性介质分离变量法的文献[3]，其所举求解电各向异性介质中线电荷与两接地导体平面间的电势分布和电解槽的电势分布的例子，其边界条件均满足直接应用分离变量法求解的条件.鉴于有关研究电各向异性介质分离变量法的文献较为稀少，本文将在前人研究[1-2]的基础上，以求无限长矩形腔内的电势分布为例（不满足直接应用分离变量法求解的条件），间接应用分离变量法求电各向异性介质中拉普拉斯方程的边值问题，而其边界条件均是第一类非齐次边界条件.

1 无限长矩形腔内的电势分布

无限长矩形腔沿着电各向异性介质的主轴坐标系O-x1x2x3的x3轴放置（见图1），其四壁的电势分布为φ1、φ2、φ3、φ4，求腔内的电势分布.

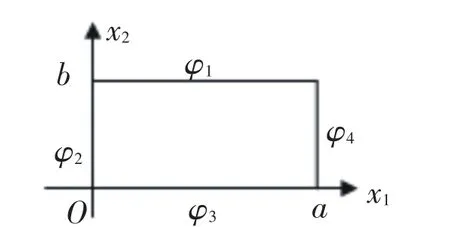
图1 矩形腔截面图Fig.1 Section of rectangular

矩形腔无限长且内部无电荷，故腔内的电势与x3无关，满足电各向异性介质的二维拉普拉斯方程[1].求腔内的电势分布即是求解边值问题

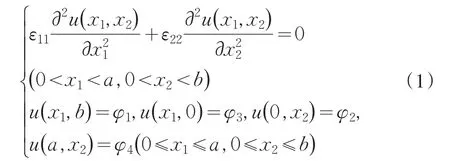
式中：ε11、ε22分别为沿着x1轴和x2轴正方向的介电常数.

边值问题式（2）的第一类边界条件均是非齐次的，无法直接应用分离变量法求解.现将边值问题式（2）分解为四个边值问题：

边值问题1-4均可应用分离变量法直接求解.现求解边值问题1，设泛定方程存在分离变量的形式解，代入式（3）中的泛定方程

由式（9）求得C=D=0，故u1(ξ1,ξ2)=0为平庸解.

若λ>0，结合边界条件式（9），式（7）的本征值和本征函数为

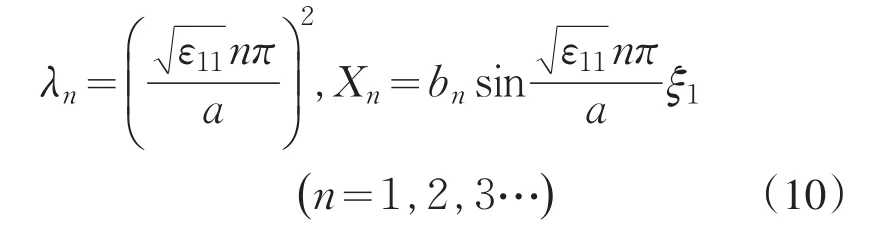
其中bn为任意常数.将λn代入式（8）中解出Y()ξ2的通解

其中An=bndn.因式（3）中的泛定方程是线性齐次的，根据叠加原理将本征解叠加在一起，构成一般解

式（14）就是边值问题1的一般解，其中系数An由是（16）确定.

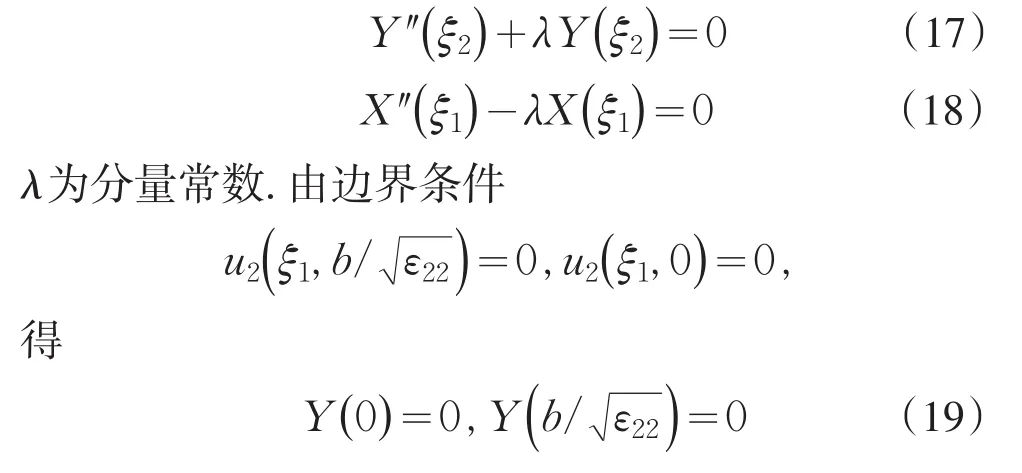
若λ=0或λ<0，结合式（19），解式（17），均得，为无意义的平庸解.

若λ>0，结合式（19），式（17）的本征值和本征函数为

其中Bn=bnBξn.因式（4）中的泛定方程是线性齐次的，根据叠加原理将本征解叠加在一起，构成一般解

现确定式（25）中的系数Bn.将u2（0，ξ2）=φ2代入上式，得

式（25）就是边值问题2的一般解，其中系数Bn由是（27）确定.

式（28）就是边值问题4的一般解，其中系数Dn由是（29）确定.

式（30）就是边值问题3的一般解，其中系数Cn由是（31）确定.

由于边值问题式（2）中的泛定方程的线性性质，它的解是边值问题1-4解的线性和，即

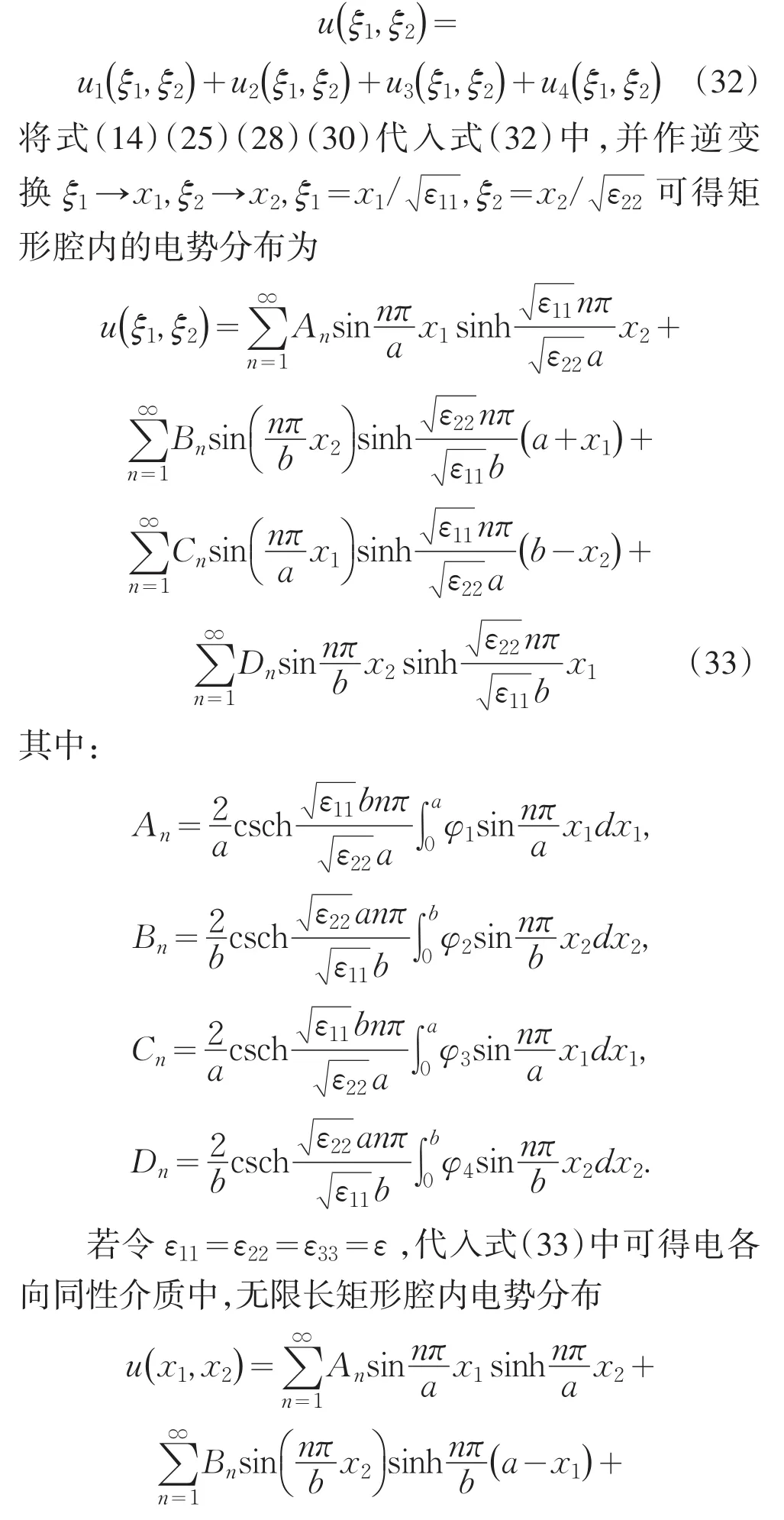
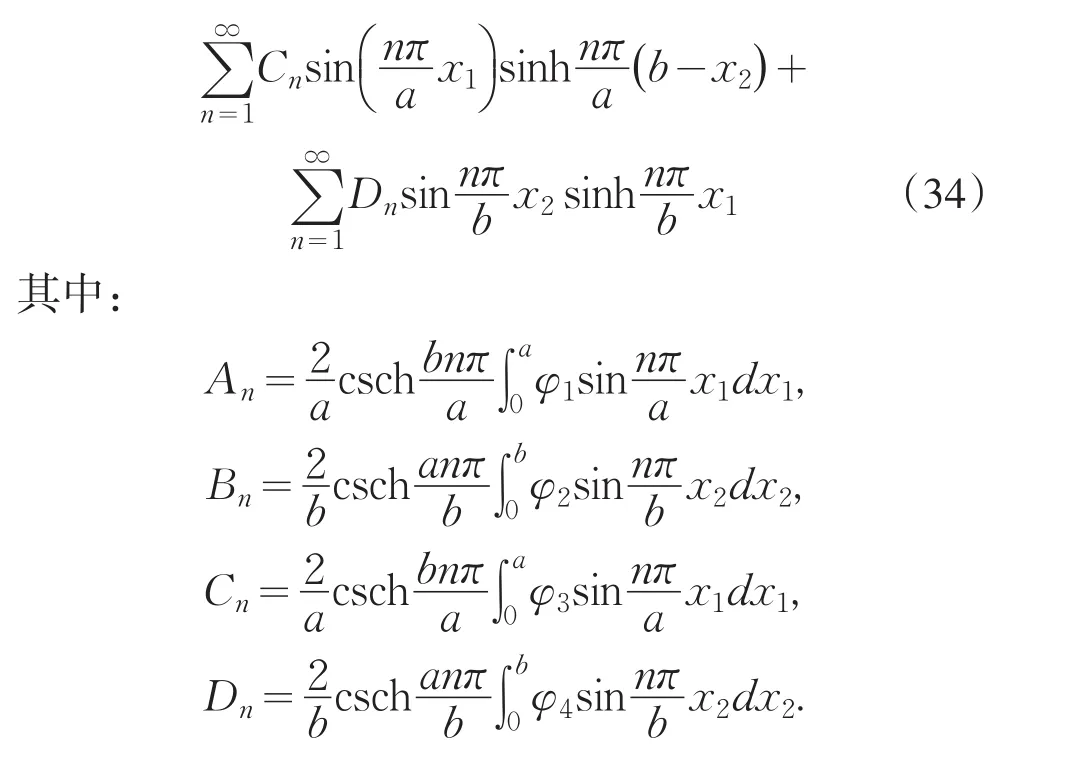
2 结语

分离变量法是求电各向异性介质的拉普拉斯方程边值问题的解析方法.求解电各向异性介质中诸如式（1）的拉普拉斯边值问题时，需先作坐标变换得到边值问题式（2）.但式（2）的第一类边界条件均是非齐次的，不满足直接使用分离变量法求解的条件.这时，可根据二阶线性齐次偏微分方程解的叠加原理，将该边值问题分解为4个能直接应用分离变量法求解的边值问题进行求解，即将求边值问题1-4的结果线性叠加即可得到边值问题式（2）的解.求解文中所述的拉普拉斯方程边值问题的方法可作为现有应用分离变量法求解电各向异性介质中拉普拉斯方程边值问题的补充.

[1]陈燊年,洪清泉,王建成.介质为各向异性的电磁场[M].北京:科学出版社,2012:88-104.

[2]林文枝,陈燊年.椭圆环电流在各向异性介质中的磁场[J].华侨大学学报:自然科学版,1993,17（3）:87-92.

[3]苏武浔,陈芳,陈燊年.各向异性介质静电势微分方程的分离变量法[J].华侨大学学报:自然科学版,1997,18（1）: 87-92.

[4]顾樵.数学物理方法[M].北京:科学出版社,2014:26.

责任编辑：刘 红

Potential Distribution in An Infinite Rectangular Cavity in Anisotropic Dielectric

LI Wenlüe
（College of Basic Education，Lingnan Normal University，Zhanjiang 524037，China）

Potential distribution in an infinite rectangular cavity in anisotropic dielectric is a boundary value problem of La⁃place equation.Because the walls of the cavity meet the first nonhomogeneous boundary conditions,the Laplace equation boundary value problem cannot be solve directly by applying variable separation methods.According to the superposition principle of the solutions of the two order linear homogeneous partial differential equations,the boundary value problems which are divided into 4 boundary value problems can be solved directly by using method of separation of variables.The method can be used as a supplementary method for solving the boundary value problem of Laplace equation by applying method of separation of variables in anisotropic dielectric.The results can be applied to isotropic dielectric in the situation：ε11=ε22=ε33=ε.

anisotropic dielectric；value problem；method of separation of variables；superposition principle；half-range Fourier series；rectangular cavity

O 441.4

A

1674-4942（2015）03-0257-04

2015-07-08