范水平，陈宗煊

(华南师范大学数学科学学院，广州510631)

1 引言和主要结果

本文假设读者熟悉亚纯函数的值分布理论和标准记号［1－2］，σ(f)和σ2(f)分别表示亚纯函数的增长级和超级. 为了更精确地估计微分方程解的增长性，首先回顾以下定义.

定义1［3］假设f(z)是复平面上的亚纯函数，

则f(z)的超级σ2(f)定义为

定义2［4］给定一个集合E，它的线测度和对数测度分别定义为

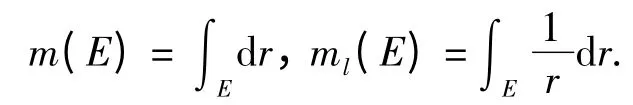
本文考虑微分方程

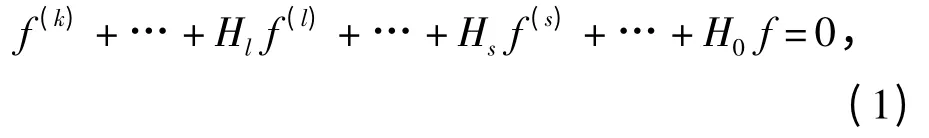
其中Hj(z)为整函数. 当k=2 时，方程为

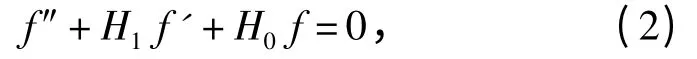
其中H1(z)或H0(z)是超越整函数. 如果f1和f2是方程(2)的2个线性无关的解，则f1和f2中至少有1个具有无穷级［5］. 另一方面，对于方程(2)，存在具有有穷级解的情况. 例如:f=e－z满足方程

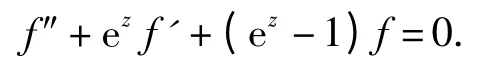
对于方程(2)，一个很自然的问题:Hj(z)(j =0，1)需要满足什么条件才能保证方程(2)的每个解f 具有无穷级?关于这方面的工作已经有很多，Gundersen［6］、Hellerstein 等［7－8］研究了此类方程的非平凡解具有无穷级的条件，列举如下:

(i)σ(H1(z))＜σ(H0(z))＜1/2;

(ii)H1(z)是多项式，H0(z)是超越整函数.

更多的结果可参考文献［7］、［9］、［10］，对进一步研究整函数系数微分方程解的无穷级的精确估计具有一定的价值.

对于高阶齐次线性微分方程(1)，当方程系数满足什么条件可以保证方程的每个非零解具有无穷级?如何更加精确地估计无穷级解的增长性?2003年，Chen［11］进行了研究，并得到:

定理1［11］假设aj(j =0，1，…，k－1)是复数，存在as和al，使得l ＞s，as=dseiφ，al=－dleiφ，ds＞0，dl＞0，对j≠s，l，aj=djeiφ(dj≥0)或aj=－djeiφ，max{dj;j≠s，l}=d ＜min{ds，dl}，如果Hj=hjeajz，hj是多项式，且hshl≢0，则微分方程(1)的每个超越解f 满足σ(f)=∞且σ2(f)=1.

2005年，江良英和陈宗煊［12］继续研究方程(1)的解的增长性，并得到:

定理2［12］假设Hj(z)=hj(z)ePj(z)(j =0，1，…，k－1)，Pj(z)是首项系数为aj的n (n≥1)次多项式，hj(z)为整函数，σ(hj(z))＜n，aj是复数，存在as和al，使得l ＞s，as=dseiφ，al=－dleiφ，ds＞0，dl＞0. 对j≠s，l，aj=djeiφ(dj≥0)或aj=－djeiφ，max{dj;j≠s，l}=d ＜min{ds，dl}，hshl≢0，则微分方程(1)的每个超越解f 满足σ(f)=∞.

本文继续研究方程(1)，得到了方程(1)的非零解的超级的精确估计，得到如下结果.

定理3 假设Hj(z)=hj(z)ePj(z)(j =0，1，…，k－1)，Pj(z)=ajzn，hj(z)为整函数且σ(hj(z))＜n，aj是复数，存在as和al，使得l ＞s，as=dseiφ，al=－dleiφ，ds＞0，dl＞0，对j≠s，l，aj=djeiφ(dj≥0)或aj=－djeiφ，max{dj;j≠s，l}=d ＜min{ds，dl}，hshl≢0，则微分方程(1)的每个超越解f 的超级满足σ2(f)=n.

定理4 假设Hj(z)=hj(z)ePj(z)(j =0，1，…，k－1)，Pj(z)=ajzn，hj(z)为整函数且σ(hj(z))＜n，aj是复数，存在as和al，使得l ＞s，as=dseiφ，al=－dleiφ，ds＞0，dl＞0，对j≠s，l，aj=djeiφ(dj≥0)或aj=－ djeiφ，max{dj;j≠s，l}= d ＜min{ds，dl}，hshl≢0，gj(j =0，1，…，k－1)是多项式，则微分方程

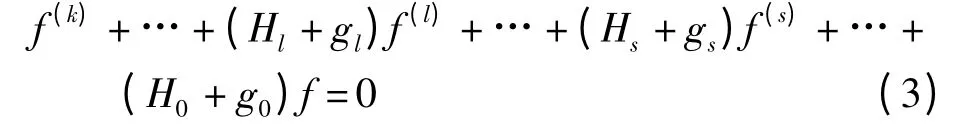
的每个超越解f 满足σ(f)=∞及σ2(f)=n.

2 证明所需要的引理

引理1［11］假设Aj(j =0，1，…，k－1)是有穷级整函数，若f 是方程

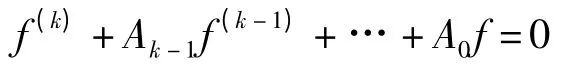
引理2［11］假设f(z)是一个具有无穷级的整函数且σ2(f)=α ＜+∞，E⊂［1，∞)具有有穷对数测度，则存在一个无穷点列{zk= rkeiθk}(k =1，2，…)，使得|f(zk)| =M(rk，f)，θk［0，2π)}，=θ0［0，2π)，rkE，rk→∞和对任意的ε ＞0 和充分大的rk，有

其中v(rk)是f(z)的中心指标.

引理3［11］假设f(z)是超越整函数，则存在对数测度为有限的集合E⊂{(1，∞)}，使得当我们取z满足|z| =r(［0，1］∪E)，|f(z)| =M(r，f)时，有

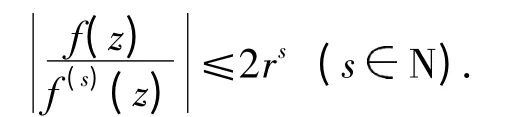
引理4［13］假设f(z)是超越亚纯函数，Γ ={(i1，j1)，…，(im，jm)}是一个由整数对所构成的有限集合且满足jn＞in≥0 (n =1，…，m)，α ＞1，ε＞0 是给定的常数. 则下列结论成立:

(i)存在一个具有线测度为零的集合E1⊂［0，2π)，且存在仅依赖于α 与Γ 的常数B ＞0，使得对于ψ0(［0，2π)－E1)，存在一个常数R0=R0(ψ0)＞0，对所有满足|z|≥R0，arg z=ψ0的z 和(i，j)Γ，有

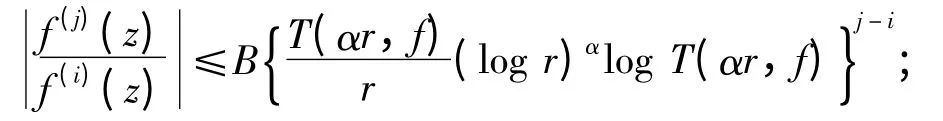
(ii)存在一个具有有穷对数测度的集合E2⊂［1，∞)，且存在仅依赖于α 与Γ 的常数B ＞0，使得对所有满足|z|(E2∪［0，1］)的z 和(i，j)Γ，(i)的结论成立;

(iii)存在一个具有有穷线测度的集合E3⊂［1，∞)，且存在仅依赖于α 与Γ 的常数B ＞0，则对所有满足|z|(E3∪［0，1］)的z 和(i，j)Γ，有

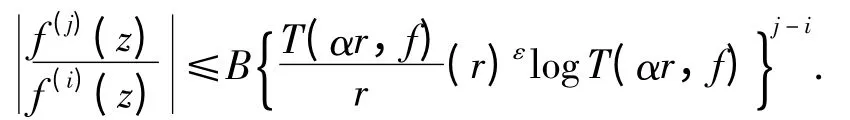
引理5［14］假设P(z)=deiφzn+…(d ＞0)是一个n (n≥1)次多项式，A(z)(≢0)是整函数且σ(A)＜n，假设g(z)=A(z)eP(z)，z =reiθ，那么对任意给定的ε ＞0，存在线测度为零的集合H1⊂［0，2π)，满足对任意θ(［0，2π)－(H1∪H2))，存在R ＞0，对所有满足|z| =r ＞R 的z，下列情形之一成立:

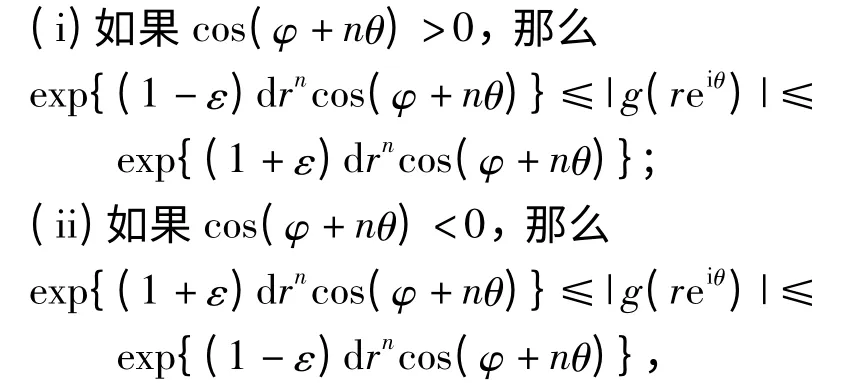
其中H2={θ［0，2π);cos(φ+nθ)=0}是有限集.

引理6［15］假设g:(0，∞)→R，h:(0，∞)→R，二者都是单调递增函数，除去一个对数测度有限的例外集E 外满足g(r)≤h(r)，则对于任意α ＞1，存在r0＞0，使得对所有r ＞r0，g(r)≤h(αr)成立.

3 定理的证明

定理3 的证明 假设f(z)是方程(1)的超越解，由引理1 可知，σ2(f)≤n，只需要证明σ2(f)≥n.

由定理2 可知，σ(f)=∞. 若方程(1)的系数如定理3 所假设，我们断言:方程(1)的非零解f 的超级均满足σ2(f)=n.

我们采用反证法. 假设σ2(f)=α ＜n，下面证明假设不成立，从而完成定理的证明.

由引理4，存在一个具有有限对数测度的集合E1⊂［1，∞)，且存在仅依赖于α 与Γ 的常数B ＞0，使得对所有满足|z|(E1∪［0，1］)的z 和(i，j)Γ，下列不等式成立(取α=2):

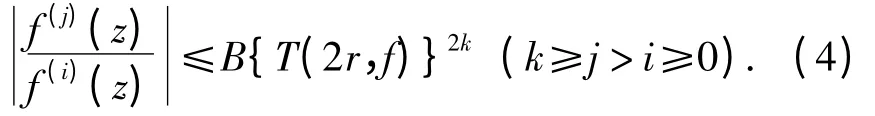
由Wiman-Valiron 理论，有:

由引理2，可以选取一个点列{zm=rmeiθm}(m=1，2，…)，使得|f(zm)| = M(rm，f)，θm［0，2π)}，［0，2π)，rm(［0，1］∪E1∪E2)，rm→∞，对于任给的ε1(0 ＜3ε1＜min{1－α，(ds－d)/ds})和充分大的rm，有

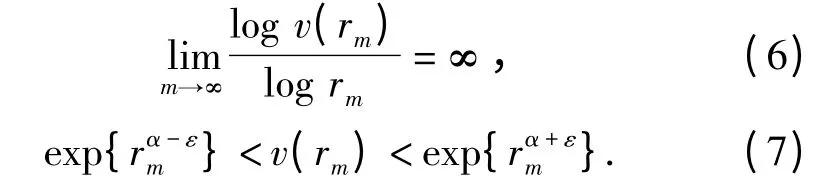
令Ps(z)=aszn，Pl(z)=alzn，as=dseiφ，al=－dleiφ，z = reiθ0. 对于上面的θ0，有Re{aszn}=dsrncos(φ +nθ0)，Re{alzn}=－dlrncos(φ +nθ0).对于cos(φ+nθ0)，有3 种情形:(i)cos(φ+nθ0)＞0;(ii)cos(φ+nθ0)＜0;(iii)cos(φ+nθ0)=0.

下面分别考虑这3 种情形.

情形(i):cos(φ+nθ0)＞0. 由式(1)，有

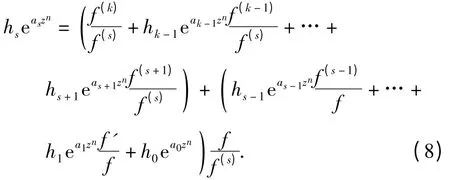
对于充分大的m，θm→θ0，cos(φ+nθm)＞0. 由引理5 可知，对于任意的ε ＞0，存在一个线测度为零的集合H1⊂［0，2π)，满足对任意θ(［0，2π)－(H1∪H2))，其中H2={θ［0，2π);cos(φ+nθ)=0}，存在R1＞0，使得对所有满足|z| =r ＞R1的z及充分大的m，可知θm满足

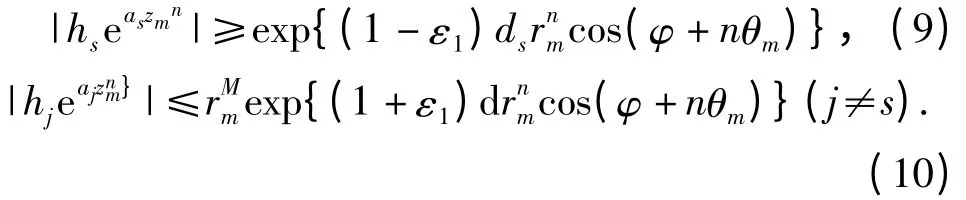
由引理3，存在对数测度为有限的集合E3⊂(1，∞)，使得取zm满足|zm| =rm(［0，1］∪E3)，|f(zm)| =M(rm，f)时，有

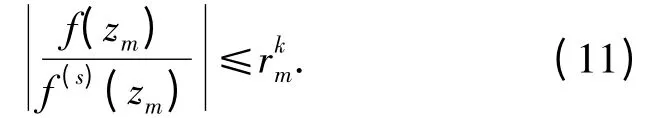
对于点列{zm=rmeiθm}，由式(4)、(8)～(11)，当m 充分大时，可得

故有

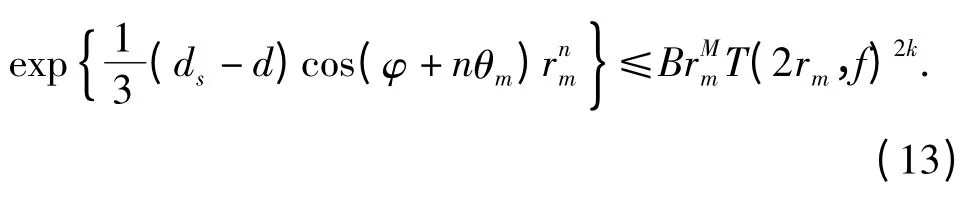
由式(13)及引理6，立即得到σ2(f)≥n.

情形(ii):cos(φ+nθ0)＜0. 用hlealzn代替hseaszn并且用情形(i)中相同的理由，可以得到σ2(f)≥n.

情形(iii):cos(φ+nθ0)=0. 由于zm=rmeiθm满足对于充分大的m，rm→∞，θm→θ0，射线arg w =φ+nθ0是}(j=0，…，k－1)的一条渐近线，故存在N ＞0，当n ＞N 时，由，对j=0，…，k－1，有

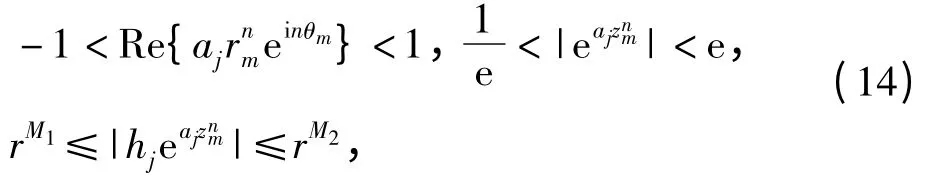
其中M1和M2是2个正常数. 由式(1)、(5)和式(14)，有

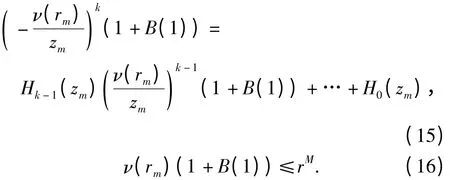
式(16)与式(6)矛盾. 故假设不成立.

结合引理1，σ2(f)=n. 证毕.

定理4 的证明 运用类似定理3 的证明方法，可以证明定理4.

［1］杨乐. 值分布及其新研究［M］. 北京:科学出版社，1982.

［2］Hayman W K. Meromorphic functions［M］. Oxford:Clarendon Press，1964.

［3］仪洪勋，杨重骏. 亚纯函数唯一性理论［M］. 北京:科学出版社，1995.

［4］Hayman W K. On the characteristic of functions meromorphic in the plane and of their integrals［J］. Proceedings of the London Mathematical Society，1965，14A(3):93－128.

［5］Hile E. Ordinary differential equations in the complex domain［M］. New York:Wiley，1976.

［6］Gundersen G. Finite order solutions of second order linear differential equations［J］. Transactions of the American Mathematical Society，1988，305(1):415－429.

［7］Hellerstein S，Miles J，Rossi J. On the growth of solutions of f″+A1(z)f' +A0(z)f =0［J］. Transactions of the American Mathematical Society，1991，324(2):693－706.

［8］Hellerstein S，Miles J，Rossi J. On the growth of solutions of f″+gf' +hf =0［J］. Annales Academiae Scientiarum Fennicae-mathematica，1992，17(2):343－365.

［9］Chen Z X. The growth of solutions of second order linear differential equations with meromorphic coefficients［J］.Kodai Mathematical Journal，1999，22(2):208－221.

［10］Kwon K H，KIM J H. Maximum modules satisfying second order linear differential equations［J］. Kodai Mathematical Journal，2001，24(3):344－351.

［11］Chen Z X. On the hyper order of solutions of higher order differential equations［J］. Chinese Annals of Mathematics:Series B，2003，24(4):501－508.

［12］江良英，陈宗煊. 某类高阶整函数系数微分方程解的增长性［J］. 江西师范大学学报:自然科学版，2005，29(1):12－14.Jiang L Y，Chen Z X. The growth of solutions of higher order differential equations with entire coefficients［J］.Journal of Jiangxi Normal University:Natural Sciences Edition，2005，29(1):12－14.

［13］Gundersen G. Estimates for the logarithmic derivative of a meromorphic function，plus similar estimates［J］. Journal of the London Mathematical Society，1988，37(2):88－104.

［14］高仕安，陈宗煊，陈特为. 线性微分方程的复震荡理论［M］. 武汉:华中理工大学出版社，1995.

［15］Hayman W K. The growth of power series:A survey of the Wiman-Valiron method［J］. Canadian Mathematical Bulletin，1974，17:317－358.