☉内江师范学院数学与信息科学学院 谢志强 罗仕明

试析一道推广的高考试题所蕴含的数学思想

☉内江师范学院数学与信息科学学院 谢志强 罗仕明

一、提出问题

题目（2012年江西高考数学文科第5题）观察下列事实：|x|+|y|=1的不同整数解（x，y）的个数为4，|x|+|y|=2的不同整数解（x，y）的个数为8，|x|+|y|=3的不同整数解（x，y）的个数为12，…，则|x|+|y|=20的不同整数解（x，y）的个数为（）.

A.76B.80C.86D.92

此题是关于数列的应用题.观察可得不同整数解的个数可以构成一个首项为4，公差为4的等差数列，则所求为第20项，得到结果为80.即|x|+|y|=k的不同整数解（x，y）的个数为f（k）=4k.对于此问题，求解较为简单，为了让学生对认知的深化，开拓思维的视野，并能培养发现问题、提出问题、分析问题和解决问题的能力，本文对此问题进行变形推广，得到一个关于绝对值不等式的整数解问题，通过分析发现此类问题蕴含着丰富的数学思想.下面提出问题：求解满足不等式|x|+|y|＜k（k∈N+）的整数解（x，y）的个数？

二、解决问题

1.利用归纳的数学思想解决问题

（1）枚举归纳.

数学归纳推理的目的在于寻找隐藏在特殊事例之中的量性模式，其中量性模式是指按照某种理想化的要求或实际可应用的标准，来反映或概括表现一类或一种事物关系结构的数学形式.［1］为了解决此类不等式，不妨以简单的枚举归纳法求解，依据某种属性在部分同类对象中的不断重复而没有遇到反例，从而推出该类的所有对象都具有这种性质的归纳推理.

为了方便枚举满足不等式|x|+|y|＜k（k∈N+）的整数解（x，y），令f（k）表示整数解的个数.枚举如下：

当k=1时，整数解有（0，0），即f（1）=1.

当k=2时，整数解有（0，0）、（0，±1）、（±1，0），即f（2）=5.

当k=3时，整数解有（0，0）、（0，±1）、（±1，0）、（0，±2）、（±2，0）、（±1，±1），即f（3）=13.

当k=4时，整数解有（0，0）、（0，±1）、（±1，0）、（0，±2）、（±2，0）、（±1，±1）、（0，±3）、（±3，0）、（±1，±2）、（±2，±1），即f（4）=25等.

于是，可以归纳出满足不等式|x|+|y|＜k的整数解（x，y）的个数为：f（k）=1+4×1+4×2+…+4（k－1）=1+2k（k－1）.

（2）要素归纳.

要素归纳模式是指通过探讨所考虑对象的构成要素及其构成方式而发现规律的思维方式，其核心是探寻具有一致性的量性结构.如果在平面直角坐标系上看待此类问题的解，由上面的枚举归纳可得出组成不等式的整数解可以分成三类：原点、坐标轴上的点、象限内的点.

此处以|x|+|y|＜4的整数解（x，y）为例进行分析，满足此不等式的解可看作平面直角坐标系上的点，得到以下结论：原点个数有1个，即（0，0）；坐标轴上的点有12个，即（0，±1）、（±1，0）、（0，±2）、（±2，0）、（0，±3）、（±3，0）；象限内的点有12个，即（±1，±1）、（±1，±2）、（±2，±1）.同理，可得到当k取不同值时，满足不等式的解的不同讨论情况，具体如表1.

表1 满足不等式的整数解的讨论情况表

（3）函数归纳.

函数归纳模式是指：将所考查的特殊事例的数量顺次排列组成一个数列，把这些数量看作是某个关于正整数n的函数f（n）的函数值，然后通过分离常量与自变量n或联想所熟知的函数而找到函数关系式的思维方式.于是，对表1中最后一列数据利用函数归纳模式，得到：f（1）=1=（1－1）2+12，f（2）=5=（2－1）2+22，f（3）=13=（3－1）2+32，f（4）=25=（4－1）2+42，f（5）=41=（5－1）2+52，f（6）=61=（6－1）2+ 62，…，由上面6个式子可以归纳为：f（k）=（k－1）2+k2.

（4）递推归纳.

递推归纳模式是指：在数列中，通过探讨由已知项“生出”未知项的结构方式，从而发现一般规律的一种思维方式，其核心是归纳出相邻两项间的递推关系.［1］在具体运用中，最为有效的策略是考查相邻两项的差的特点，因为“差”在减小数值的同时往往也降低了所考查对象的“维度”.

对于此题，该整数解的个数构成的数列为1、5、13、25、41、61、85、…，则此题转换为求该数列的通项.直接求此数列的通项较为复杂，但是考查相邻两项的差构成的数列为4、8、12、16、…，在重复地用后一项减去它前一项.将此数列写出杨辉三角形式，便可得到以下三角形式.

在上述三角形式中可以看出第二行的数成等差数列，第三行是成常数列.由此可以推测出此问题的解的个数构成的数列为二阶等差数列.若记此数列为｛（fk）｝（其中（f1）=1），易得到（fk）满足递推关系（fk）=（fk－1）+ 4（k－1），其中k≥2.采用叠加的方法便可得到（fk）=2k（k－1）+1.

2.利用化归的数学思想解决问题

所谓“化归”，是指把待解决的问题，通过转化过程，归结到一类已经解决或者比较容易解决的问题中去，最终求得原问题解答的一种手段和方法.

首先，“以退为进”寻找解决方法.不妨这样思考，对于“满足不等式|x|＜k（k∈N+）的整数解”可以退化为“满足x＜k（k∈N+）的非负整数解”.令（fk）表示解的个数，由于x＜k的非负整数解的个数为（fk）=C1k－1+1，则满足不等式|x|＜k的整数解的个数为（fk）=2C1k－1+1.

然后，回归到本题，本题是一个含有两个未知数的绝对值不等式|x|+|y|＜k（k∈N+）.可以先不忙考虑绝对值，将问题退化为x+y＜k（k∈N+），然后再将问题转化为x＜k－y.由于此不等式的非负整数解同上，于是可以得到|x|＜k－y的整数解的个数（fk）=2C2k+1.故|x|+|y|＜k的整数解的个数为（fk）=4C2k+1，与以上四种归纳模式所得的结果具有一致性.

3.利用演绎的数学思想解决问题

上述的所有结论都是通过合情推理而得到，其结果的正确性还没有被验证.故以下运用演绎的方法来证明.下面运用数学归纳法来进行证明所得到的结论：（fn）=1，证明过程如下：

首先，当n=1时，（f1）=1.当n=2时，易验证结论成立.

故满足不等式|x|+|y|＜k（k＞0）的整数解（x，y）的个数为（fk）=

三、推广问题

推广1：求满足不等式|x1|+|x2|+|x3|＜k（k∈N+）的整数解（x1，x2，x3）的个数.

分析：运用类比的思维方式，由于在上述问题中含有两个未知量是在平面直角坐标系中进行要素归纳，故三个未知量则要在空间直角坐标系中进行要素归纳，构成整数解（x1，x2，x3）的要素有：原点，坐标轴上的点，xOy、yOz、xOz平面上的点，象限内的点.易归纳得到满足不等式|x1|+|x2|+|x3|＜k（k∈N+）的整数解（x1，x2，x3）的个数为x2，…，xn）的个数.

分析：利用递推归纳法，|x1|＜k（k∈N+）的整数解的个

以此类推，只需找出其系数的递推关系，得到以下“类杨辉三角形式”.令n为绝对值不等式中未知量的个数，得到：

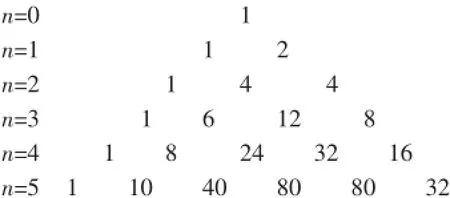
记上述三角形中第n+1行中第r+1个数为Srn，受杨辉三角启发，从三角形中易看有每一个数等于它左肩上与右肩上的数字之此启发，可以得到类似的关r≤n-1），即满足不等

对于推广2和推广3的具体证明这里略去，具体证明可以参阅文2.

四、结束语

对于上述几个推广的解答依次运用了归纳推理、类比推理和演绎推理比较完整地经历了数学发现的全过程.先由归纳推测出结论，然后由类比发现规律，最后由演绎证明结论和规律.按照著名数学家陈省生提出的“好”数学的标准：“只有数学思想方法深刻，能进一步引身、推广、发展的数学才是好的数学.”［3］上述几个推广尤其是推广2就属于“好”数学.此外，数学思想方法具有隐喻性的特点，它隐于知识内部，特别是隐含在好的数学问题之中.应多层面、多角度地对数学问题进行深入挖掘，才能使所隐含的数学思想和方法显性化.才能够充分发挥数学问题在帮助学生学会数学地思考问题.

1.王新民.试析一道课本习题中所蕴含的数学思想［J］.中国数学教育（高中版），2013（9）.

2.徐利治.数学分析的方法及例题选讲——分析学的思想、方法与技巧［M］.大连：大连理工大学出版社，2007.

3.涂荣豹，王光明，宁连华.新编数学教学论［M］.上海：华东师范大学出版社，2006.F