傅俊义,王三华

(南昌大学数学系,江西 南昌 330031)

关于《拓扑向量空间中的一类平衡问题研究》的注记

傅俊义,王三华

(南昌大学数学系,江西 南昌 330031)

利用比较弱的锥连续性与著名的Fan-KKM定理,得到一类具有控制结构的强向量均衡问题的解,并讨论其解集的性质,改进了相关文献的主要研究结果.

强向量均衡问题;锥连续;控制结构;解集

1 引言

均衡问题是变分不等式与相补问题的有意义的推广.在力学、微分方程理论、控制论、优化理论与数理经济等领域的很多问题,都可化为均衡问题来处理,因此它有较为广泛的应用.从上世纪60年代,由Lions,Browder,Ky Fan,Stampacchia等人提出和创立变分不等式与相补问题的基本理论以来,经过许多数学家的努力,变分不等式与相补问题的理论与应用,都取得了重要的发展,并日臻完善.近年来,随着向量优化理论的深入发展,均衡问题的研究由数值函数发展到更为一般的向量值映射.近年来,向量变分不等式与向量均衡问题成为很多数学工作者关注的研究课题(见文献[1-4]及其所附文献).

本文研究一类具有控制结构的强向量均衡问题,利用比较弱的锥连续性与著名的 Fan-KKM定理,得到这类问题解的存在定理,并讨论其解集的性质,改进了文献 [5]的主要结果.

本文安排如下:第二节阐述要研究的问题,并回顾所用到的一些定义与已知结果;第三节给出主要结果及其证明.

2 预备知识

设X,Z是实的Hausdorf f拓扑向量空间,K⊆X是非空闭凸集,P⊆Z是闭凸点锥.P在Z上定义的序关系如下:

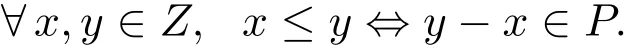
若给定集值映射P:K→2Z,∀x∈K,P(x)是Z中的闭凸点锥,则称集族{P(x):x∈K}是Z上的控制结构,它是Z上的一种变动的序关系[3].给定向量映射f:K×K→Z.考虑下面的具有控制结构的强向量均衡问题(strong vector equilibrium problem with domination structure,简记为:DSVEP):求∈K,满足

如果∀x∈K,P(x)=P(一个固定锥),则(DSVEP)变为下面的强向量均衡问题(简记为: SVEP):求∈K,满足

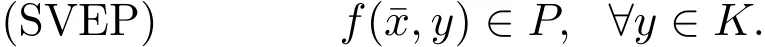
(DSVEP)与(SVEP)就是求向量均衡问题的强解.这是一种理想的解,它比向量均衡问题的其他解,例如:弱有效解,有效解,真有效解等,都更好[3,4,6-12].因此,研究上述强向量均衡问题,讨论其解的存在性与解集的性质,是有意义的.

下面介绍向量映射锥连续的概念.

定义 2.1[12]设f:K→Z,而P⊆Z是闭凸锥.称f在x0∈K是P-连续的,如果对于Z中零元的任何邻V,存在x0的邻域U(x0),使得

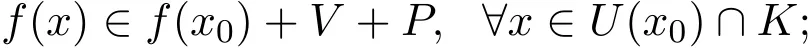
称f在K是P-连续的,如果f在K的每一点都是P-连续的.

注 2.1由文献[12]知,如果f是连续的,则f同时是P连续与−P连续的;反之,当P具有闭凸有界基时,f同时是P连续与−P连续的,才有连续性.因此,与通常的连续性相比,锥连续性是一种较弱的连续性.

定义 2.2[13]设K⊆X为非空凸子集,向量映射f:K→Z.

(i)称f是凸的,如果∀x,y∈K,t∈[0,1],有

(ii)称f是真拟凸的,如果∀x,y∈K,t∈[0,1],有

(iii)称f拟凸的,如果∀z∈Z,集{x∈K:z∈f(x)+P}是凸的;

(iv)称f是凹(真拟凹,拟凹)的,如果−f是凸(真拟凸,拟凸)的.

易见,若f是凸(凹)的,则f是拟凸(拟凹)的;若f是真拟凸(凹)的,则f是拟凸(凹)的.反之,未必成立[13].

用数学归纳法,容易证明下面的引理(也可见文献[5]的引理4.1).

引理 2.1(真拟凸的性质) 设K⊆X为非空凸子集,向量映射f:K→Z.f是真拟凸的

当且仅当∀x1,x2,···,xn∈K,,均存在某个i∈{1,2,···,n},使得

仿上面的定义,引进下面的概念.

定义 2.3设f:K×K→Z,{P(x):x∈K}是Z上的控制结构.

(i)∀x∈K,称f(x,y)关于y∈K 是P(x)真拟凸的,即∀x∈K,∀y1,y2∈K,t∈[0,1],有

f(x,y1)∈f(x,ty1+(1−t)y2)+P(x) 或 f(x,y2)∈f(x,ty1+(1−t)y2)+P(x);

(ii)∀y∈K,称f(x,y)是P(x)连续的,即对于Z中零元的任何邻V,∀x0∈K,存在x0的邻域U(x0),使得

定义 2.4[14]设K是线性空间X中的非空子集,称集值映射F:K→2X是KKM映射,如果对任意的有限集{x1,x2,···,xn}⊆K,有

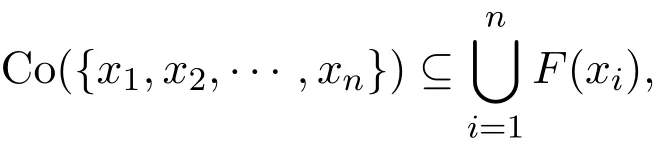
其中Co(A)表示集A的凸包.

下面熟知的Fan-KKM定理是本文的主要工具.

Fan-KKM 定理[14]设K是Hausdor ff拓扑线性空间X中的非空子集,F:K→2X是KKM映射,∀x∈K,F(x)是闭集,且存在x0∈K,使得F(x0)是紧集,则

3 主要结果

最近,文献[5]利用数值化方法研究了(SVEP),得到下面的主要结果,其中的不等式表示的是Z上的序关系.

定理 3.1(文献[5]的定理3.1) 设X,Z是实的局部凸Hausdorf f拓扑向量空间,K⊆X是紧凸子集,P⊆Z是闭的凸点锥,令P的对偶锥P∗有ω∗紧凸基B;映射S:K→2K是一个连续的集值映射,且对每个x∈K,S(x)是非空闭凸集.若映射f:K×K→Z是连续的,且∀x∈K,f(x,x)≥0;而 f(x,y)关于第一变元凹,关于第二变元拟凸,则存在∈K,使∀y∈K,有f(,y)≥0.

关于上述定理的条件,有两点值得注意:

(i)作者在文中,并未给出向量映射拟凸的定义,但仔细检查该定理的证明,从证明中的(2)式与(3)式,可看出作者利用定理中f(x,y)关于第二变元拟凸的条件,实际上是真拟凸,因此定理的这一条件应改为:f(x,y)关于第一变元凹,关于第二变元真拟凸.这样,定理的条件才是确切的,不会引起误解;

(ii)仔细检查该定理的证明,第 444页,第 7行,作者用到条件但在定理3.1中,由现有的条件得不到此结论.现举一简单例子说明.

设X=R(实数全体,赋予通常的线性拓扑),K=[0,1],定义集值映射S:K→2K如下:∀x∈K,令S(x)=.易见S满足定理的条件,但是K的真子集.因此在定理的叙述中,应该加上该条件,否则就不能完成证明.

经过分析与研究,上述定理的条件可简化与减弱、结论可增强,改进为下面的定理(详细证明见后).

定理 3.2设X,Z是实的Hausdorf f拓扑向量空间,K⊆X是非空紧凸子集,P⊆Z是闭凸点锥,映射f:K×K→Z.如果下面条件成立:

(i)∀x∈K,f(x,x)≥0;

(ii)∀y∈K,f(x,y)关于x∈K是−P连续的;

(iii)∀x∈K,f(x,y)关于y∈K 是真拟凸的.

此外,如果添加条件(iv)∀y∈K,f(x,y)关于x∈K是凹的,则问题的解集是K的非空紧凸子集.

比较上面两个定理,可看出定理3.2有如下的改进:

(1)X,Z不必是局部凸空间;

(2)不需要P的对偶锥P∗具有ω∗紧凸基,以及与集值映射S有关的条件.众所周知,对偶锥具有ω∗紧凸基的条件,等价于P有非空的拓扑内部[15],这是一个比较强的条件.因为在很多情况下,例如,经典的Banach空间ℓp,Lp(Ω)(p>1)中的标准序锥,其拓扑内部可以是空集 [15];

(3)不需要f关于两个变元均连续的条件,而用比较弱的、关于第一变元是锥连续的条件代替;

(4)如果仅证明解集是K的非空紧子集,则不需要f关于第一变元凹的条件;如果添加这一条件,则得到解集是K的非空紧凸子集.

事实上,可以得到下面比定理3.2更一般的结果,即讨论具有控制结构的强向量均衡问题(DSVEP)的解.

定理 3.3设 X,Z是实的 Hausdorf f拓扑向量空间,K ⊆X 是非空闭凸集.集值映射P:K→2Z,∀x∈K,P(x)是Z中的闭凸点锥.映射f:K×K→Z.如果下面条件成立:

(i)∀x∈K,f(x,x)∈P(x);

(ii)∀y∈K,f(x,y)是−P(x)连续的;

(iii)∀x∈K,f(x,y)关于y∈K是P(x)真拟凸的;

(iv)映射P上半连续;

(v)存在非空紧凸子集B⊆K,与y0∈B,使得∀x∈KB,满足f(x,y0)/∈P(x).则(DSVEP)有解,即存在∈B,使得∀y∈K,f(,y)∈P(),并且其解集是K的紧子集.

证明定义集值映射F:K→2Z如下:

(I)对任何y∈K,F(y)是K的非空闭子集.

断言(1)式成立.如果(1)式不对,则f(x0,y)/∈P(x0).因P(x0)闭,故由文献[16]的定理3知,存在Z中零元的邻域V,使得

因P(x0)是凸锥,由上式得

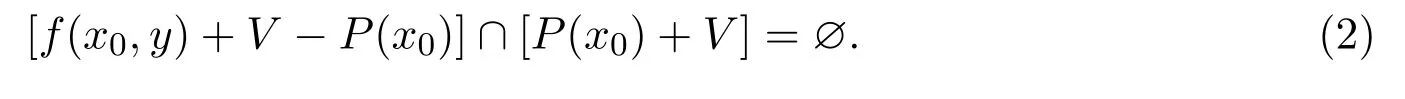
由条件(ii),存在x0的邻域U(x0),使得

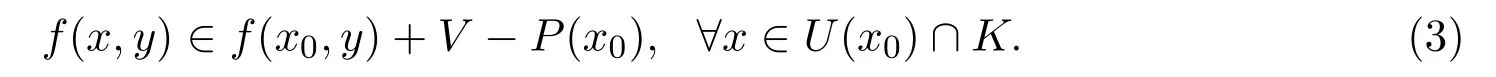
因xα→x0,故存在α0,使得∀α≥α0,有xα∈U(x0)∩K.由(3)式,得

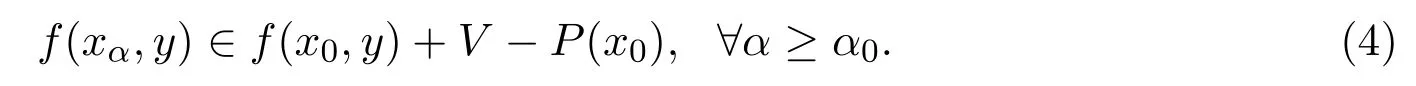
由(2)式和(4)式,得

另一方面,由条件(iv),存在x0的邻域(x0),使得

因xα→x0,故存在α∗≥α0,使得∀α≥α∗,xα∈U(x0)∩(x0)∩K.由(6)式得

由xα∈G(y),得

由(7)式与(8)式,得

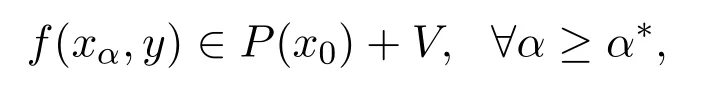
这与(5)式矛盾.

(II)F是KKM映射.

用反证法.若不然,则存在

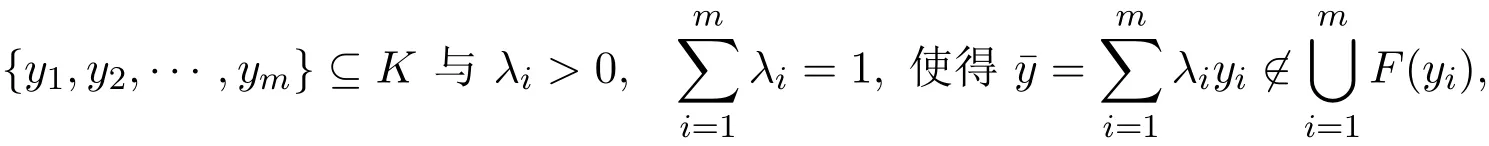
即

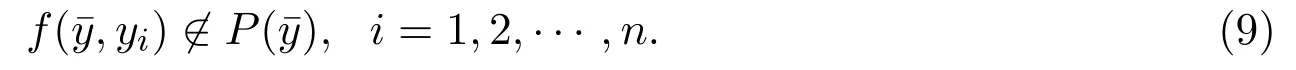
但由条件(iii)以及真拟凸的性质知,存在某个i0,使得

(10)式与(9)式是矛盾的.所以,F是KKM映射.

(III)F(y0)⊆B.

因条件(v),KB⊆KF(y0).已知B紧,又由第(I)段证明知,F(y0)闭,因此,F(y0)是紧的.

定理 3.2的证明在定理3.3中,令P(x)=P,∀x∈K;又令B=K,易见,定理3.3的条件(iv)与(v)均成立.由定理3.3,(SVEP)的解集是K的非空紧子集.

记该解集为 E,并设定理 3.2的条件 (iv)成立,下面证明 E是 K 的凸子集.事实上,设 x1,x2∈E,t∈(0,1),记=tx1+(1−t)x2,要证:∈E.对于任意给定的 y∈K,因x1,x2∈E,所以有

由条件(iv),有

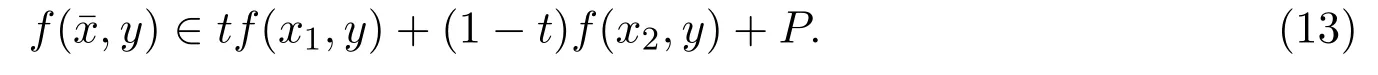
参考文献

[1]张石生.变分不等式和相补问题[M].上海:上海科技文献出版社,1991.

[2]Blum E,Oettli W.From optimization and variational inequalities to equilibrium problems[J].The Mathematics Student,1994,63:123-145.

[3]Chen G Y,Huang X X,Yang X Q.Vector Optimization,Set-Valued and Variational Analysis[M].Berlin: Springer-Verlag,2005.

[4]Giannessi F.Vector Variational Inequalities and Vector Equilibria:Mathematical Theories[M].Dordrecht: Kluwer Academic Publishers,2000.

[5]曹玉茹,郑戟明.拓扑向量空间中的一类平衡问题研究[J].纯粹数学与应用数学,2012,28(4):440-445.

[6]Gong X H.Strong vector equilibrium problem[J].Journal of Global Optimization,2006,36:339-349.

[7]Gong X H.Optimality conditions for vector equilibrium problems[J].Journal of Mathematical Analysis and Applications,2008,342:1455-1466.

[8]Long X J,Huang N J,Teo K L.Existence and stability of solutions for generalized vector quasi-equilibrium problem[J].Mathematical and Computer Modelling,2008,47:445-451.

[9]Hou S H,Gong X H,Yang X M.Existence and stability of solutions for generalized Ky Fan Inequality Problems with trifunctions[J].Journal of Optimization Theory and Applications,2010,146:387-398.

[10]Fu J Y.Generalized vector quasi-equilibrium problems[J].Mathematical Methods of Operations Research, 2000,52:57-64.

[11]傅俊义.强向量均衡问题[J].数学物理学报:A辑,2011,31(4):923-929.

[12]Luc D T.Theory of Vector Optimization[C]//Lecture Notes in Economics and Mathematical Systems. Berlin:Springer-Verlag,1989.

[13]Tanaka T.Generalized quasiconvexities,cone saddle points,and minimax theorem for vector-valued functions[J].Journal of Optimization Theory and Applications,1994,81:355-377.

[14]Fan K.A generalization of Tychonof f′s f i xed point theorem[J].Mathematische Annalen,1961,142:305-310.

[15]Jahn J.Mathematical Vector Optimization in Partially Ordered Linear Spaces[M].Frankfurt:Peter Lang, 1986.

[16]Berge C.Topological Spaces[M].Edinburgh and Lodon:Oliver&Boyd,1963.

Remark on“study of equilibrium problem in topological space”

Fu Junyi,Wang Sanhua
(Department of Mathematics,Nanchang University,Nanchang 330031,China)

Using the cone-continuity of vector mappings which is weaker than the usual continuity,and the well-known Fan-KKM theorem,we prove existence theorems of solutions for strong vector equilibrium problems with domination structure,and discuss the property of solution sets.A main result in the related work is improved.

strong vector equilibrium problem,cone-continuity,domination structure,solution set

O224

A

1008-5513(2014)02-0129-07

10.3969/j.issn.1008-5513.2014.02.002

2013-07-04.

国家自然科学基金(11201216,11061023).

傅俊义(1941-),教授,研究方向:向量变分不等式.

2010 MSC:90C33,49J40