苏彦捷 潘星宇 俞清怡

（北京大学 心理学系，北京 100871）

儿童对数量线性分布规则的理解及其与数量表征的关系

苏彦捷*潘星宇 俞清怡

（北京大学 心理学系，北京 100871）

早期教育中对算术知识的强调可能会影响儿童的数学思维和数学成就。本研究以60名一、二、四年级小学生和10名大学本科生为研究对象，考察算术知识与个体理解数量线性分布规则的关系。数字线估计判断任务的结果发现，随着年龄的增长，个体对线性分布规则的理解方式由基于分类的直觉性理解逐渐转变为基于算术的理解。使用算术理解的儿童在数规律理解和数量表征上都有更好的表现，这可能是因为他们更好地掌握并运用了相关的算术知识。

数量表征；数量线性分布规律；数估计；算术知识

一、引言

数量表征指个体在数字和数字所代表的量之间形成的映射关系。［1］64-88这种映射关系最初是对数形态的，即随着数字的增大，心理量的增长速度小于实际量的增长速度。［2］通过数学学习，个体逐渐理解并内化了数量的线性分布规则（如，0和1之间的距离等同于8到9之间的距离），其数量估计的表征（或数量表征）也由对数形态变为线性形态。［2-5］这种对数量大小及数量线性分布规律的理解是个体进一步数学学习的基础。［6］儿童在数估计［2-3］和数分类［7］任务上的表现及他们的数学成绩［8］都与他们对数量线性分布规则的理解紧密相关。

儿童对数量线性分布规则的理解决定了他们数量表征的形态，其中后者可由数字线估计任务直接测得。［2-4，8-10］在数字线估计任务中，研究者给儿童呈现一条线段，线段的左右端点分别标有两个数字（如0和100），让儿童在线段数轴上估计某些数字（如15）的位置，通过对比儿童给出的估计及其实际数量，来评价儿童的数量表征更接近对数形态还是线性形态。

儿童的数量表征的形态不仅与年龄相关，也受到数量范围变化的影响。［2，11］Siegler和Opferd在西方儿童的研究中发现，在数量范围较小时（如0～100的数轴），幼儿园和一年级儿童做出的数量估计和实际数量之间呈对数关系，在二年级儿童中两者则呈线性关系，即二年级儿童开始使用线性表征；在数量范围较大时（如0～1 000的数轴），即使二年级的儿童也只会使用对数表征。［2］周广东等人在中国儿童的研究中则发现，在0～100的数量范围上，一年级的儿童已能使用线性表征；而在0～1 000的数量范围上，也有半数的一年级儿童可以使用线性表征。［11］中西方儿童的数量表征在由对数形态向线性形态转变的时间点上存在差异，这一跨文化差异可能与中国儿童较早使用测量工具（如直尺等）有关。［12］当然，数量表征发展的文化特点，还需要更多的实证研究结果支持。［13］

（一）基于分类的数量表征

儿童的数量表征形态为什么会随数量范围发生变化呢？有研究者认为，这可能是因为儿童对数量线性分布规律的理解是基于分类的。［7］在进行数量估计时，儿童会采用“分而治之”的策略，首先将数量简单区分为“大数”“小数”两类，再进行之后的操作。当数量范围较大时，由于这个数量分类的过程呈现出对数模式，最终数字线估计的结果也就自然呈现对数形态。在此基础上，Ebersbach等人提出，儿童对数量的分类不仅与任务中设定的数量范围有关，还取决于他们自己所熟悉的数量范围，也就是他们可以正确数到的最大数字。当儿童看到一个数字时，会内隐地将其归为自己“熟悉”或“不熟悉”的。在熟悉范围内，儿童的数量表征呈线性形态；而在熟悉范围之外，数量表征形态则会发生变化。［14］

这种“基于分类”的理解，可能导致个体的数量表征受到数量范围的影响。事实上，除了数量表征，其他一些数学能力也受到了数量范围的影响。以计数能力为例，许多儿童计数能力研究都发现了“数量范围限制”现象。比如，3至5岁的儿童在计数过程中首先能够区分1、2和3［15］179-201，［16］；掌握“数到的最后一个数就表示总数”这一规则后，他们就可以用这种方法正确数出大于3的数［17］，并能够进行进位［18］，但他们的言语计数能力仍受到数量范围的限制［14］。而这种“数量范围限制”并不会出现在成人的计数过程中，个体一旦掌握并理解了计数的规则（一个数n的下一项就是n+1），就可以构造出无限长的计数序列。由此可见，掌握相应算术知识（arithmetic fact）对计数能力起到了关键的作用，尤其是对“数量范围限制”的影响。那么，儿童数量表征形态受数量范围的影响，是不是也和他们掌握的算术知识有关呢？

（二）基于算术的数量表征

随着儿童的数学学习和算术运算练习，他们掌握的算术知识不断累积，建立并强化了简单运算与结果之间的联系，进而在数量表征上也发生了质的变化。［19］比如，大多数一年级儿童可以根据加数、被加数与和之间的记忆联系直接提取一位数加法的结果，而无需借助其他策略（如手指计数［20］）。不仅如此，让幼儿园和三年级儿童从三个个位数中选出最相似的两个和最不相似的两个时，他们通常依据数量大小或是数字在计数序列中的相邻关系进行选择，如在3、4和9三个数字中他们会认为3和4较相似，因为“它们都很小”或“4紧跟在3后面”；而在同样的任务中，六年级学生和成人则会依据“奇数”“偶数”或数字间的倍数关系进行选择，他们认为3和9较相似，因为“它们都是奇数”或“9是3的倍数”。［19］

在数量分类的过程中，这些算术知识可被用于修正数量分类的结果。例如，6～7岁儿童可能直觉性的认为“27”是一个“大数”，在0～50数量范围中这是正确的分类［7］；但在0～100数量范围中这就是错误的分类，此时算术知识就能够起到修正作用：算术知识提示儿童，27与0之间的距离小于27到100的距离，儿童可以据此来为“27”找到合适的位置。与直觉性的分类不同，算术知识的普适性可以帮助儿童在不同的数量范围上都做出合理的、线性的估计。如果以上假设成立，那么除了基于分类的数量表征，可能还存在一种基于线性规则理解的、即基于算术的数量表征；随着儿童逐步掌握算术知识，他们的数量表征方式就会从基于分类的转变为基于算术的。

由此可见，儿童究竟是使用基于分类还是基于算术的数量表征，很大程度上与他们所掌握的算术知识有关。只有在算术知识易得（即个体对算术知识可以熟练提取）且正确（即个体内隐或外显的认为自己提取出的算术知识是正确的）时，基于算术的理解才会占据主导地位；否则，个体会继续沿用直觉化的分类理解。考虑到中国儿童在早期教育中就接受了很多的算术训练［21］，［22］163-207，且在小学阶段就很好地掌握了算术技能［23］2022-2024，［24］59-84，［25］19-29，因此他们可能已经具有了足够的算术知识，并使用基于算术的数量表征。

（三）研究问题和假设

数量表征的可塑性得到了越来越多的数据支持［26］，也为我们更好地理解教育和文化的影响提供了条件。在以往研究的基础上，本研究试图以中国儿童为被试，探索除了对数量线性分布规则的“基于分类”的理解之外，是否还存在一种对该规则的“基于算术”的理解；并考查熟练掌握并内化算术运算规则，是否是儿童形成“基于算术”的数量表征方式的先决条件。由于在中国儿童中，算术是小学低年级阶段（1～3年级）的主要学习任务；亦有研究发现，7～10岁儿童的数表征方式发生了显著变化。这表明7～10岁（1～3年级）可能是数量线性规则理解和数量表征发展的关键时期。由此，本研究选取了一二四年级小学生为研究样本，并选取了大学生作为成人参照。

要考查儿童对数量线性分布规则这一概念性算术知识的理解，就需要考虑到程序性知识（即在具体情境中“如何做”的知识）和效用性知识（即“在哪些情境中应用”的知识）的可能混淆。［27］有研究者提出，让儿童对自己的问题解决过程做出言语描述和解释，就可以有效测量其对概念性知识的理解。［28］75-110基于此，本研究结合经典的数字线估计范式［2-3，8-10］创设了数字线估计判断任务。在这个新的任务中，实验者向儿童展示他人的数字线估计结果，要求他们从中选择一个最佳结果并给出自己的解释。研究预期，基于算术知识理解数量分布规则的儿童和成人一样，将会更多的使用基于算术的解释，如使用减法并比较得数；而基于直觉性分类来理解数量线性分布规则的儿童，则会更多使用直觉性的解释，比如将某个数字划分为“大数”或是“小数”。这一假设将通过实验1来进行检验。

实验2的研究目的，在于验证儿童的算术知识与其理解线性规则的方式之间的关系。如果对算术知识的掌握程度是儿童具有不同理解方式的原因，那么具有不同理解方式的儿童就会在算术任务（如寻找数字排列规律）中表现出差异，而在对具体数量的直觉判断（如猜测圆盘中珠子的数量）上则没有显著不同。

实验3则考查对数量分布的线性规则有不同理解的儿童，是否会在数量表征上也存在相应的差异。研究使用了两种数字线估计任务，一种数字线估计操作任务；另一种则是更为抽象化的分布判断任务。因为任务中没有提供真正的数轴，所以儿童在此任务中缺乏数量分布中视觉空间的信息，并只能够使用自己的数学知识和对数量线性的理解来完成。实验3假设，儿童在数量线性理解上个体的差异会导致他们在这两个任务上的表现也不同。

二、实验1 个体对数量线性分布规则的理解：基于分类还是基于算术？

（一）被试

60名学龄儿童和10名大学生。其中学龄儿童来自某中部省份的一所外国语小学，包括一年级学生20名（年龄M=7.25，SD=0.48；女生10名），二年级学生20名（年龄M=8.17，SD=0.31；女生10名），四年级学生20名（年龄M=9.95，SD=0.63；女生10名）①这60名儿童即为实验2、3的所有被试。；大学生均来自北京某高校（年龄M=21.33，SD=1.53；女生3名）。

（二）实验任务与程序

数字线估计判断任务。在儿童版任务中，儿童会看到两条彼此平行的20cm线段，线段左端标有0，右端标有1 000。在每条线段上另标记有12个数字，其中一条数轴上数字的位置符合线性分布，另一条则符合对数分布；并在两条线段边上分别画了两种小动物（如图1）。实验者告诉被试，小动物正在学习估计，需要在数轴上标记出数字的大概位置。请被试选择出他们认为位置标记更正确的小动物并解释原因。成人版任务与儿童版基本相同，但并没有小动物图案及故事情境。全部被试参与这一实验，由两名女性实验者对被试进行单独施测，记录被试的选择和解释并编码。

图1 数字线估计判断任务示例

（三）编码

以往研究［19］使用非层次聚类法（non-hierarchical clustering analysis）分析了儿童和成人在数字相似性判断中所使用的标准，并得出以下几个类别：1）算术关系，又包括加减关系和乘除（倍数、约数）关系；2）大小分类；3）无稳定标准。基于以上结果并结合本研究的结果，将被试在任务中给出的解释分为4种类型：

（1）基于算术的解释：考虑算术关系。被试以算术关系为基础进行判断，并使用正确的计算对他们的答案进行了合理化的解释。例如：“91减12是七十几，比12减0的结果大，所以91与12之间的距离应该比0和12之间的距离长”，“这两个数字之间的差小于100，但是如果另两个数字相减大于100，所以后两个数字之间的距离应当更大”等。

（2）“参照单一数字”的解释：提及单个数字的位置。被试使用了单个数字的位置来支持其判断，只是简单的指出某个数字所标记的位置不正确。当主试追问原因时，被试无法给出进一步的解释，或只是简单的将数字归类为“太大”或“太小”。例如：“这个小猫的12标得不对，12应该更靠近左边因为12很小”等。

（3）“参照全局”的解释：提及整体分布。被试给出如“小猫的估计更加分散”这样的解释。当问及缘由时，他们无法给出进一步的解释或者只能说出“因为这些数字之间距离很远”，或“有些数字很大，但是有些数字很小”。

（4）其他解释。其中两名四年级儿童使用了他们自己有关测量的知识来帮助他们判断，但并非有效的算术知识，因而该种解释未被分入“使用算术比较”这类。其中一位儿童认为数轴上的1就等于1mm，他也试图使用算术计算来得出两个数字之间的距离，但在计算过程中出现了错误（1 000-978=13），并且坚持这个错误的回答；而另一位儿童则认为数轴长30mm，并且告知主试他知道应当划分数轴，但是不知道应该如何去做。

由于被试可以同时使用几种不同的解释，研究者记录并分别编码了每一种解释，将能够使用算术比较的儿童记为“基于算术的理解”，而将只能够使用“提及单个数字的位置”或“提及整体分布”的儿童记为“基于分类的理解”。两名实验者彼此独立的进行编码，编码一致性系数α=0.94，经过讨论后，实验者在分歧项目上最终达成了一致意见。

（四）结果与讨论

在数字线估计判断任务中，10名成人被试都只使用了基于算术的解释。而在儿童中，有10名儿童被归类为“基于算术的理解”，47名儿童被归类为“基于分类的理解”，另有3名一年级儿童未能给出一种解释故没有归入这两类中。

任务中一些儿童同时给出了多种解释，31人次使用了“参照单一数字”的解释；31人次使用了“参照全局”的解释；10人次使用了算术来解释支持自己的判断（见表1）。单因素方差分析结果发现，不同年级的儿童在给出解释的数量上存在显著差异，F（2，57）=3.73，p=0.03，η2partial=0.12；事后检验（Bonferroni）显示，这一差异主要表现在四年级儿童提出的解释数（M=1.45，SD=0.69）显著大于一年级儿童（M=0.95，SD=0.51），p=0.03；但两者均与二年级儿童（M=1.20，SD=0.52）没有显著差异，p>0.10。

表1 儿童对数量线性分布规则的解释（N =60）

这一结果显示，在学龄儿童中，确实存在对数量线性分布规则的多种形式的理解。一方面，一些儿童使用了基于单个数字的位置或是基于数字系列的整体分布的解释，在进一步追问时，他们通常使用“大数”“小数”这样的简单分类，因而表现出的是一种“基于分类”的理解，这与以往的研究结果一致。［7］另一方面，更值得注意的是，在一些儿童和全部成人中还存在一种“基于算术”的理解，他们使用算术知识来理解数量线性分布，而不是依靠对数量大小的简单分类。当然，本研究所使用的依赖言语解释的编码系统，可能低估了儿童对数量线性分布的基于算术的理解，即存在一些实际上运用了算术知识的儿童，由于受到言语的限制，未能给出“基于算术”的言语解释。尽管可能存在这样的低估，实验1中仍发现一些使用算术知识来进行估计判断的儿童，这一结果可以为“基于算术的理解”的存在提供较强的佐证。

因此，实验1的结果说明，确实存在一种对数量分布线性规则的基于算术的理解，其表现为个体能够运用算术规则来指导数量关系判断的过程，且能够意识到该过程并进行言语报告。为了进一步验证儿童的算术知识与其对数量分布线性规则的理解方式之间的关系，我们进行了实验2。

三、实验2 不同的线性规则理解方式与儿童算术知识的关系

（一）实验任务与程序

数规律任务。首先，主试向儿童展示画有房子和院子的图片，在它们下方还有一些空着的圈或框。随后，邀请儿童和自己一起在院子里种花和种树，其中绿珠子代表树，红珠子代表花，花和树按照一定规律依次排列的。接着，主试告诉儿童自己已经先种好其中的一部分，让儿童寻找其中的规律，并按规律用珠子种完剩下的花和树，即将珠子填入空白的圈或框中。不同的图片中已经放好的珠子分别满足一定的数字规律，其中包括递增序列、递减序列、双向变化序列、斐波那契数列。在每个序列中，若儿童填入正确并说出了规律，则记为1分，否则记为0分，任务总分为4分。

直觉判断任务。在有参照的情况下，让儿童估计白色圆盘中彩色珠子的数量，其中圆盘和珠子的直径分别为20cm和0.12cm。首先，主试邀请儿童一起玩一个珠子游戏，并让儿童挑选自己最喜欢的颜色。随后，主试取出一包（共80粒）该颜色的珠子倒入圆盘中，向儿童展示后，用挡板遮住。之后，主试另取出20颗同色珠子放入另一个盘子，并告知儿童这个盘子里放了20粒珠子，再让儿童根据这20粒珠子的样子，猜测另一个盘子里有多少颗珠子。全部儿童由两名女性主试进行单独实验。参考以往的数估计研究［8，29］，以常用的“20%标准”评价估计准确性，即如果估计值在80的20%差异范围以内则计1分，否则计0分。

（二）结果与讨论

如表2所示，使用不同数量线性规则理解方式的儿童，在数规律任务上的表现存在差异。其中，使用“基于算术的解释”的儿童，在该任务上的得分显著高于使用“基于分类的理解”的儿童，t（54）=-4.39，p<0.001。而在数量估计任务上，无论是估计准确性还是估计值的大小，两类儿童的表现均没有显著差异，p<0.10。

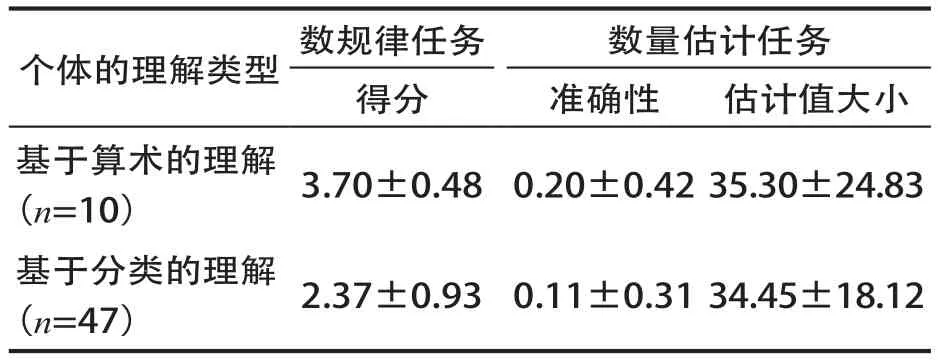
表2 不同的线性规则理解方式对儿童算术、非算术任务表现的影响（M±SD）

在数规律任务上，儿童需要准确的认识不同数字之间的算术关系，因而其问题解决是一个以算术知识为基础的过程。而在数量估计任务上，刺激（珠子）的数量是以非符号形式呈现的，从而不涉及算术线索，并且刺激呈现的时间十分短暂，测量的是个体对实物数量的直觉判断。［30］儿童在这两个任务上的表现出现了分离。这种分离现象提示研究者，儿童对数量线性分布规则的理解方式和他们掌握的算术知识紧密相关，而与他们对数量的直觉无关。

那么，对线性分布规则理解方式不同的儿童，在数量表征上是否也存在差异呢？儿童对线性规则的理解和他们的数量表征之间有怎样的关系？实验3针对这些问题进行了进一步的探索。

四、实验3 儿童对线性规则的理解与其数量表征的关系

（一）实验任务与程序

数字线估计操作任务。主试告诉儿童，小猴为了举办生日聚会而专门准备了一根巧克力棒，要把这个巧克力棒分给来参加聚会的小朋友，并同时向儿童展示一根长100cm的棕色纸棒（模拟巧克力棒），棒上有一个可以移动的指针。儿童需要帮助小猴子，根据目前到场的小伙伴的人数分出相应长度的巧克力棒。

对一年级儿童，主试会告诉他们这根巧克力棒刚好够100个小朋友分，并在纸棒的左右两段分别用卡片标记0和100。对二、四年级儿童，则在纸棒上向他们展示应该给每个小伙伴分的长度（1cm），并在纸棒最左端和距左端1cm处分别用卡片标出0和1作为记号。随后，主试依次向儿童展示12张5cm×5cm的写有数字的卡片（数字在0～100之间，具体刺激见附录），并念出这个数字，儿童则需要通过移动纸棒上的指针来指示应当分出的长度。确认儿童理解了实验任务和操作方法后实验开始，儿童每进行一次操作，主试都会根据纸棒背后的标尺记录下儿童给出的估计值。

分布估计任务。一年级和二年级儿童完成0至200数量范围内的估计任务，四年级儿童完成了0～2 000数量范围内的估计任务。每个数量范围中都包括两个数字系列，每个系列中有10个数字，一个数字系列符合线性分布，另一个系列则符合对数分布。主试告诉儿童，有很多小动物一起排队去参加活动，这些小动物中，有十只小老虎非常淘气，它们一旦彼此靠近就会相互打架。为了维持纪律，老师希望把这10只小老虎排得尽量分散些。如图2所示，每行数字（即一个数字系列）代表一种排法，其中每个数字代表对应的小老虎在队中的位置。儿童需要指出哪种排队方式可以使10只小老虎更分散，并给出解释。

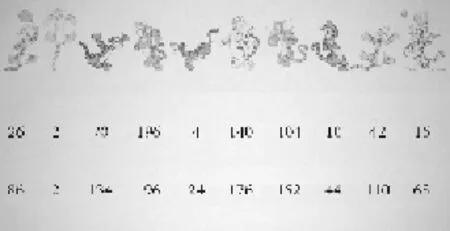
图2 分布估计任务（一、二年级版）示例

（二）结果与讨论

在数字线估计操作中，为检测儿童数字线估计的模式，以实际呈现的数值为自变量，以儿童估计值的中位数为因变量（选中位数而不是平均数作为因变量是为了排除极值的影响），对每一名儿童的数字线估计情况进行线性和对数模型拟合，分别得到他们在线性和对数估计下的模型拟合度R2。分别对各年级儿童的两种模型拟合度进行配对t检验，结果发现各年级儿童的估计结果都更符合线性模型：一年级，MR2lin=0.86 >MR2log=0.75，t（19）=8.43，d=1.98，p<0.001；二年级，MR2lin= 0.87 >MR2log=0.79，t（19）=4.15，d= 0.93，p<0.01；四年级，MR2lin=0.90>MR2log=0.81，t（19）=5.34，d=1.19，p<0.001。

为考查儿童数字线估计的准确性，计算儿童估计值的绝对误差百分比（绝对误差百分比 = |估计值-实际值| /被估计的数值范围）。以绝对误差百分比为因变量，单因素方差分析结果显示表明，三个年级的儿童在估计准确度上并没有显著差异，F（2，57）=2.21，p>0.10，η2partial=0.07。

为考查儿童对数字系统的不同理解与估计表现之间的关系，研究分别比较了“基于算术的理解”和“基于分类的理解”两类儿童的估计模式和估计准确度（表3）。在估计模式方面，使用算术解释的儿童在最优线性拟合函数的拟合度、斜率和截距三个指标上都优于其他儿童：线性函数拟合度更高，t（19.97）=2.12，p<0.05；斜率更大、更接近1，t（55）=2.21，p<0.05；截距也相对较小，t（55）=-1.75，p<0.10。在估计的准确性方面，使用算术解释的儿童在估计操作上的绝对误差百分比小于分类解释的儿童，t（42.37）=-3.02，p<0.01。

表3 儿童对数字系统的不同理解与数字线估计表现之间的关系（M±SD）

在分布估计任务中，给出算术解释的儿童中有60%（6名）选择了线性分布，而在给出分类解释的儿童中也有63.8%（30名）选择线性分布，两类儿童在对线性或对数分布的选择上没有显著差异，χ2（1）= 0.05，p>0.10。

由此可见，在数字线估计操作任务中，可能由于存在可见的数轴与参考点，帮助儿童在数量与空间关系之间建立了直观的对应关系，从而帮助其估计某个数字在数轴上的具体位置。而在新的分布估计任务上，由于没有可见的数轴、各个数量也没有根据数轴的顺序分布，其数量-空间的对应关系更加抽象，任务本身也就更加困难。任务难度的增加可能是导致两类儿童在分布估计任务上不存在差异的原因。根据表征重构理论［31］22-25，只有当儿童熟练掌握并且能够轻松提取、操作算术知识之后，他们才能够使用算术知识来解释自己的问题解决过程。而四年级以及之前的儿童，可能由于掌握的算术知识和熟练程度有限，故而不能顺利完成这一任务。

以上结果说明，对数量线性分布规则的理解方式，可能对儿童在数字线估计操作的表现有重要的影响作用。

五、总讨论

本研究发现，个体对数量分布的线性规则有着多样化的理解，可以根据直觉将数量大致归类为“大数”或者“小数”，也可以借助算术知识来描述数量的相对关系及其分布。前一种理解主要出现在年龄较小的儿童中；而后一种理解被成人广泛使用，但有些学龄儿童也能够使用算术理解方式。对儿童来说，对数量线性分布规则的算术性理解与其灵活使用算术知识的能力有关，使用算术理解的儿童对数量关系更加敏感，并且能准确的将数量关系从具体数字中抽象出来。对数量线性分布规则的理解方式也与儿童的数量表征相关，使用算术理解的儿童在难度适中的任务中能够更准确地表征数量的相对大小。

（一）儿童对数量分布线性规则的理解

过去的研究指出，在完成数字线估计任务时，儿童偏好使用“分而治之”的策略，先将数字大致分为“大数”或者“小数”，再进一步确定数字在数轴上的位置。［7，32］分类在数量理解中是一个关键过程，训练儿童学习正确的分类可以使他们在数字线估计上的表现得到显著提高。［7］实验1中，儿童的言语解释也反映出了这种基于分类的理解，在一定程度上支持了前人的观点，并进一步揭示了分类不仅仅是一个内隐的认知过程，而是可以被言语描述的。更重要的是，在本研究中还发现了另一种不同于分类的理解，成人以及部分儿童能够使用算术知识来指导估计过程，也就是存在一种基于算术的理解方式。这种算术解释与其他两种解释（参照单一点、参照整体分布）在以下两方面有重要差异：1）算术解释中，数字不被分为“小数”或者“大数”；2）通过算术来描述数字之间的关系。

由此可见，中国儿童在小学低年级就已经开始发展出一种对数量线性分布的基于算术的理解。这种“基于算术的理解”不同于“基于分类的理解”，个体开始使用算术知识来帮助理解数量分布规则；但两者也并非完全对立的。实验1的结果显示，尽管在成人中“基于算术的理解”占有主导地位；但在儿童中，尤其是四年级的儿童，普遍给出多种可能的解释，其中既包括“基于分类的理解”也包括“基于算术的理解”。这一结果提示我们，在发展的特定阶段中，儿童对数量分布的线性关系存在多种理解方式；而通过数学学习，基于算术的理解逐渐增多，并可能最终取代基于分类的理解。根据重波理论［33］，由于不同理解在不同情境下各有所长，所以多种理解的共存对发展而言有着适应性的意义。对于较小的数字范围，直觉的、基于分类的理解也符合数量的线性增长规律，当数量范围较大时，这种直觉性的分类就不再准确，而是以一种对数增长的模式发生。除了数量范围的限制外，随着年龄的增长，算术的准确性提高、算术知识的提取变得更容易，也就提供了更加可得、可靠的信息来指导儿童修正其估计。当基于算术的理解最终取代了基于分类的理解时，数字范围对估计模式的影响逐渐消失。然而，要想精确描述儿童对数量关系理解的发展轨迹，还需采用微观发生法来观察发展变化的途径、速度、广度、变异程度和原因。［34］464-510

（二）算术知识、对数量分布线性规则理解与数量表征之间的关系

理解和灵活使用算术知识可能是儿童采用算术来解释数量线性分布规则的重要前提。一方面，只有在掌握了一定的算术知识后，儿童才有可能将其用作自己判断的根据（即算术解释）；在此之前，个体会将数字分为“大数”“小数”而对其数量大小进行简单区分。另一方面，理解算术知识并不是提出算术解释的充分条件。要运用算术知识来解释数量分布的规律，儿童必须首先在二者间建立联系，需要意识到数量线性分布的规则是和相应的算术知识有关的。因此，与那些尚未形成算术理解的个体相比，已发展出算术理解的个体对算术知识的提取（如快速计算出91-12的值）和操作（将算术知识运用在具体情境中）更加容易。这也在实验2中得到了进一步的证据支持，在估计判断中提出算术解释的儿童在数规律任务中表现的更好。他们不仅能够准确识别出递增或递减这样的等差数列，还能够更准确的描述出变化更为复杂的斐波那契数列以及增减混合的双向变化序列。

儿童发展出对数量分布线性规则的算术理解，可能与他们对算术知识的掌握和使用有关。而一旦儿童掌握了算术理解，他们就能够在实际任务中使用这种理解方式来指导其问题解决过程。从实验3的结果看，在数字线估计任务中，算术理解的儿童有更好的表现，而分布估计任务中则不存在这一差异。这可能是由于估计操作与估计判断任务十分相似，唯一的区别在于是自己进行估计操作还是判断他人估计结果的正确性，因此儿童可能在两个任务中使用了相同的策略和算术知识。由此，算术理解的儿童在估计操作任务中，也可能通过给出的数量和标记数量之间的关系来做出估计操作。而在分布估计任务中，所有的刺激都是阿拉伯数字，没有数轴的辅助，并且数量并非根据其在数轴上的顺序排布的。在这种情况下，儿童只能够依靠相应算术知识来解决问题［1］，而没有数轴的辅助，对其工作记忆的要求也相对更高，所以算术理解的儿童并没有在这一任务上表现出优势。

六、结论

对数量线性分布关系存在“基于分类的”和“基于算术的”两种理解。使用算术理解方式的儿童较好地掌握了相关的算术知识，其数量表征形态也更接近线性。从数量关系理解的发展轨迹，以及不同数量关系理解与行为表现之间的联系来看，算术知识的掌握可能促进了由“基于分类的理解”到“基于算术的理解”的转换，而这一转换也可能促进了数学能力的发展，但要探索两者之间的因果关系及其发展进程，仍有待后续的研究支持。

［1］Dehaene S. The Number Sense：How the Mind Creates Mathematics［M］. New York：Oxford University Press，1997.

［2］Siegler R S，Opfer J E. The Development of Numerical Estimation：Evidence for Multiple Representations of Numerical Quantity［J］. Psychological Science，2003，14（3）.

［3］Opfer J E，Siegler R S. Representational Change and Children's Numerical Estimation［J］. Cognitive Psychology，2007，55（3）.

［4］Dehaene S，Izard V，Spelke E，et al. Log or linear? Distinct Intuitions of Number Scale in Western and Amazonian Indigene Cultures［J］. Science，2008，320（5880）.

［5］Ashcraft M H，Moore A M. Cognitive Processes of Numerical Estimation in Children［J］. Journal of Experimental Child Psychology，2012，111（2）.

［6］徐继红，司继伟，周新林，等. 数量估计的研究回顾［J］. 心理科学，2010，33（3）.

［7］Laski E V，Siegler R S. Is 27 A Big Number? Correlational and Causal Connections Among Numerical Categorization，Number Line Estimation，and Numerical Magnitude Comparison［J］. Child Development，2007，78（6）.

［8］Booth J L，Siegler R S. Developmental and Individual Difference in Pure Numerical Estimation［J］. Developmental Psychology，2006，41（9）.

［9］Siegler R S，Booth J L. Development of Numerical Estimation in young Children［J］. Child Development，2004，75（2）.

［10］Siegler R S，Mu Y. Chinese Children Excel on Novel Mathematics Problems even before Elementary School［J］. Psychological Science，2008，19（8）.

［11］周广东，莫雷，温红博. 儿童数字估计的表征模式与发展［J］. 心理发展与教育，2009，25（4）.

［12］莫雷，周广东，温红博. 儿童数字估计中的心理长度［J］. 心理学报，2010，42（5）.

［13］Muldoon K，Simms V，Towse J，et al. Cross-Cultural Comparisons of 5-year-olds’ Estimating and Mathematical Ability［J］. Journal of Cross-Cultural Psychology，2011，42（4） .

［14］Ebersbach M，Luwel K，Frick A，et al. The Relationship Between the Shape of the Mental Number line and Familiarity with Numbers in 5- to 9-year Old Children：Evidence for a segmented linear model［J］. Journal of Experimental Child Psychology，2008，99（1）.

［15］Gelman R，Gallistel C R. The Child’s Understanding of Number［M］. Cambridge，MA：Harvard University Press，1978.

［16］Gallistel C R，Gelman R. Preverbal and Verbal Counting and Computation［J］. Cognition，1992，44（1-2）.

［17］Le Corre M，Carey S. One，Two，Three，Four，Nothing more：An Investigation of the Conceptual Sources of theVerbal Counting Principles［J］. Cognition，2007，105（2）.

［18］Lipton J S，Spelke E S. Preschool Children’s Mapping of Number Words to Nonsymbolic Numerosities［J］. Child Development，2005，76（5）.

［19］Miller K F，Gelman R. The Child’s Representation of Number：A Multidimensional Scaling Analysis［J］. Child Development，1983，54.

［20］Lemaire P，Siegler R S. Four Aspects of Strategic Change：Contribution to Children’s Learning of Multiplication［J］. Journal of Experimental psychology：General，1995，124（1）.

［21］Geary D C，Bow-Thomas C C，Fan L，et al. Even Before formal Instruction，Chinese Children Outperform American Children in Mental Addition［J］.Cognitive Development，1993，8（4）.

［22］Ginsburg H C，Choi Y E，Lopez L，et al. Happy birthday to you：Early Mathematical Thinking of Asian，South American and U.S. Children［G］// Bryant T N P. Learning and Teaching Mathematics：An International Perspective. East Sussex，UK：Taylor & Francis，1997.

［23］Geary D C，Bow-Thomas C C，Liu F，et al. Development of Arithmetical Competencies in Chinese and American children：Influence of Age，Language，and Schooling［J］. Child Development，1996，67（5）.

［24］Marton F，Dall’ Alba G，Kun T L. Memorizing and Understanding：The Keys to the Paradox?［G］//Watkins D A，Biggs J B. The Chinese Learner：Cultural，Psychological，and Contextual Influences. Hong Kong：Comparative Education Research Centre，1996.

［25］Travers K J，Weinzweig A I. The Second International Mathematics Study［G］//Kaiser G，Luna E，Huntley I. Studies in Mathematics Education SeriesⅡ：International Comparisons in Mathematics Education. London：Falmer Press，1999.

［26］Pinhas M，Pothos E M，Tzelgov J. Zooming in and Out from the Mental Number Line：Evidence for a Number Range Effect［J］. Journal of Experimental Psychology：Learning，Memory，and Cognition，2013，39（3）.

［27］Le Corre M，Van W G，Brannon E M，et al. Re-visiting the Competence/Performance Debate in the Acquisition of the Counting Principles［J］. Cognitive Psychology，2006，52（2）.

［28］Rittle-Johnson B，Siegler R S. The Relation between Conceptual and Procedural Knowledge in learning Mathematics：A Review of the Literature［G］//Donlan C. The Development of Mathematical Skills. East Sussex，UK：Psychology Press，1998.

［29］Gandini D，Lemaire P，Dufau S. Older and younger Adults' Strategies in Approximate Quantification［J］. Acta Psychologica，2008，129（1）.

［30］Halberda J，Feigenson L. Developmental Change in the Acuity of the “Number Sense”：The Approximate Number System in 3-，4-，5-，6-Year-Olds and Adults［J］. Developmental Psychology，2008，44（5）.

［31］Karmiloff-Smith A. Beyond Modularity：A Developmental Perspective on Cognitive Science［M］. Cambridge：MIT press，1992.

［32］Opfer J E，Thompson C A. The Trouble with Transfer：Insights from Microgenetic Changes in the Representation of Numerical Magnitude［J］. Child Development，2008，79（3）.

［33］Siegler R S. Emerging Minds：The Process of Change in Children’s Thinking［M］. New York：Oxford University Press，1996.

［34］Siegler R S. Microgenetic Analyses of Learning［G］//Kuhn D，Siegler R S. Handbook of Child Psychology：Vol. 2. Cognition，Perception，and Language. New York：Wiley，2006.

［责任编辑：江 波］

苏彦捷（1964— ），女，北京人，博士，北京大学心理学系教授、博士生导师，主要从事发展心理学研究。

国家基础科学人才培养基金（项目编号：J1103602）的阶段性成果。

B884.1

A

2095-7068(2014)01-0074-09

2014-02-21

*通讯作者：苏彦捷，E-mail：yjsu@pku.edu.cn。