冯 兰，徐 旭

（吉林大学 数学学院，长春130012）

时滞微分方程是一类重要的数学模型，应用广泛，目前已有许多研究结果.如时滞微分方程的数值稳定性分析、时滞微分方程周期解的存在性、唯一性及其数值解的分析等［1－5］.时滞微分方程是复杂的无穷维系统，系统的平衡点经过Hopf分岔可以产生周期解［3］.时滞系统初值定义在一段区间上，因此需要寻找合适的初始函数定位周期解；计算复杂性较高，而高效计算时滞微分方程周期解的方法目前报道较少［6－7］.时滞方程周期解的计算主要有如下几种方法：

1）通过Fourier级数逼近定位周期解［4－5］；

2）通过摄动法近似计算周期解的近似解析表达式［8－11］；

3）打靶法［4，12－13］.

Fourier级数方法的效率较高，但无法确定周期解的稳定性；利用摄动法近似计算周期解一般只针对具有弱非线性项的系统才有效；打靶法虽然可以通过确定Floquet乘子确定周期解的稳定性，但工作量大、效率低.目前讨论时滞微分方程周期解的研究结果较多，但大多数都是定性分析，主要目的是得到分岔周期解的分岔点、周期及用中心流形和规范性理论计算分岔周期解的稳定性.在数值计算时滞微分方程周期解的方法中，Newton－Picard法通过降低Jacobi矩阵中非零元素的个数提高计算效率［4－5］.本文方法与Newton－Picard的思路不同，应用最优化方法求解时滞系统的周期解，提出了用函数拟合方法确定初始函数的方法.结果表明，与工程上常用的通过函数插值方法逼近初始函数的方法相比［4］，本文方法极大减小了计算量，提高了计算效率.

1 时滞方程周期解的计算

考虑如下具有时滞τ的微分方程系统：

其中：x是n维向量；τ≥0表示时滞；φ表示定义在［－τ，0）上的初始函数；F（·）表示n维实值向量函数.设方程（1）的解片段为xt（φ）＝x（t＋θ，φ），这里xt（φ）（θ）∈C（［－τ，0］，ℝn），其中：－τ≤θ≤0；C是［－τ，0］→ℝn的连续函数Banach空间.

时滞方程的初始值定义在一个初始函数φ（θ）（－τ≤θ≤0）上，系统的周期解应满足xT（φ）＝φ，这里T是周期.为了寻找方程（1）的周期T解，先考虑如下Poincaré映射：

这里xT（φ）为定义在［T－τ，T］上的解片段.于是，计算时滞方程的周期解即为寻找映射（2）的固定点φ，使得r（φ，T）＝Pφ－φ＝0.

此外，时滞微分方程的周期解也由周期T决定.注意到周期解的相位漂移也会产生其他周期解，因此为了获得精确的周期，需要补充相条件s（φ，T）＝0消除由于相位漂移而产生的不确定性.根据上述分析，为了求时滞方程（1）的周期解，需要考虑如下方程：

本文将问题（3）转化为求解如下约束最优化问题：寻找初始函数φ和周期T，在约束条件s（φ，T）＝0下，求函数‖xT（φ）－φ‖2的最小值，即

为了求解问题（4），定义惩罚函数：

这里：‖·‖为2－范数；参数σ称为惩罚引子，是一个较大的正常数.于是，把问题（4）转化为无约束最优化问题：

为了寻找快速收敛的无约束最优化方法，假设P＝（φ，T）T是J（φ，T）极小值点的近似，则根据Newton法，下一次迭代的近似解为

这里：▽2J（P）表示在近似解处的Hessen矩阵；▽J（P）为梯度；而

称为Newton方向，是下一步迭代的搜索方向.

方程（1）的相空间是无限维的，在时滞较大的情形下，映射（3）可能会失去紧性.因此，必须在有限维空间［14］下考虑该系统.数值计算时滞方程（1）周期解的第一步是对初始函数φ进行离散化.选择一个网格步长h＝τ／（N－1），定义网格点τi＝－τ＋（i－1）h.用N 个网格点上的值φi（i＝1，2，…，N）近似地逼近初始函数φ.注意离散初始函数时也可使用非均匀网格点，不影响计算效率［15］.

计算时滞方程的周期解就是找到合适的初始函数φ及周期T，在一般打靶法中，通常用函数插值的方法用N个φi值逼近初始函数φ.但当周期解不是强烈吸引时，或者周期解不稳定时，就需要非常多的φi（即N非常大）确保逼近的有效性.而当N非常大时，用Newton法进行优化计算时，需要计算N×N个元素的Jacobi矩阵，计算量庞大.

事实上，对于给定的初始函数值φi，需要从这些数据中抽取蕴含在其中的规律作为真实初始函数的近似，因此通过φi构造的初始函数φ只需能反映φi的变化趋势即可，不必要求初始函数在每个逼近步都精确地通过φi.如图1所示，本文提出用最小二乘函数拟合方法构造初始函数φ，这样构造的初始函数是在能量范数意义下φi的最佳逼近.

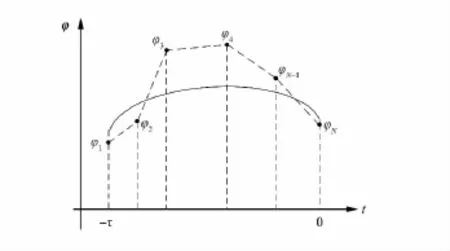
图1 初始函数的构造方式（虚线为经典的（线性）插值方法；实线为本文提出的拟合方法）Fig.1 Construction of the initial function（the dotted line is the figure of classic（linear）interpolation method and solid lines is the figure of fitting method）

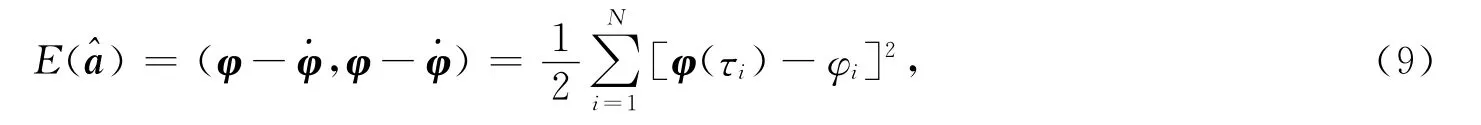
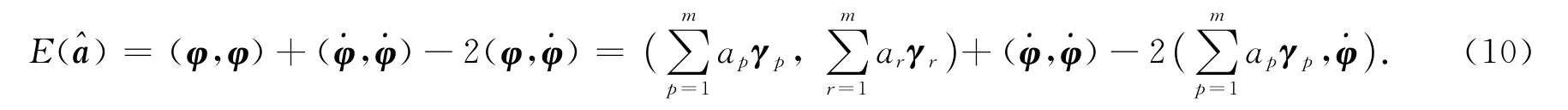
于是，

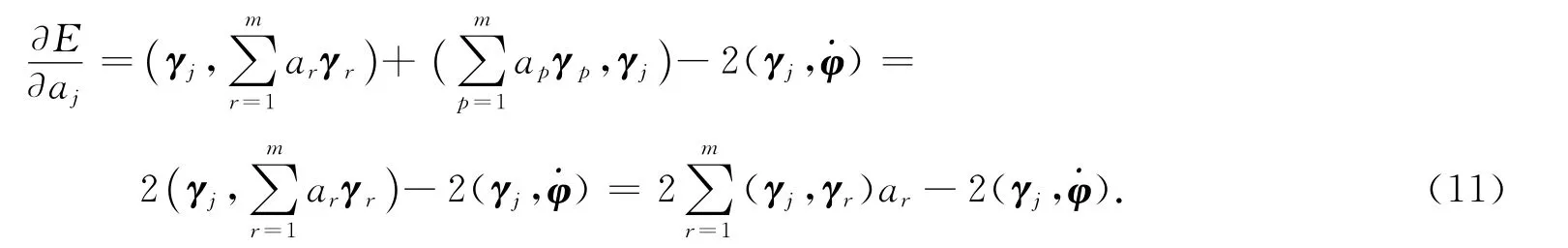
E的最小值满足：

进而有

本文提出的应用最优化方法计算时滞方程周期解的步骤如下：

选取初始数据；给定初始惩罚因子σ＞0，放大系数β＞1，允许误差ε1＞0，ε2＞0.

1）对初始函数φ进行离散化.选择一个网格步长h＝τ／（N－1），定义τi＝－τ＋（i－1）h.

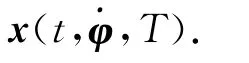
7）保存初始值和周期，迭代结束.

2 数值实验

例1 小世界网络的群体动力学，其运动方程［16］如下：

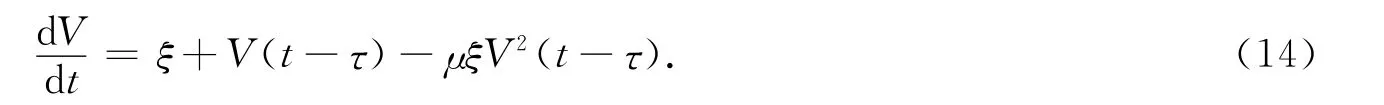
选择ξ＝3，τ＝1，可以计算出μ＝0.040 8，T＝4.应用本文的最优化计算方法，在区间［－1，0］随机选择11个初始函数节点，用3阶多项式作为拟合基函数拟合初始函数.系统的周期选为4，因为周期已知，因此相条件s（φ，T）＝0自动满足.系统的周期解计算结果如图2所示.由图2可见，在［T－τ，T］上的解片段xT（φ）与初始函数φ非常接近，相对误差为

约为0.01%，因此找到了近似周期解.

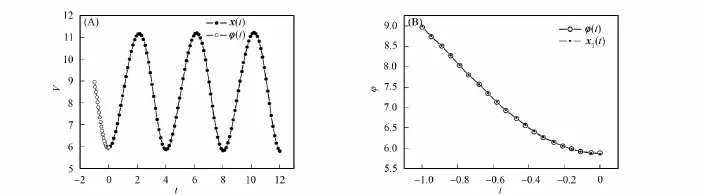
图2 用本文方法计算得到的系统周期解（A）及［T－τ，T］上解xT（φ）和初始函数的比较（B）Fig.2 Periodic solutions（A）obtained by solving optimization problems and the solution segment at［T－τ，T］and the initial function（B）

对于不同的未知数个数（N）及不同的拟合基函数（m），表1列出了计算结果的相对误差.由表1可见：对于相同的拟合基函数m及不同未知数个数N，计算结果的误差几乎相同；而对于相同的未知数个数N，增加拟合基函数的项数m，可以使计算误差减小.但对于3阶或4阶的拟合基函数，计算结果的相对近似约为0.01%，计算精度较高.因此，可以用低阶拟合基函数及较少的未知数获得较好的计算精度.

表1 不同未知数个数与拟合阶的计算误差比较（%）Table 1 Relative error for different unknown variables and fitting orders（%）

例2 考虑系统：

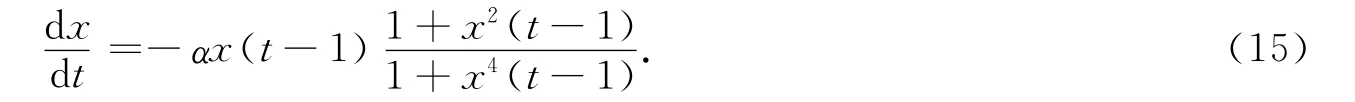
根据文献［15］，当α＝π／2时，系统（15）产生 Hopf分岔；当α＞π／2（并接近π／2）时，系统（15）具有周期为4的周期解.选择a＝1.571，应用本文的最优化计算方法，在区间［－1，0］内随机选择11个初始节点，用4阶多项式作为拟合基函数拟合初始函数，周期选为4，计算所得周期解如图3所示.由图3可见，在［T－τ，T］上的解片段xT（φ）与初始函数非常接近，计算所需的CPU时间为7.405s，计算的相对误差为0.070 2%，因此找到了近似周期解（图3（A））.如果用插值方法逼近初始函数，将［－1，0］区间划分成11个节点（与本文方法未知数个数相同），则系统的计算误差仅为0.267 2%，有较大的计算误差（图3（B））.如果要达到与本文方法相当的误差（约0.07%），通过计算可知，至少需将［－1，0］区间划分成21个节点，计算所需的CPU时间为12.788s，计算量约提升42%.

图3 本文方法（A）与传统方法（B）的计算结果比较Fig.3 Comparison of computational results calculated by the proposed method（A）and conventional method（B）

例3 考虑具有时滞的非线性Duffing振子：

选取k＝0.64，α＝0.36，β＝－0.01，计算可知：当τ＞π（并在π附近）时，系统（16）产生周期为2π的周期解；当β＜0，系统（16）产生的周期解是不稳定的.表2列出了不同方法的计算误差与所用的CPU时间比较.由表2可见，用本文提出的方法，当用3阶拟合多项式时，并不能计算得出周期解；而当m＝5或m＝6时，可以找到周期解，并且计算的误差小于0.01%，表明本文方法对于不稳定周期解的计算有效.如果用传统的线性插值方法计算近似周期解，表2的计算结果表明，当未知数个数为71时，才能找到合适的初始函数，花费的CPU时间为157.213s，远大于本文方法（N＝15，m＝5）需要的CPU时间42.658s，计算时间提升近72.8%.因此本文方法节省了计算量.

表2 不同方法的计算误差比较Table 2 Comparison of computational errors of different methods

综上，本文提出了应用最优化的方法求解时滞微分方程的周期解，考虑了周期解的相位漂移条件，将计算周期解的问题转化为一个具有约束的最优化问题.为了保持Poincaré映射的紧性，求初始函数的有限维逼近，最小二乘拟合的方法通过有限个初始函数值φi逼近真实的初始函数.数值实验表明，用本文的函数拟合方法，用少量的未知数，采用适当阶数的拟合基函数即可获得周期解的初始函数.当周期解的吸引性较强时，采用低阶的拟合基函数即可；当周期解的吸引性较弱或周期解不稳定时，可以采用高阶的拟合基函数得到好的逼近效果.由于在本文提出的方法中，未知数比传统线性插值方法的未知数个数少很多，因此提高了计算效率.

［1］XU Xu，WANG Zai－hua.Effect of Small World Connection on the Dynamics of a Delayed Ring Network ［J］.Nonlinear Dynamics，2009，56（1／2）：127－144.

［2］WANG Zai－hua，HU Hai－yan.Stability and Bifurcation of Delayed Dynamics Systems：From Theory to Applications［J］.Advances in Mechanics，2013，43（1）：3－20.（王在华，胡海岩.时滞动力系统的稳定性与分岔：从理论走向应用 ［J］.力学进展，2013，43（1）：3－20.）

［3］Kuang K.Delay Differential Equations：With Applications in Population Dynamics［M］.New York：Academic Press，1993.

［4］Luzyanina T，Engelborghs K，Lust K，et al.Computation，Continuation and Bifurcation Analysis of Periodic Solutions of Delay Differential Equations ［J］.International Journal of Bifurcation and Chaos，1997，7（11）：2547－2560.

［5］Lust K，Spence A，Champneys A R.An Adaptive Newton－Picard Algorithm with Subspace Iteration for Computing Periodic Solutions［J］.SIAM Journal Scientific Computations，1998，19（4）：1188－1209.

［6］HE Ying－sheng.Numerical Solution and Matlab Simulation of Impulsive Delay Differential Equations［J］.Journal of Jishou University：Natural Sciences Edition，2009，30（4）：30－33.（何迎生.脉冲时滞微分方程的数值解法及Matlab实现 ［J］.吉首大学学报：自然科学学版，2009，30（4）：30－33.）

［7］Minamoto T，Nakao M T.A Numerical Verification Method for a Periodic Solution of a Delay Differential Equation［J］.Journal of Computational and Applied Mathematics，2010，235（3）：870－878.

［8］WANG Wan－yong，XU Jian.Multiple Scales Analysis for Double Hopf Bifurcation with 1∶3Resonances［J］.Nonlinear Dynamics，2011，66（1／2）：39－51.

［9］YOU Xiang－chang，XU Hang.Analytical Approximations for the Periodic Motion of the Duffing System with Delayed Feedback［J］.Numerical Algorithms，2011，56（4）：561－576.

［10］WANG Wan－yong.Resonant Double Hopf Bifurcation and Its Singularity in Systems with Delay Coupling ［D］.Shanghai：Tongji University，2011.（王万永.时滞耦合系统共振双 Hopf分岔奇异性及其分类 ［D］.上海：同济大学，2011.）

［11］ZHENG Yuan－guang.Nonlinear Dynamics of Singularly Perturbed Dynamical Systems with Delays［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2009.（郑远广.含时滞的奇异摄动系统的非线性动力学［D］.南京：南京航空航天大学，2009.）

［12］SHENG Xia，ZHANG Li，ZHENG Hong，et al.Periodic Solutions of a Higher Dimensional Network with Time Delay［J］.Journal of Jilin University：Science Edition，2010，48（5）：728－732.（盛夏，张丽，郑虹，等.具有时滞的高维网络系统的周期解 ［J］.吉林大学学报：理学版，2010，48（5）：728－732.）

［13］FENG Zi－xuan，JI Shu－guan，XU Xu.Finding Periodic Solution of Differential Equation via Solving Optimization［J］.Journal of Jilin University：Science Edition，2009，47（1）：37－39.（冯子玹，冀书关，徐旭.通过求解最优化问题寻找微分方程的周期解 ［J］.吉林大学学报：理学版，2009，47（1）：37－39.）

［14］Küpper T，LI Yong，ZHANG Bo.Periodic Solutions for Dissipative－Repulsive Systems ［J］.Tohoku Mathematical Journal，2000，52（3）：321－329.

［15］XU Jian，Chung K W.Dynamics for a Class of Nonlinear Systems with Time Delay［J］.Chaos，Solitons ＆Fractals，2009，40（1）：28－49.

［16］LI Chun－gang，CHEN Guan－rong.Local Stability and Hopf Bifurcation in Small－World Delayed Networks［J］.Chaos，Solutons ＆ Fractals，2004，20（2）：353－361.