王天营

（南京审计学院 数学与统计学院，南京 210029）

一元线性回归分析中三种检验的等价性研究

王天营

（南京审计学院 数学与统计学院，南京 210029）

在研究两个变量是否线性相关时，要对线性相关系数进行统计检验；在建立线性回归模型时，既要对回归模型中的参数进行统计检验，又要对模型本身进行统计检验。然而，在一元线性回归分析中，尽管对变量线性相关性的检验、模型参数和模型本身检验的目的各不相同，所选统计量也不同，但是，三种检验却具有检验效果的等价性。文章将对此进行研究、证明。

统计量；统计检验；线性相关

在对社会、经济、科技等相关问题进行定量研究的过程中，经常要考察两个变量联系的密切程度及其联系的具体形式，以便通过改变其中一个变量的取值而测定另一个变量的变动，即对两个变量进行相关和回归分析。另一方面，从理论上说，不仅所有非线性回归问题均可以转化为线性回归问题，而且多元线性回归分析的基本机理也与一元线性回归分析的基本机理完全相同。因此，在回归分析中研究最多、最基本的是一元线性回归问题。

1 一元线性回归分析中的三种统计检验

1.1 两变量间线性相关性统计检验

从两变量线性相关及其与回归分析关系看，确立两个变量相关的方向及其联系的密切程度是建立一元线性回归模型的前提，即只有当两个变量存在线性相关关系，或者只有存在高度线性相关关系时，考虑建立两个变量的一元线性回归模型才有意义。所以，当通过样本数据计算出两变量间的线性相关系数之后，通常要对其线性相关程度进行统计检验，即选取适当的统计量，在给定显著性水平下，检验统计量取值的显著性。由此产生了一元回归模型分析中的第一种统计检验——相关系数检验。

假定变量X与变量Y之间的线性相关系数为ρ，-1≤ρ≤1。 通过样本数据(x1，y1)，(x2，y2)，…，(xn，yn)计算变量 X 与变量Y的样本相关系数（即Pearson系数）为

1.2 一元线性回归方程回归系数的统计检验

从一元线性回归方程的建立看，当变量X与变量Y之间存在高度线性相关关系，且进行回归分析时，必须先通过定性分析，在变量X与变量Y之间区分出自变量和因变量。不妨以变量X为自变量、变量Y为因变量，并设它们之间的线性表达式为y=a+bx+ε（为表述方便起见，后文中均用y替代变量 Y，以 x替代变量 X），并假定 ε~N(0，δ2)。 再通过统计调查获得相应的样本数据(x1，y1)，(x2，y2)，…，(xn，yn)，且假定满足条件:

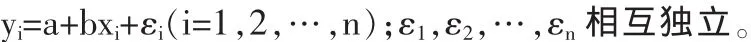
在此假定下，可以推出 yi~N(a+bxi，δ2)，以及 y1，y2，…，yn相互独立。再利用普通最小二乘法（OLS）或极大似然估计法，均可求得线性表达式y=a+bx+ε中参数a，b的点估计为

从而，根据样本数据(x1，y1)，(x2，y2)，…，(xn，yn)求出一元线性回归方程

显然，只要y=a+bx+ε中变量x的系数b≠0，就表明变量x和变量y线性相关。然而，从实际调查的数据来看，对于变量x和变量y的任意一组取值，甚至当变量x和变量y不存在任何关系时，利用式（1）求出参数b的点估计值b赞=0的可能性也非常小。也就是说，一旦通过样本计算出参数b的点估计值b赞≠0，还不能由此推出变量x和变量y真的线性相关，还必须对其作进一步的统计检验。由此产生了一元线性回归模型分析中的第二种统计检——对一元线性回归模型中变量系数（参数）的统计检验。

根据假设检验的基本理论，设原假设与备择假设分别为H0：b=0；H1：b≠0。

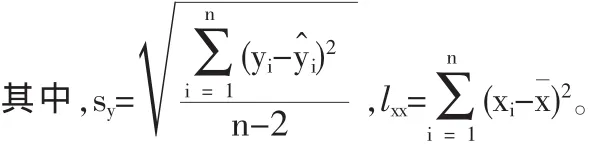
1.3 一元回归模型整体统计显著性检验

从多元线性回归模型，不妨设为y=β0+β1x1+β2x2+…+βkxk+ε，k≥2，对于任意一组样本数据(x11，x21，…，xk1)，（x12，x22，…，xk2），…，(x1n，x2n，…，xkn)，采用普通最小二乘法或极大似然估计法，同样可以分别求得模型中参数 β0，β1，β2，…，βk的点而且它们都几乎不会为零。 也就是说，同一元线性回归一样，必须对模型中每一个变量xi（i=1，2，…，k）的系数（参数）βi进行统计检验。

即假定其它变量取值不变， 检验 H0：βi=0；H1：βi≠0，i=1，2，…，k，并以为统计量，且在 H0：βi=0 为真时，统计量其中，δ赞为多元线性回归分析中的估计标准误差。

但是，在多元线性回归分析中，仅对回归方程中的参数进行独立的统计检验是不够的，还必须对方程本身（或者说把所有自变量看作一个整体）进行统计检验。这是因为即使多元线性回归方程中的每一个自变量均与因变量线性相关，即均能通过单个参数的检验，也并不能保证所选自变量整体对因变量的解释程度显著（或者说也不能保证所选自变量的整体能对因变量作出较为全面的解释）。因此，还必须对因变量与所选自变量的整体间的关系进行检验，并由此产生了第三种检验——一元回归模型整体显著性检验

根据假设检验的基本理论，设原假设与备择假设分别为

选取F=(n-k-1)Sr/Se为检验统计量， 且在H0：β1=β2=…=βk=0 为真时，可以证明：F=(n-k-1)Sr/Se~F(k，n-k-1)。

事实上，对于一元线性回归方程y=a+bx+ε也必须对方程的整体显著性进行统计检验，检验自变量x对因变量y的解释程度如何，它们之间仅仅存在线性相关只是问题的一个方面。为此设原假设与备择假设分别为H0:b=0；H1:b≠0。

选取F=(n-2)Sr/Se为检验统计量，可以证明：在 H0：b=0为真时，F=(n-2)Sr/Se~F(1，n-2)。

由以上不难看出，一元线性回归分析中的三种统计检验，其检验的出发点有着质的区别：相关系数检验是为了检验两个变量之间是否存在线性相关关系，回归方程中变量系数的检验是为了检验单个自变量与因变量间是否存在线性相关关系，方程整体显著性检验是为了检验所选定的自变量作为一个整体对因变量的解释程度。但是，这三种统计检验不仅都与线性相关有关，而且这三个统计量之间还具有相应的数量相等或转化关系。因此，在一元线性回归分析中，它们仅是从不同的角度解决同一个问题，具有检验效果的等价性。但是，对于多元线性回归分析而言，这三种统计检验的效果并不完全相同。

2 一元线性回归分析中三种统计检验的等价性

2.1 线性相关系数与回归系数统计检验的等价性

线性相关系数统计检验与回归系数统计检验的等价性主要体现在如两方面：

（1）在 H0:ρ=0 与 H0:b=0 为真时，统计量与 统 计 量都服从自由度为n-2的t分布。这是这两个检验具有等价性的一个方面，即检验统计量分布的等价性。

（2）可以证明两变量间线性相关和回归系数检验统计量，对于同一样本数据，具有取值上的等同性，即

事实上，对于样本数据(x1，y1)，(x2，y2)，…，(xn，yn)，根据式（1）、（2）及一元线性回归方程y赞=a赞+b赞x，并在 H0:ρ=0 与 H0:b=0都为真时，可得证毕。

由此可见，对于同一样本数据(x1，y1)，(x2，y2)，…，(xn，yn)，统计量的值相同，且均服从自由度为的分布，因此，对两变量线性相关系数的统计检验与对一元回归方程回归系数的统计检验效果完全相同。也就是说，如果两变量线性相关系数能通过统计检验，则相应的回归系数也能通过统计检验；如果两变量线性相关系数不能通过统计检验，则相应的回归系数也不能通过统计检验，反之亦然。由此表明，在解决实际问题时，并不需要既对变量线性相关系数进行统计显著性检验，又对相应的回归系数进行统计显著性检验，只需选择其一进行检验即可。

2.2 回归系数及线性相关系数统计检验与一元线性回归方程整体显著性检验的等价性

（1）可以证明，若随机变量X~t(n)，则随机变量函数Y=X2~F(1，n)。

因为当随机变量X~t(n)时，其概率函数为

将其与随机变量X~F(m，n)的概率函数相比较可知，Y=X2~F（1，n）。这表明自由度为n的t分布可以转化为相应的F分布。证毕。

（2）在一元线性回归分析中，对于同一样本数据有如下数量关系

由此可见，对于同一样本数据(x1，y1)，(x2，y2)，…，(xn，yn)有因此，尽管线性相关系数与回归系数的检验统计量，在相应原假设为真时，所服从的分布与检验方程整体显著性性的统计量所服从的分布不同，但是，如果两变量线性相关系数能通过统计检验，或相应回归系数能通过统计检验，则相应方程整体显著性也能通过统计检验；如果两变量相关系数不能通过统计检验，或相应回归系数不能通过统计检验，则相应方程整体显著性也不能通过统计检验，反之亦然。由此表明，在解决一元线性回归的实际问题中，并不需要既对线性相关系数或相应回归系数进行统计显著性检验，又对相应方程整体进行统计显著性检验，只要在三种统计检验中，任选其一进行统计显著性检验就可达到三种检验的不同目的。

但是，值得注意的是，在多元线性回归分析中，对方程各变量系数（偏回归系数）的统计检验并不能代替对方程整体显著性的统计检验，反之亦然。也就是说，对多元线性回归方程各变量系数（偏回归系数）与方程整体线性分别进行相应的统计检验才能达到不同的目的。

3 验证案例

按照凯恩斯绝对收入消费理论，消费是居民可支配收入水平的函数。消费函数最简单形式为y=a+bx+ε，其中y为居民消费支出；a为居民自发性消费支出，即在收入为0时的消费支出；x为居民可支配收入；b为居民边际消费倾向，即居民可支配收入每改变1个单位所引起居民消费支出的平均改变量。

为研究中国农村居民家庭人均生活消费支出与农村居民家庭人均纯收入之间的关系，本案例收集了1993~2007年中国农村居民家庭人均生活消费支出与其人均纯收入的数据（见表1），并以中国农村居民家庭人均纯收入为自变量、以农村居民家庭人均生活消费支出为因变量，建立1993~2007年中国农村居民生活消费支出一元回归模型。

将上述数据分别代入式（1）、（2）可以求出 1993~2007年中国农村居民家庭人均消费支出对家庭人均纯收入的一元线性回归方程赞=24.5902+0.7575x，以及用于一元线性回归方程系数检验和方程整体显著性检验的统计量t=30.5629，F=934.0876。同样可以求相应时期中国农村居民家庭人均消费支出与其相应人均纯收入之间的相关系数r=0.993113，以及用于变量线性相关性检验的统计量，由此可见

表1 1993~2007年中国农村居民家庭人均生活消费支出与其人均纯收入及计算

而且变量线性相关性与方程回归系数检验的p值为

因此，三种检验的p值相等再一次表明，在一元线性回归分析中，对于同一样本数据和同一显著性水平，三种统计检验的效果具有等价性。其实践意义在于：在有关一元线性回归模型统计检验中，完全不必拘泥于选择哪一种统计检验，任选三种统计检验中的一种均可以做出相同的统计判断。

[1]雷奥奇·卡塞拉（George Casella）(美)，罗杰 L.贝耶（Roger L.Berger）(美).统计推断（英文版·原书第二版）[M].北京：机械工业出版社,2005.

[2]华伯泉.简明数理统计学[M].天津：天津人民出版社，1988.

[3]庄楚强，何春雄.应用数理统计（第三版）[M].广州：华南理工大学出版社，2006.

[4]何灿芝，罗汉.应用统计学[M].长沙：湖南大学出版社，2004.

（责任编辑/亦 民）

O212

A

1002-6487（2011）03-0008-04

王天营（1963-），男，安徽固镇人，博士，副教授，研究方向：统计理论和方法。