高 庚，吴 悠，葛永慧

（太原理工大学 矿业工程学院，太原 030024）

0 引言

在实际生产实践和科学实验中，为了阐明多种因素与事件发生、发展的关系，通常采用多元线性回归分析的方法。多元线性回归研究的是建立一个能反映因变量Y与多个自变量X之间线性关系的多元回归方程，利用这个方程来分析因变量和自变量之间的相互关系，以及回归系数的相关情况等。为了检验回归方程的拟合程度，通常采用复相关系数和复判定系数来进行判定，复相关系数和复判定系数越趋近于1，说明因变量和自变量的线性关系越密切，回归方程的拟合程度越高，回归有效性越好。文献[1]详细叙述了最小二乘法(LS法)在多元线性回归分析中的应用研究，以及相关系数等的计算。文献[2]运用仿真实验的方法，在多元线性回归分析中，通过回归系数估值的相对真误差发现，在应用LS法解算多元线性回归系数时，总会有回归系数估值明显偏离其真值的现象出现，即估值发生了显著漂移。大量模拟实验表明，即便复相关系数和复判定系数都趋近1，也总会有回归系数发生估值漂移现象，甚至会发生严重的估值漂移。在多元回归统计分析的分支中，如主成分分析、因子分析等，回归系数的有效性显得尤为重要，若其回归系数发生了显著估值漂移，则将会产生不可预知的结果。

本文以三元线性回归分析为例，对回归系数中出现的显著估值漂移现象进行了分析与讨论，并进一步通过二元至五元线性回归仿真实验，提出了一种判定多元线性回归系数估值漂移的总体指标和判定回归系数有效性的基本条件。

1 材料与方法

1.1 多元线性回归的计算

多元线性回归方程的一般形式：

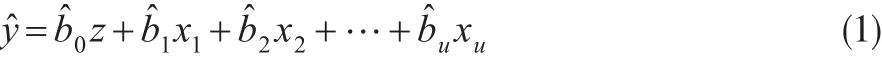
误差方程：

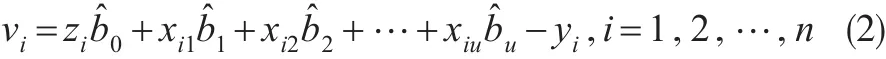
由LS法得多元线性回归的法方程：

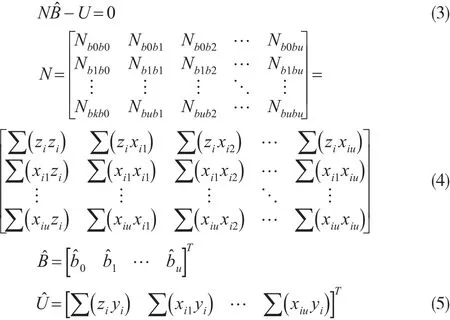
式中，N为法方程系数矩阵，Q为协因数矩阵。

回归系数的解：

观测值的均方误差：

观测值绝对值平均值：

相关系数、复相关系数和复判定系数：

1.2 参数估值的相对真误差与估值漂移

定义：用参数估计方法得到的参数的估值显著地偏离其真值的现象称为参数的估值漂移（Estimated Value Drift，EVD）。当dk＞时就认为是“估值显著地偏离其真值”。不同应用可对赋予不同值。当dk＞=50%时，参数估值的有效数字只有1位，而且还是可疑数字，称为参数具有显著估值漂移。dk表示观测值估值的相对真误差或回归系数估值的相对真误差。

实践表明，在多元线性回归分析中，当观测值母体的均方误差大到一定程度，回归系数估值就可能出现估值漂移现象。用σ0表示观测值母体的均方误差，||表示参与回归计算的观测值绝对值的平均值，ω表示为均方误差系数。对于给定的估值漂移指标，当：

就认为回归系数估值可能产生估值漂移。在实际应用中用观测值的验后均方误差̂0代替观测值母体的均方误差σ0。

2 结果与讨论

2.1 算例

三元线性回归的理论回归方程：

用观测值真值加随机误差生成三组模拟观测值（简称为观测值），三元线性回归的理论观测值与模拟观测值见表1。对于三组模拟观测值分别用LS法计算回归方程回归系数估值、相对真误差及相关系数见表2。

2.1.1 回归系数估值可能产生估值漂移

表1 三元线性回归的理论观测值和模拟观测值

表2 回归系数估值、相对真误差及相关系数

回归数学模型的特点导致了回归系数估值可能产生显著的估值漂移。由于多元线性回归数学模型的特点，导致了用LS法求解时法方程系数间的差异很大，例如在本算例中法方程系数主对角线Nb0b0=10.000、Nb1b1=1.272×1010、Nb2b2=1.808×108和 Nb3b3=2.871×109。不同的观测值误差会导致法方程的常数项有微小的变化，法方程的常数项的微小变化就有可能导致回归系数的显著变化。

观测值估值不会产生显著估值漂移。由后文表3可知，A、B和C三组的观测值估值的相对真误差最大值分别为0.59%、0.29%和0.06%，三组观测值估值与其真值的差异均不显著。

2.1.2 仅用复相关系数和复判定系数说明多元线性回归的有效性有一定局限性

2.2 仿真实验

理论观测值模拟值见表1，仿真实验方法见文献[1]。理论观测值绝对值的平均值约为1500。回归系数估值相对真误差均小于等于给定限值的百分比见表3。回归系数估值相对真误差平均值和相对均方误差平均值的百分比见表4。

表3 回归系数估值相对真误差均小于等于的百分比（%）

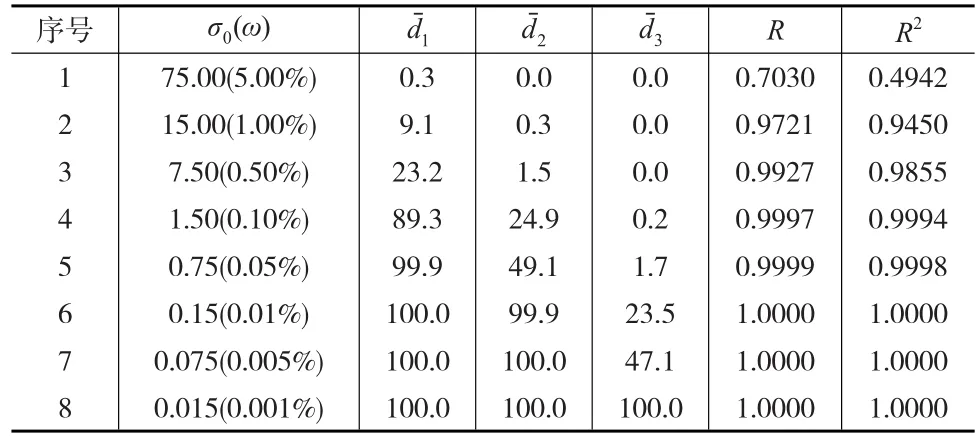
表3 回归系数估值相对真误差均小于等于的百分比（%）

注：σ0表示观测值母体均方误差，ω表示均方误差系数；1表示回归系数估值的相对真误差均小于等于=50%的百分比，2表示回归系数估值的相对真误差均小于等于=10%的百分比，表示回归系数估值的相对真误差均小于等于=1%的百分比。R表示复相关系数的总体平均值，R2表示复判定系数的总体平均值。

序号1 2 3 R R2 0.4942 0.9450 0.9855 0.9994 0.9998 1.0000 1.0000 1.0000 12345678 σ0(ω)75.00(5.00%)15.00(1.00%)7.50(0.50%)1.50(0.10%)0.75(0.05%)0.15(0.01%)0.075(0.005%)0.015(0.001%)0.3 9.1 23.2 89.3 99.9 100.0 100.0 100.0 0.0 0.3 1.5 24.9 49.1 99.9 100.0 100.0 0.0 0.0 0.0 0.2 1.7 23.5 47.1 100.0 0.7030 0.9721 0.9927 0.9997 0.9999 1.0000 1.0000 1.0000

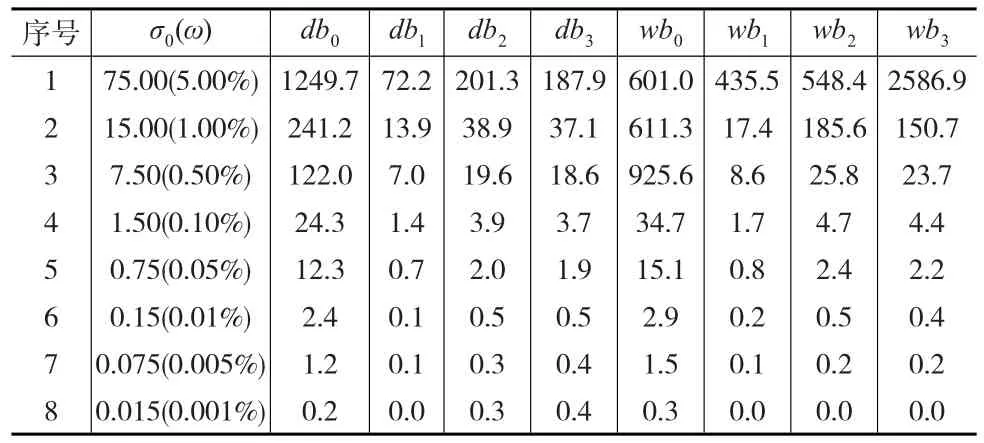
表4回归系数估值相对真误差平均值和相对均方误差平均值的百分比（%）

2.2.1 回归系数估值的估值漂移

由表3可知，当ω=5%时，回归系数估值的相对真误差均小于等于=50%的百分比是0.3%，当ω=1%时，回归系数估值的相对真误差均小于等于1=50%的百分比是9.1%，当ω=0.5%时，回归系数估值的相对真误差均小于等于1=50%的百分比是23.2%，即回归系数估值漂移的显著程度随着均方误差系数ω的增大而增大。对于2=10%和2=1%具有相同的结果。

2.2.2 仅用复相关系数和复判定系数说明多元线性回归的有效性有一定局限性

由表3可知，当ω=1%时，复相关系数和复判定系数总体平均值分别是0.9721和0.9450,回归系数估值的相对真误差均小于等于=50%的百分比是9.1%；当ω=0.5%时，复相关系数和复判定系数总体平均值分别是0.9927和0.9855,回归系数估值的相对真误差均小于等于=50%的百分比是23.2%。由此可见，即使复相关系数和复判定系数满足要求，回归系数的估值也可能产生显著的估值漂移。

2.2.3 回归系数估值的有效性和均方误差系数ω的选取

由表3可知，当ω=0.10%时，回归系数的相对真误差均小于等于=50%的百分比是89.3%；即当ω≈0.10%或ω＜0.10%时，回归系数估值的相对真误差小于等于=50%，回归系数估值具有1位有效数字。当ω=0.01%时，回归系数估值的相对真误差均小于等于=10%的百分比是100%；即当ω≈0.01%或ω＜0.01%时，回归系数估值的相对真误差小于等于=10%，回归系数估值具有2位有效数字。当ω=0.001%时，回归系数估值的相对真误差均小于等于=1.0%的百分比是100%；即当ω≈0.001%或ω＜0.001%时，回归系数估值的相对真误差小于等于=1.0%，回归系数估值具有3位有效数字。

2.2.4 回归系数估值有效性的判定方法

由表4可知，对于相同的均方误差系数ω，回归系数的相对真误差均值和相对均方误差均值的各种百分比均接近。比如，在三元仿真实验中，当ω=0.10%时，回归系数的相对真误差均小于等于=50%的百分比是89.3%，其相对均方误差均小于等于=50%的百分比是88.3%，两者同时小于等于=50%的百分比是82.3%，数据差距不大，对于相同的均方误差系数和其相应给定的限值也具有相同的结果。即用回归系数估值的相对均方误差和用回归系数估值的相对真误差对回归系数估值的有效性判定基本等价，可用回归系数估值的相对均方误差代替回归系数估值的相对真误差对回归系数估值的有效性进行判定。

按照三元线性回归仿真实验的方法，本文模拟了二元至五元线性回归的五组实验，每组至少整理了五个线性回归方程来进行仿真实验，根据每个回归方程观测值绝对值均值来模拟观测值母体均方误差的大小，从而判断回归系数的估值中是否可能会出现估值漂移,并确定判定多元线性回归系数估值漂移的总体指标。对于不同元的线性回归方程，则有不同的回归系数估值漂移总体指标,二元至五元线性回归系数的估值漂移总体指标见表5。

表5 二元至五元线性回归系数估值漂移总体指标(%)

3 结论

多元线性回归中回归系数的估值可能产生估值漂移，随着观测值均方误差的增大，回归系数估值漂移的可能性增大。

在二元线性回归中，当均方误差系数ω≈1.0%或ω＜1.0%时，回归系数估值的相对真误差小于等于=50%（=50%是本文所采用的回归系数估值漂移的临界值，根据不同的应用情况可做适当的调整），回归系数估值具有1位有效数字；当ω≈0.1%或ω＜0.1%时，其相对真误差小于等于=10%，具有2位有效数字；当ω≈0.01%或ω＜0.01%时，其相对真误差小于等于=1.0%，具有3位有效数字。为了确保二元线性回归系数的有效性，至少应当使ω≈0.1%或ω＜0.1%。

在三元至五元线性回归中，当均方误差系数ω≈0.10%或ω＜0.10%时，回归系数估值的相对真误差小于等于=50%，回归系数估值具有1位有效数字；当ω≈0.01%或ω＜0.01%时，其相对真误差小于等于=10%，具有2位有效数字；当ω≈0.001%或ω＜0.001%时，其相对真误差小于等于=1.0%，具有3位有效数字。为了确保三元至五元线性回归系数的有效性，至少应当使ω≈0.01%或ω＜0.01%。

用回归系数估值的相对均方误差和用回归系数估值的相对真误差对回归系数估值的有效性判定基本等价，可用回归系数估值的相对均方误差代替回归系数估值的相对真误差对回归系数估值的有效性进行判定。当回归系数估值的相对均方误差大于50%时，就认为回归系数产生了显著估值漂移。相对于仅用复相关系数和复判定系数确定多元线性回归有效性，增加回归系数估值漂移的确定，对多元线性回归特别是回归系数的有效性确定具有更高的可靠性。